�܂�����
��1�́@���v�����f�[�^�ƌ덷
��2�́@SAS����: �P���W�v
��3�́@�f�[�^�̋L�q�ƕ���
��4�́@���ւƉ�A
��5�́@�N���X�\
��6�́@�����̎菇�Ǝ���: �u�g�D�������̂��߂̏]�ƈ��ӎ������v�}�j���A��
�t�́@CMS����
�Q�l����

�@��w�ɓ���Ɓu���v�w�v�Ȃ�Ȗڂ�����B���������Ă���B���Ȃ�̐l�����C���炢�͂��Ă݂邱�ƂɂȂ�͂����B���������������B�Ƃ��낪�A�����̐l�͎����ɂ͊W�̂Ȃ��ȖڂƑ��X�Ɍ��߂Ă��܂��B�����l���̒��ŁA���̎������ƁA���v�w�������Ŋw�ԋ@��͂��������Ă��Ȃ��̂ɁB
�@������8�N�قǑO�A�������v�w�����̂܂���������Ă������̂��b�B����ƊE�c�̂��璲���̈˗�������A���̉������œ��v���������������Ƃ��������B�������ʂ��܂Ƃ܂�A�����ŏI�Ƃ��������A�������̐搶�͕��ׂŃ_�E���B���ǁA����l�ŕ�����H�ڂɂȂ����B�N���C�A���g�ł������Ƃ̒��������N���X�����A�˂�ψ���ŁA1���Ԕ��قǂł������낤���A�njR�����������I���A�u�������ӌ��E�����ⓙ�������܂��H�v�ƕ����ƁA�^�Ђ̒��������������ނ�Ɏ�������Ď��₵���B�u�搶�����悭���ɂ���w���ցx���ĉ��ł����H �d�������������ł悭�������t�Ȃ�ł����ǁA���܂ł���������ł͈̂��搶����ŁA����ȏ����I�Ȃ��Ƃ͋C��ꂵ�ĕ����Ȃ��������̂Łc�c�B�����͎Ⴂ�搶�Ȃ̂ŁA�ǂ��@��Ɓc�c�B�v
�@�v�킸���ł���B����܂ł�1���Ԕ��͉��������̂��낤�B�����ӋC����Řb���Ă����̂́A���v���Ԃ́u���ցv�W�������̂ł���(�u���ցv�ɂ��Ă͖{����4�����Q�Ƃ̂���)�B���݂����v�w�������Ă��邪�A����͐���E�ԉ��̎p�B���̎��Ԃ͂�����u�o�c�w�ҁv�Ȃ̂ŁA���Ƃ̊Ǘ��E����ɘb������@��͑����B���̂Ƃ����������������A10�l���炢�̊�Ɛl��ɁA���v�w�̘b�𑊊ւȂ瑊�ւƂ����T�O�����ɍi���āA�������m���߂Ȃ���P���Ԃ����ؒ��J�ɐ������Ă�����ƁA�قƂ�ǂ̐l�͂���Ɗ��������ɂ��Ȃ����Ȃ��疞�����ċA���Ă����B����͂���ŋ��t�����ɐs����b�Ȃ̂����c�c�B
�s���P����1: �����I�Ȃ��ƂɂȂ�Ȃ�قǁA�̂��Ȃ��Ă���ł͕����ɂ����Ȃ���̂ł���B���܂�����Ȃ�A�Ȃ��̂��ƁB���ʂ̐_�o�̎���́A�ł��邾�������߂ɁB�t
�@�������������A�p���������v���o������B12�N�O�A�܂���w�@�ɓ����ĊԂ��Ȃ�������̂��ƁA�w�������ɌĂꂽ�B�u�\�Z���c���Ă���̂ŁA��ƑΏۂɌo�c�ɂ��ẴA���P�[�g��������낤�Ǝv���B�N�ɂ܂����邩��D���ɂ���Ă݂Ȃ����B�v���͊�їE��Œ������s���A�Ƃ肠�����P���W�v�����͏I�����B���āA��͉�������낤?
�@���͓��v�w�̐搶�̌������ɑ��k�ɋ삯���B�u�����ł����B����ł͊�{�I�ȂƂ���ŁA����Ȗ{�ł��ǂ�ł݂���ǂ��ł����B�v��3���قnj��o���̂��铝�v�w�̃e�L�X�g���e�[�u���̏�ɕ��ׂ�ꂽ�B��������ǂ��Ƃ̂���e�L�X�g���B�l���Ă݂�ƁA���Ƃ��������Ƃ���܂łɓǂ��v�w�̃e�L�X�g�͌w�ɗ]��ł͂Ȃ����B�������A�����A��w�@�̉��K�ŁA�₽�����Ȑ������v�w�̉p���̐�发�܂œǂ܂���Ă����B�ɂ�������炸�c�c�B
�s���P����2: ���v�w�́A���ۂɎ����Ŏg���Ȃ���A�����Ă����ɂ��Ȃ�Ȃ��B�t
�@���͋C����蒼���āA�����A���ɃR���s���[�^�E�\�t�g�⒲���̓��v�����ŗ��h�ɐ�������҂��o���Ă����F�l���l�ɗ��ݍ���ŁA�R���s���[�^�̓��v�p�b�P�[�W�̎g�����̎�قǂ�������A���v�p�b�P�[�W�̃}�j���A�����蓖�莟��ɓǂ݂�����A��������k���āA���v�w�̐�发��e�L�X�g��ǂݒ������肵�n�߂��B���ɂ��Ďv���A�����ŋ�J���ďW�߂��f�[�^��ڂ̑O�ɂ��āA�悤�₭���p�I�ȃc�[���Ƃ��Ắu���v�w�v���g���K�v�ɖڊo�߂��̂ł��������A���������������w�͂̂������Ȃ��A���ǁA���̒����f�[�^�̉^���́c�c�B
�s���P����3: �ǎ��ȃf�[�^�͐��ł������������������邪�A���̈����f�[�^�́A�ǂ�Ȃɍ��x�ȓ��v��@����g���ė������Ă��A�ƂĂ�������������̂ł͂Ȃ��B�t
�@���v�w�̃e�L�X�g��ǂނƁA�f�[�^�͊��ɗ^�����Ă��邩�A���邢�̓^�_�ł��낪���Ă��邩�̂悤�Ȉ�ۂ���B�������A�ǂ�ȕ���ł���A���ۂ̌����ł́A�ǎ��̃f�[�^���W�߂邱�ƂɘJ�͂̂��Ȃ�̕�������₳���B�f�ނ�O�ɂ��ĉ����ǎ��Ȃ̂������ɂ߂邽�߂ɂ́A�f�[�^���W�̒i�K�Ŋ��ɁA���v�w�����̊ϓ_���痝�����Ă����Ȃ��Ă͂Ȃ�Ȃ������̂ł���B
�@���������̑O�̘b�ł���B���̊ԂɁA���v�w������͈�ς����B�R���s���[�^�Ɠ��v�p�b�P�[�W�̕��y�B�p�[�\�i���E�R���s���[�^�̋��ٓI�����\���B���[�v���E�\�t�g�̐i���ɂƂ��Ȃ��t�@�C���ҏW�\�͂̌���B���܂�A���v�w���g�������v�����́A�قƂ�ǘJ�͂�v���Ȃ��l��ƂɂȂ��Ă���B�������N��I�ɍs���Ă���100�ϐ��~1,000�l���x�̏]�ƈ��ӎ������ł́A���Ȃ蕪�����W�v�\�ł���l�ŏT����2�`3�����g���Ί�������B��̑O�ɂ͂P�`�Q�J���͂������Ă����̂ɁB���v�w�͂��͂�ꕔ�̌����҂̓����I�Ɛ蕨�ł͂Ȃ��B�����Ȃ�Ƃ��m�I�Ȏd��������l�ɂƂ��ẮA�����œ���I�Ɏg����c�[���ɂȂ����̂ł���B�܂�Ń��[�v���̂悤�ɁB
�@����ȓ��v�w�̐V���オ�����J���悤�Ƃ��Ă������ɁA�ꑫ��Ɍo�������Ă����������A�M�d�ł͂��������A������b�̃^�l�ƂȂ��Ă��܂����G�s�\�[�h�����I�����킯�����A�{���͂���ȋ��P�����āA�ʏ�̓��v�w�e�L�X�g�Ƃ͂܂������قȂ�R���Z�v�g�Ɋ�Â��ď�����Ă���B
�@�{���́w�o�c���v����x�Ƒ肵�Ă��邪�A���m�ɂ́u�o�c�w�҂������Ŏg���Ă��铝�v�w�Ɠ��v�p�b�P�[�W�ɂ��ď��������发�v�Ƃ����ׂ��ł��낤�B�����鋳�{���I�ȓ��发�ł͂Ȃ��B���v�w�⒲����@�A����ɃR���s���[�^�ⓝ�v�p�b�P�[�W�̎g�����܂ŁA�c�[���Ƃ��ăp�b�P�[�W�����Ă��܂����Ƃ������z���琶�܂�Ă������v�w���[�U�[�̂��߂̓��发�ł���B�{���ł͍ŏ����瓝�v�w����Ə������͗Z�����Ă��܂��Ă���B���グ������A�f�ނ��A�����g����|���Ă���o�c�w����̒����Ƃ��̃f�[�^����I�ꂽ���̂ł���B
�@���Ȃ��Ƃ����ɂƂ��ẮA10�N�O�̓��v�����ƌ��݂̓��v�����Ƃł́A�����Ă���Ӗ����[�݂��S���قȂ�ʂ̂��̂ł���B�]���́A�����Č��݂ł��命���̐l���M���Ă��铝�v�����ł́A��ςȎ��ԂƘJ�͂𒍂�����ŁA���v�w��R���s���[�^�̐��ƁE�o���҂��������`�[���Œ����A�W�v���s���A�W�v���ʂ���̂Ƃ��������܂Ƃ߂���B�قƂ�ǂ̒����͂�����������ŁA�������A�W�{�덷�̕]���͑����s���Ă��Ă��A�����̃v���Z�X���̂��甭�������W�{�덷�̊Ǘ��͂قƂ�Ljӎ�����Ă��Ȃ��B���v���͂Ƃ͖�����ŁA�قƂ�nj덷��ǂ�ł����悤�Ȃ��̂ł���B
�@�Ƃ��낪�A�����ɂ����ẮA���͂ⓝ�v�I�ȏW�v�����́A�����v���Z�X�S�̂̐܂�Ԃ��u�_�v�ɂ����߂��Ȃ��B�W�v�������̂́A��l�ŁA�����Z���Ԃ̂����ɍs�����Ƃ��o����B�W�v�̓S�[���Ȃ̂ł͂Ȃ��A������Ƃ������ጤ�����s�����߂̒T��j�Ƃ��Ă̖������ʂ������ƂɂȂ�B�������A�R���s���[�^�E�e�N�m���W�[�̐i���́A�S���������\�ɂ��A�x���ꑁ����o�c�w����Łu�W�{�����v�u�W�{�덷�v�Ƃ��������t������ɂ��邾�낤�B�����ł́A��W�{�덷�̊Ǘ�����������ƍs����ׂ��Ȃ̂ł���B
�@���v�����Ƃ͎����ɓ������邽�߂̎�@�ɂق��Ȃ�Ȃ��B���͂��͂�W�v�\�Ŗ��������ɖ��߂���悤�Ȃ��Ƃ͂Ȃ��A���v�����̑O��A���Ɍ�ɍs��ꂽ�q�A�����O�����⎖�ጤ���ɂ���ē���ꂽ�m���Ɉ��Ă���B���������v������1�����̂��̂ł͂Ȃ��A���N�J��Ԃ��J��Ԃ��s����ׂ����i�̂��̂ł���B�����̌���͕K���ǎ����s����ׂ��ł��邵�A���N������V�N�Ȏ��������́A���X�ƐV�������_�≼����A���I�ɐ��ݏo���Ă����B�����ɂ́A�����Ƙ_���̗��ݍ����̒��ŁA�����E���͂����鑤�̃I���W�i���e�B�[����ɋ��߂��Ă���̂ł���B�M�����̍������ጤ�������悤�Ƃ���Ȃ�A���܂ⓝ�v�����͋��͂Ȏ�@�Ȃ̂ł���B
�@���̂��Ƃ͓����ɁA�g�D�J���A���{�I�ɂ����A�g�D�������̐V�����n�����J�����̂ł���B�g�D�̍ĊJ���̂��߂ɂ́A���邢�͐^�̖��_��I�m�ɔc���E�w�E���邽�߂ɂ́A�Г��I�ɂ����v�����̗��t�����K�v�ɂȂ�B�Г��ł̐��|�_��r����ɂ��A��͂蓝�v�����̖��炩�ɂ��鎖�����K�v�Ȃ̂ł���B���̈Ӗ�������A�{���Œ����̎���Ƃ��Ď��グ���u�g�D�������̂��߂̏]�ƈ��ӎ������v�̃m�E�n�E�́u���v�I�g�D�������v�̉\���������Ƃ����Ӗ��ŁA��Ƃ̒S���҂ɂƂ��ėL�v�Ȃ��̂ƂȂ낤�B����́A��w�̌����҂��o�c�g�D�̓��v�������s���ۂɂ��A�K����q���g�ɂȂ�͂��ł���B
�@�{���́A��w�̊w���y�ё�w�@�ɂ�����u�`�m�[�g�����Ƃɂ��č쐬����Ă���B���̍u�`�m�[�g�́A���Ƃ��Ƃ�1988�N�x�Ɋw�K�@��w��w�@�o�c�w�����Ȃɂ����Ĕ��u�t�Ƃ��āu���v�����_�v��S���������Ƃ����������ƂȂ��ď����n�߂�ꂽ���̂ł���B�����ɁA�����������Ă������k��w�o�ϊw���o�c�w�ȂŁA�u�o�c�w�v�[�~�i�[���̊w���w���Ώۂ̑��Ƙ_���w���ɂ�3�N�قǎ�������Ȃ���g�����B���̌�A1991�N�x����A���̏�����������w���{�w���Љ�Ȋw�Ȃɕς���āA�u���v�w�v�u�Љ���@�v��S�����邱�ƂɂȂ����̂ŁA���̍u�`�m�[�g�̉���������ɑ�����ꂽ�̂ł���B���̊ԁA(��)���{���Y���{���̌o�c�A�J�f�~�[�ŁA��Ƃ̎����S���ґ���ɍu�`����ۂɂ��A���̍u�`�m�[�g�̈ꕔ���g�p����Ă����B
�@�{���́A���̐��藧�����炵�āA���ɑ����̕��X�̌�w���A�䏕�͂Ɏx�����Ă���B�܂����̏������铌����w���{�w���Љ�Ȋw�ȓ��v�w�����̑�X�̐搶������͗l�X�Ȍ`�ł����b�ɂȂ����B���ɁA��w�@���ォ���w�������������A�{���̎��M�����߂Ă��������������]�搶�ƁA���莞�ォ���w�������������Ă���ю���搶(���݁A�����w�@��w����)�ɂ́A���̏�����肵�ĐS������\���グ�����B���搶�Ƃ̏o����Ȃ���A�������̂悤�ȃe�L�X�g�����M���邱�Ƃ͂��肦�Ȃ������ł��낤�B
�@�܂��{���̂��ƂɂȂ����u�`�m�[�g���쐬���邫������������Ă����������A�����̊w�K�@��w�����A���݂͒}�g��w�����͍̉����F�搶�B�{���̒��Œ����̎���Ƃ��Ď��グ�Ă���u�g�D�������̂��߂̏]�ƈ��ӎ������v�̎��{�ɁA1986�N�ȗ��A���N�e�g�ɂȂ��ċ��͂��Ă���������(��)���{���Y���{���̐V���v���BSAS�Ɋւ���ŐV�������������Ă�����������SAS�C���X�e�B�e���[�g�W���p���̒|�����b����B�����āA�Y��Ă͂Ȃ�Ȃ��̂́A���k��w�ݐE���ɁA����SAS���[�U�[�Ƃ��ēƂ藧������̂𑽕��ʂ���T�|�[�g���Ă��ꂽ���k��w�������Z���^�[�̃X�^�b�t�̕��X�B�{���̎��M���I�n�g������܂��Ă���������������w�o�ʼn�̏��r�����F���B�����̕��X�ɂ́A���̏�Ŋ��ӂ̈ӂ�\�����Ă������������B
1992�N9��
�����L�v
�@�{���ł́A���v�p�b�P�[�W�Ƃ���SAS(�T�X�Ɠǂ�)�����グ�Ă���BSAS�͂��܂��\�I�ȓ��v�p�b�P�[�W�ł���A�����̑�w�A��Ƃ̑�^�ėp�v�Z�@(��������C���t���[��(mainframe)�ƌĂ�)�Ɋ��ɓ�������Ă���B�܂��p�[�\�i���E�R���s���[�^�p�͂��Ƃ��Ɨ����ŁA���[�v���E�\�t�g���̗����ݒ�i�����������^���j�ł����ɁA�T�C�g�_������Ԃ��ƂŁA1�䓖��̒P�ʉ��i��啝�Ɉ��������邱�Ƃ��ł���B���������āA�{���̑z�肷��ǎ҂ɂƂ��ẮASAS���g�p����@��͏\���ɂ���Ɣ��f�����B
�@SAS�Ƃ́A���Ƃ���Statistical Analysis System (���v���̓V�X�e��)�̗��̂��������A���݂ł́A�f�[�^�Ǘ��@�\���̏d�v���������ASAS�������Ȗ��̂ƂȂ��Ă���B���̌��`�́A1966�N�ɕč��m�[�X�E�J�����C�i(North Carolina)�B����w�ŊJ�����J�n����A1976�N�ɂ́ASAS Institute Inc.���ݗ�����A�Ȍ�ASAS�̈ێ��A�J���A�̔��A���瓙���s���悤�ɂȂ����B�ȒP�Ɍ����ASAS�Ƃ̓f�[�^�E�Z�b�g�ƌĂ��t�@�C���ɑ��āA���v�����E���Z�������͂��߂Ƃ���e��̉��H�������s���p�b�P�[�W�E�v���O�����ł���B�e��̓��v�����p�Ƀv���O���������ꂼ��FORTRAN��BASIC�Ȃǂ̌�����g���Ď����ō쐬�A�J���A�ێ����邱�Ƃ́A��ʂɂ͔��ɑ�ςȍ�Ƃł���B���̓_SAS�́A���Ɋ�������Ă��铝�v�p�v���O�����̏W���́A�V�X�e���ł���A���p�҂��K�v�ȃv���O�������w�肷��ƁA�������@�\�I�Ɍ��ѕt���āA���v���������Ă����킯�ł���B
�@SAS�͂��Ƃ���IBM�̃��C���t���[����œ������v���͗p�\�t�g�E�F�A�Ƃ��Ēa�����A���̌�����C���t���[���p�ɐi���𐋂��Ă������A�ŐV�łł����6��(�����[�X6)�ł́A���C���t���[���p�����p�[�\�i���E�R���s���[�^�p�̕��������o����Ă���B�{���ł́A���̍ŐV�ŁASAS��6�ł̎g�����ƃv���O���~���O�ɂ��āA�p�[�\�i���E�R���s���[�^��SAS�A������PC��SAS�𒆐S�ɁAIBM���C���t���[���̑�\�I�I�y���[�e�B���O�E�V�X�e��(operating system ������ OS) CMS�ɑΉ�����CMS��SAS�ɂ��Ă��A����_�Ȃǂɂ����y���Ȃ��畹���Đ������Ă����BPC��SAS��CMS��SAS�̗����𗼓������I�Ɏ��グ��͖̂{�������߂Ă��Ǝv���B����́A�ŐV�łł���SAS��6�łł́A���C���t���[���p���p�[�\�i���E�R���s���[�^�p���Ƃ���C����ŏ�����A�g�p���@�͊�{�I�ɓ����ł���Ƃ������Ƃɉ����āA���㎄���܂߂đ����̐l�X���A�f�[�^�E�T�C�Y��R�X�g�A���p�\���ȂǗl�X�ȗv�������Ă��āASAS�̃v���b�g�t�H�[���Ƃ��Ẵp�[�\�i���E�R���s���[�^�ƃ��C���t���[�����g�������Ă������ƂɂȂ�ƍl��������ł���B�܂����݂ł��ꕔ���C���t���[���Ŏg�p����Ă���CMS��SAS�����[�X5.18�ɂ��ẮA��{�I�g�p���@���T�����Ă������B
�@���Ȃ݂ɁA���͂��Ƃ���IBM�̃��C���t���[���ł�CMS��SAS���[�U�[�ł��邪�A�{���������ɓ����āA�����Ƃ����オ��ȃV�X�e���\���F
�@�������AMS-DOS�����[�X5.00��EMS��UMB���g���Ă��A�܂����������\���Ɋm�ۂł��Ȃ��B�����ŁA���{��t�����g�E�G���h�E�v���Z�b�T�[(FEP)��DOSSHELL�AMOUSE���A�������ɏ풓���Ă��̕���������H���Ă��܂����̂ɂ��ẮAAUTOEXEC.BAT��CONFIG.SYS�̃t�@�C�����炠�炩���ߍ폜���Ďg�p���Ă���BMS-DOS��SAS�����Ƃ��́A���̃������e�ʂ��ő�̐�������̂悤���B
�@�܂�SAS�̃V�X�e���́ABASE SAS��7.8MB�ASAS/STAT��6.3MB�ƍ��v�����14.1MB���̃f�B�X�N���g��(�p�[�\�i���E�R���s���[�^�p��SAS�����[�X6.04�̑S�v���_�N�g�ł�38.2MB�̃f�B�X�N�e�ʂ��K�v�ɂȂ�)�BMS-DOS���̂ł��A�����Ēu����3MB�ȏ�f�B�X�N���g���B�{���Ŏg�p����SAS�v���O�����̗�ł́A164�ϐ��~907����1.2MB�̉i�vSAS�f�[�^�E�Z�b�g�ƌĂ��MS-DOS�t�@�C�����Œ�f�B�X�N�ɏ풓���邱�ƂɂȂ�̂ŁA��Ɨp�t�@�C���̂��Ƃ��l����ƁA�����̏�ł́A�Œ�f�B�X�N20MB��SAS���u���v�p�b�P�[�W�v�Ƃ��ĉғ��\�Ȃ��肬��̃T�C�Y�ł���B���ꂪ���ۂɉғ����邱�Ƃ�����m�F�ł����̂ŁA�p�[�\�i���E�R���s���[�^�p��SAS�̓������l���Ă���ǎ҂́A�n�[�h�E�F�A�I���̍ۂ̎Q�l�ɂ��Ăق����B
�@�{���̎��M�ɂ������đz�肵�Ă���ǎ҂́A���v�w��R���s���[�^���U���Ȃ��w���A�Љ�l�ł���B�����f�ނ��o�c�w���삩��I��Ă���̂ŁA���Ɍo�c�w����̊w���w���E��w�@���A���邢�͊�Ƃ̐l���E����E�\�͊J���Ȃǂ̒S���҂ɂ́A�����������Ă��炦��Ǝv���B
�@�{���́A�����Ƃ��āu���x�v�u����v�ȓ��v�w���_�̗�����ڎw�����̂ł͂Ȃ��B���v�w�A�����A�f�[�^��͂̍l�����A���g�ݎp����̓����邱�Ƃ�ڎw���B���v�w�A�R���s���[�^�̒m���͑O��ɂ����A�����̊�b�ɂ��Ă͓I���i���āA���J�ɐ�������B
�@�{���̖ړI�́A�ǎ҂����璲���f�[�^���W�߁A���瓝�v�w��R���s���[�^�A���v�p�b�P�[�W����g���āA�����f�[�^�͂ł���悤�ɂ��邱�Ƃł���B�ŏI�I�ɂ́A���Ƙ_���E�C�m�_�����x���̘_���A���̍쐬�Ɂu�g����v���v�w�A���v�����@��ڎw���Ă���A���ɁA�Q����ǂ̍����A�R���s���[�^���g���������f�[�^�̓��v�����ɏd�_���u����Ă���B
�@�{���͎��Ȃ�̐V�������v�w����̃R���Z�v�g�Ɋ�Â��ď�����Ă���B��w�Ŏ��Ƃ̃e�L�X�g�Ƃ��Ďg�p����Ƃ��ɂ́A���̂悤�Ȏg�������ł���B
�@�{���͑S�̂Ƃ��Ē��������v���Z�X���\������悤�ɏ�����Ă��邪�B���̈���Ŋe�͂͋��ނƂ��Ă��Ȃ�Ɨ������������Ă���B�e�͂���Ⓑ�߂Ȃ̂͂��̂��߂ŁASAS�̕����������A�K������1���S����ǂ܂Ȃ��Ă��A�K�v�ȕ����������d�_�I�Ɏg�p���邱�Ƃ��ł���B�Ⴆ�A�{������ƂȂǂł��Z���Ԃ̌��C�p�e�L�X�g�Ƃ��Ďg�p����ꍇ�ɂ́A�u���v�E�����T�_�v�Ȃ����1�������J�ɋ�����悢�B�����̕��͌��ʂɐڂ���l�ɑ��ẮA���ϒl�̗��p�Ɋւ��Ă���3�������������Ă��悢�B���ւ𒆐S����4�������A���邢�̓N���X�\�̓ǂݕ��Ɋւ�����5�������������Ă��悢�BSAS�u�K��ł���A��2�����������ނɎg�����Ƃ��ł���B
�@�{���ɂ́A���ۂ̓��v�������܂邲�ƌf�ڂ���Ă���B��6���͂��Ƃ��Ɠ��v�����}�j���A�����Ӑ}���ď�����Ă���̂ŁA�菇�ɂ��������āA�����Ȃ�̊��Œ������s�����Ƃ��ł���B
�@���v�w�́A���Ƃ��Ƒ����̕��삩��̏����Ȏx�����A�ߋ�2���I�ȏ���������č������A��̑�������ɂȂ����w��ł���B���݂̓��v�w�̗���̒��ɂ́A���R�Ȋw�ɑ����闬����Љ�Ȋw�ɑ����闬������邪�A�l�Ԃ̐����̂�����ʂƂ�����Ȋw�����v�w�Ɗւ���Ă����Ƃ����Ă��������낤�B����������A���ۂ̖@�����ɑ���l�Ԃ̂����Ȃ��T���S�����v�w�ݏo���Ă����̂ł���A���v�w�͉Ȋw�̕��@(the grammar of science)�ł���ƌĂ��R���ł�����B
�@�u���v�w�v�Ƃ����p�ꎩ�̂́A17���I�̃h�C�c�̍����w�ɑk��Ƃ�����B�����w�Ƃ́A���ƌ��������̑��̂̋L�q�Ɋւ���w��ł���A����L�q�w�Ƃł��ĂԂׂ����̂ł������B�����A���v�w���w��Statistik (�p��ł�statistics)�́A����Staat (�p��ł�state)�̏���j�I�ɋL�q���邱�Ƃ��Ӗ����Ă���Ƃ�����B�p���statistics�ɂ́A���̂悤�ɁA�W�c��������o���ꂽ���ʓI���Ƃ��Ă̓��v�������w�����v�������́u���v�f�[�^�v�̈Ӗ��ƁA������A���v�f�[�^�������A���͂��āA�W�c�ɂ��Ă̗L�Ӌ`�ȏ��邱�Ƃ���v�ȉۑ�Ƃ���w��ł���u���v�w�v�̓�̈Ӗ�������B��̈قȂ�T�O�ɓ����P��"statistics"���p�����Ă���̂͂��������w���j�I����ɂ����̂ł���B
�@���v�w�Ƃ͉Ȋw����S�̌����ł���A�Љ�Ȋw�̕���ɂ����ẮA�Љ�A�o�ρA�o�c���ۂ��܂߂āA�����̌��ۂ��ǂ�Ȃӂ���(how)�ɂȂ��Ă��邩�ׂ�w��ł���B���̃v���Z�X�͂܂�����(survey)����n�܂�B���̏͂ł́A���v�w����ђ����̍l�������T�ς��A����ɂ��ƂÂ��ăf�[�^�̎��W���@��ړx�A�����Ē����ɂƂ��Ȃ��덷�ɂ��čl���Ă݂邱�Ƃɂ��悤�B
�@��������ђ������ʂւ̐ڂ����Ɋւ��ẮA���������ӂ�v����_������̂ŁA���̂��Ƃ���b���n�߂邱�Ƃɂ��悤�B
�@�܂��ŏ��ɁA�������ʂ͎��Ԃ��̂��̂�\���Ă���̂ł͂Ȃ��Ƃ������Ƃɂ͒��ӂ���K�v������B�����ɂ����ẮA�Ɋe�҂̐^�̈ӌ����\����Ă��邩�ǂ����͂킩��Ȃ����A����̎d���ɂ���Ă͂��܂��܂ȓ��v�������o�Ă��邱�ƂɂȂ�B�܂�A�������ʂ͂��̂܂܂ʼn��炩�̎��Ԃ�\�������̂ł͂Ȃ��B�������A�������ʂ́u���鎿��ɑ��āA����l���炠����Ԃ��Ă���v�Ƃ����A�܂��Ɂu�����v�̏W�c�I�Ȑςݏd�˂ł���B���v�I�ȏ������{���ꂽ�������ʂ́A�W�c�����邽�߂̈�̎w�W(index)�Ȃ̂ł���B
�@���̎w�W�����Ԃ��̂��̂Ǝ��̂͌��ł���B���̎���(���w�W)�������Ӗ����邩�́A�ΏۂƂȂ��Ă���Љ�邢�͊�Ƃ̓����Ɠ˂����킹�邱�Ƃɂ���Ă͂��߂Ă킩���Ă�����̂ł���B�Ⴆ�A���}�x�����͑I���̍ۂ̐��}�̓��[���Ƃ͈�v���Ȃ����A���}�x�����̐��ڂ͐�����̍s�������邽�߂̈�̎w�W�ƂȂ��Ă���B�����āA���}�x�����̐��ڂ𑼂̗l�X�ȗv���Ƒg�ݍ��킹�čl���邱�ƂŁA���}�̓��[����肤�d�v�Ȏ肪����ɂ��Ȃ�̂ł���B�܂�A���v�������ꂽ�������ʂ͈�̎����ł���A���̎����������Ԃ�T��肪����Ȃ̂ł���B
�@���ɁA�������邢�͓��v�ł͈��ʊW�͕�����Ȃ��Ƃ������Ƃɂ����ӂ���K�v������B����2�ϐ�x��y�Ƃ̊ԂɈ��ʊW�����݂���Ƃ������Ƃ������邽�߂ɂ́A����3�̏�������������Ă���K�v������B
�@����3�̏����������Ƃ͉\�ł��낤���B���̂����ꌩ�������2�͎��͒B���\�ł���B1�����̒����ł����Ă����╶���H�v���邱�ƂŁA�Ⴆ�A�ϐ�x�ɂ��Ă͌����_�ł̒l�A�ϐ�y�ɂ��Ă�1�����O�̒l���v���o���ĉ��Ă��炤�Ƃ����悤�ɂ���A�ϐ��ԂɎ��ԓI�������ۂ����Ƃ͂ł���B�ϐ����̂̎��ԓI�����ƁA�f�[�^���W�ɍۂ��Ă̎��ԓI�����Ƃ͕ʂ��̂Ȃ̂ł���B���́A1��3�ŁA���̈��ʕϐ��̉e������������ɂ�x��y�Ƃ̊Ԃɑ��ւ����݂��邱�Ƃ������Ȃ��Ă͂Ȃ�Ȃ�(���ւɂ��Ă���4���Ō�q)�B�������A���ݓI�ɂ́A���̂悤�ȕϐ��͖����ɑ��݂��Ă���̂ł����āA�ǂ̕ϐ������f���ɓ���邩�̑I���͗��_�I�l�@�ɂ������Ă���̂ł���B���������āA����1��3��2�����������Ƃ͖{���I�ɕs�\�ł���B2�ϐ�x��y�Ƃ̊ԂɈ��ʊW�����݂��邱�Ƃv�I�ɗ����邱�Ƃ͂ł��Ȃ��B
�@�l���Ă݂�A�����[���쐬����i�K�ŁA�ӎ����Ă���A���Ă��Ȃ��Ɋւ�炸�A���ɕϐ��̑I�����s���Ă��܂��Ă���̂ł���A�Öق̂����ɉ��炩�̈��ʊW��O��ɂ��Ă��܂��Ă��邱�ƂɂȂ�B�����f�[�^���W�ɍۂ��āA���S�I�ȕϐ��𗎂Ƃ��Ă��܂�����A���S�I�ȊT�O��Ó������������@�ő��肵�Ă��܂����肵�Ă���A���v�I�ɂ͐��������͂����ۂɂ͌�������ʂ����Ƃɂ��Ȃ�B
�@����ɁA���ւ͕������̂Ȃ��Ώ̐��̂��鐫���ł��邩��A���Ƃ����ւ�����Ƃ킩���Ă��A���͎҂����炩�̗��_�Ɋ�Â����A�������͎����̓��ōl���邩���ď�ݒ肵�Ȃ�����A�ϐ��Ԃ̈��ʂ̕��������߂邱�Ƃ͂ł��Ȃ�(�Ⴆ����5�͑�6�����Q�Ƃ̂���)�B���̈Ӗ��ł́A�ǂ�ȓ��v�I���@�����ɂ̈��ʊW���������Ƃ͂ł��Ȃ����A�����������ʊW�����݂��邱�Ƃ��������Ă͂���Ȃ��̂ł���B���ǁA�������邢�͓��v�ł͈��ʊW�͂킩��Ȃ��B
�@����ł́A�����͂ǂ��������ړI�ōs����̂ł��낤���B�܂���������̂��A���O�̒m���̐��x�����コ���邱�Ƃł���B���̑�\�́A�ʏ�̌����_���Ȃǂɂ݂���悤�ɗ��_�Ɋ�Â��������̍\�z�Ƃ��̌��ł���B���������ꂾ���ɂ͌���Ȃ��B�����P�ɒ��������A���{���A���̌��ʂƂ��ē���ꂽ���v�������g���Ƃ��������ł��A����͎���̒m���A�펯�A����x��������Ă��邱�Ƃ��Ӗ����Ă���B�Ȃ��ɂ́A���ʂ̈ӊO�������҂��Ē������s���l�����邪�A��������Ē������l���邱�Ƃ́A�����̖{����������Ă���Ƃ����Ă悢���낤�B�����͉����Ƃ܂ł͂����Ȃ��Ă��A���Ƃ��Öق̂����ɂł���������ʊW�ɂ��Ă̎��O�̒m���𗘗p���Đv�������̂ł���A���O�̒m�����s�\���ł���A�q�A�����O�����╶���Ȃǂ�ʂ��āA������x�̒m���̊l�����}����ׂ��ł���B���̂悤�ɂ��āA�����̐v���O����ɍs���Ă���A�������ʂɈӊO���������邱�Ƃ͂قƂ�ǂȂ��B
�@�������ӊO�Ȓ������ʂ�������悤�Ȃ��Ƃ�����A�������@���Ɍ�肪�Ȃ��������A���邢�͎������Ƃ�ł��Ȃ��l���Ⴂ�����Ă��Ȃ����������܂��^���Ă݂�K�v������B�o���I�ɂ́A�u�ӊO�ȁv�������ʂ́u���������ȁv�����v���琶�܂�邱�Ƃ������B�u�펯���悤�Ȓ������ʁv�͊�{�I�ɂ͂��蓾�Ȃ��ƐS���āA�������邢�͒������ʂɐڂ���ׂ��ł��낤�B�ǂ������ł́A����O�̂��Ƃ�����O�Ɍ��ʂƂȂ��ďo����̂ł���A���������邱�Ƃɂ��A����܂Ŕ��R�Ƃ���炵���X��������Ɗ����Ă������Ƃ��A��萸�m�ɓ��v�����ƂȂ��Ēm�蓾��悤�ɂȂ���̂ł���B
�@�����̂�����̖ړI�́A���̎��̒����̂��߂̃q���g�A�q�����L�邱�Ƃł���B�펯���悤�Ȓ������ʂ͊�{�I�ɂ��蓾�Ȃ��ƐS���āA�O����Ȓ����v���s�����ɂ�������炸�A�ӊO�ȁA���邢�́A����܂ŋC�Â���Ă��Ȃ������V���������E�W�����邱�Ƃ�����B�����鎖�������ł���B���̎��ɂ́A������x�������s���Ă݂Ȃ��Ă͂Ȃ�Ȃ��B�܂�A�J��Ԃ��������o�傷��Ƃ����̂��A�����̖{���̎p�ł���B�����āA���̎�����W��_���I�ɂǂ̂悤�ɐ����ł��邩����ɍl���Ă����p������ł���B
�@���ɏq�ׂ��ʂ�A���v�w�Ƃ͉Ȋw����S�̌����ł���A�Љ�Ȋw�̕���ɂ����ẮA�Љ�A�o�ρA�o�c���ۂ��܂߂āA�����̌��ۂ��ǂ�Ȃӂ��ɂȂ��Ă���̂��ׂ�w��ł���B���v�����Ŏ������L�q���邱�Ƃ�ڎw���Ă͂��邪�A�_���ݏo�����Ƃ͂ł��Ȃ��B�_���͏�ɐl�Ԃ̓��̒����琶�ݏo�������̂ł���B�����āA���̘_����펯�Ƃ��Ēm���Ă��邱�Ƃ̐��x�����コ���邱�Ƃ��A���v�����̎�ړI�Ȃ̂ł���B
�@�{���ł́A�����������v�����̎��ۂ̎p���ł��邾����̓I�����m�ɃC���[�W���Ă��炤���߂ɁA��2���ȍ~�ɓo�ꂷ�铝�v�����A���͂ɗp����f�[�^����͂��߁ASAS�v���O�����̗�Ȃǂ��A���ׂĈ�т��āu�g�D�������̂��߂̏]�ƈ��ӎ������v��f�ނƂ��āA�ˋ�ł͂Ȃ����ۂ̂��̂�p���Ă���B���̒����̏ڍׂɊւ��ẮA��6���œ��v�����̗�Ƃ��āA���̒����菇�ƕ��@���A���ۂɗp����ꂽ�ڍׂȎ����ƂƂ��Ɏ��グ����B��6���͂��Ƃ��Ɠ��v�����}�j���A�����Ӑ}���ď�����Ă���̂ŁA�����̂���ǎ҂́A��2���ɐi�ޑO�ɓǂ�ł����ƁA���v�����̊��o�����߂邾�낤�B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�́A1986�N�ȗ����N6���`���N1����8�J���������āA(��)���{���Y���{���o�c�A�J�f�~�[�u�l�Ԕ\�͂Ƒg�D�J���v�R�[�X��ɂ��āA�M�҂ɂ���ČJ��Ԃ��J��Ԃ����E���{����Ă������̂ł���B1991�N�܂łɁA�ׂ̂Ŗ�50�ЁA��5,000�l�ׂĂ����B��Q�͈ȍ~�ł́A���̂�������N�x�̒����f�[�^���f�[�^��Ƃ��Ĉ������Ƃɂ����B
�@���̒����ł́A��ƊԂł̉��f�I�Ȍ����O���[�v�����A���̃����o�[��Ƃ̊Ԃœ����ɓ���̏]�ƈ��ӎ��������s���A��ƊԁE�E��Ԃ̔�r�W�v���s���B���Ђ̎����m�b����Ȃ���A�������ʂ̊�ƊԔ�r�ɂ���āA���Ђ̕�������_��T��A���ጤ�����s���Ƃ����v���Z�X���J��Ԃ����ƂŁA�����O���[�v�𒆐S�Ƃ��đg�D�̊������Ɋւ����蔭����}��̂ł���B���́u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A�]�ƈ��̈ӎ��������s�Ȃ����Ƃ��_�@�Ƃ��Ė�蔭���v���Z�X��i�߂Ă������ƂɂȂ��Ă���B
�@�������Ė��N�J��Ԃ��J��Ԃ��s�Ȃ��邱�̒�����ʂ��������m�E�n�E�̒~�ςŁA�o�c�g�D��ΏۂƂ������v�����͐������ꂽ���̂ɂȂ����A�q�A�����O�����Ɠ��v�I�Ȕ�r�����̌J��Ԃ��T�C�N�����A�g�D�J��(organization development)�A���邢�͓��{�I�ɂ����Αg�D������(organizational activation)�ɂ����鐔�ʓI��@�Ƃ��Ă��Ȃ�̌��ʂ������Ă��邱�Ƃ��o���I�ɖ��炩�ɂȂ��Ă����B���ɒ������ʂ̓��v������O�ɂ��Ă̎���I�ȃq�A�����O�����͂��Ȃ���ʓI�ŁA�I�m�Ɋj�S�I�Ȏ����ɂ��ĕ����o�����Ƃ��\�ɂ��Ă����B����́A���ʓI�ȃq�A�����O�����̂��߂ɓ��v���������Ă���Ƃ����Ă������قǂł���B
�@���v�I�ɏ������ꂽ���ʂ́A�����Δ팱��ƂɂƂ��Ă͈ӊO�Ȑ����ł���炵�����A�O�������O�҂Ƃ��Ċώ@���Ă��錤���҂ɂƂ��ẮA�Ȃ��ӊO�Ɗ�����̂������ɋꂵ�ނ��Ƃ��قƂ�ǂł���B��O�ғI�ɂ́A���v�����͎��O�̃q�A�����O�����̓��e��f���ɔ��f�����A�o���I�A�펯�I�ɂ����Ƃ��Ȃ��̂��肾����ł���B�����āA�����A���̌���������s���鎖��I�ȃq�A�����O�����ɂ���āA1��Ƃ̓����̐l�Ԃ��������́u�ӊO���v�̍a�͂ǂ�ǂ߂��Ă������ƂɂȂ�B���̈Ӗ��ł́A1��ƂƂ��������ĕ��I�Ȑ��E�ɂ����ʗp���Ȃ��O��A�펯���A���v�����̂������������������ɂ��āA�����ɂ���Ċ��p�𔗂��邱�ƂɂȂ�̂ł���B����͂��̏͂̒��ł��ꂩ�爵����������Ɠ����_���ł���B�u�����̏펯���悻�̏펯�v�Ƃ����������A���v�f�[�^�ɂ���Ċ��p����邱�Ƃ��Ӗ����Ă���B�����������Y��Ƃ̃����o�[�����ʂ��Ă����Ă���O��A�펯�̋q�ϓI�ȓ���Ƌᖡ�E�������g�D�������ɂƂ��Ă͏d�v�Ȃ̂ł���B
�@����ł́A���������v���Z�X�ɂ����āA���v�w���ǂ̂悤�Ȗ������ʂ����Ă���̂����A�����ΏہA���f�[�^�Ƃ̊W���l���Ȃ���A���������v���Z�X�̌o�߂ɂ��������āA�����Ώۂƒ����̎�ށA���f�[�^�Ɠ��v�����̏��ԂɌ��Ă������Ƃɂ��悤�B
�@���������v���Z�X�͂܂��ϑ�(observation)����n�܂�B����͎��R�Ȋw�ł��Љ�Ȋw�ł������ŁA���R�Ȋw�̕���ł́A����͈�ʂɎ���(experiment)�Ƃ��A����Ɋւ��铝�v���_�Ƃ��Ắu�����v��@�v������B�����A�Љ�Ȋw�̕���ł́A����͒���(survey)�Ƃ��A���̓��v���_�́u�Љ���@�v�ł���B
�@�Љ�Ȋw����ł̒����ɂ����ẮA�Ⴆ�A�l�A���сA�E��A��ЂȂǂ������̒P�ʂƂȂ�B�����āA�����̑ΏۂƂȂ肤�邷�ׂĂ̒P�ʂ��W�߂����̂̂��Ƃ��W�c(population)�Ƃ�ԁB��W�c�Ƃ́A�����Ώۂ̏W�܂�ł����āA�����ɂ���āA����ɂ��ĉ��炩�̌��_���������Ƃ��Ă�����̂ł���B
�@�����̑ΏۂƂȂ�P�ʂ̂��Ƃ͗v�f(element)�Ƃ��Ă��B��������������������A��W�c�Ƃ͂܂��ɏW���ł���A����̗v�f�����̒��Ɋ܂܂��邩�ǂ����ɂ��Ă̖��m�ȋK��(���[��)���Ȃ��Ă͂Ȃ�Ȃ��B���̃��[���ɂ́A�ʏ�́A�P�ʂ��̂��́A���ԁA�ꏊ�ȂǂɊւ���L�q���܂܂�Ă���B��W�c�͒����҂���Ɨ��ɑ��݂��Ă�����̂ł͂Ȃ��āA�����҂���̓I�����m�ɐݒ肷�ׂ����̂ł���B
�@�������@�ɂ��ẮA���v�w�̒��ł͊��ɏq�ׂ��悤�Ɂu�Љ���@�v����舵���ׂ��ۑ�ł��邪�A�����ł����܂��ɐ������Ă������B����ɒ����Ƃ����Ă��A����ɂ͂��܂��܂Ȏ�ނ�����A�����Ώۂł����W�c�̑傫�����W�c�̐��ɂ���ĈقȂ�����ނ̒������s����B�܂��ŏ��ɁA��W�c�̑傫���ɂ���Ď��̓�̒������@���I�������B
�@�S�������ƕW�{�����̂ǂ����I�����ׂ����́A��W�c�̑傫���A�����ɕK�v�ȘJ�́A�R�X�g�ɂ���Č���B�Ⴆ�A�S�������̑�\��Ƃ��ẮA��������(�l��census)������B���������́A���߂�ꂽ�N��10��1�����݂̓��{�̑S�l����Ώۂɂ��čs����S�������ł����āA1920�N(�吳9�N)�Ȍ�T�N���Ƃɒ���I�ɍs���Ă���B(�������A�푈�̉e���̂��߂ɁA1945�N(���a20�N)�̒����͎��{���ꂸ�A1947�N(���a22�N)�ɗՎ����������{���ꂽ�B) ��ʂɁA���������ɑ�\�������{�S����ΏۂƂ���S�������́A���z�̔�p�Ƒ�ʂ̐l���ƒ������Ԃ�v����B���������āA���������ȊO�ɂ́A���Ə����v�����A�_�ыƃZ���T�X�A�H�Ɠ��v�A���Ɠ��v�ȂǁA�S�������̐��͌����Ă���B���ۂɁA����ꂪ�u���{�́����ɂ��Ă̒����v�Ƃ��Ă悭���ɂ���̂́A���̂قƂ�ǂ��W�{�����ł���B�W�{�����ɂ��ẮA��ł��̏͂̒��ł��ڂ�����������B
�@�����Ƃ��A���̂悤�ɒ����Ƃ����Ώ]���͂قƂ�ǕW�{�������Ӗ����Ă����̂ł��邪�A�ߔN�̒������R���s���[�^�E�e�N�m���W�[�̐i���́A��̊�Ƃ̏]�ƈ��ׂ���x�ł́A�S���������\���\�ɂ��Ă��܂����B�p�[�\�i���E�R���s���[�^�ł���A����l�K�͂̒������قƂ�ǖ��Ȃ��W�v�A���͂ł���B���Ɍo�c����ɂ����ẮA�W�{����������ɂȂ���������炸����Ă��邾�낤�B
�@���ɁA���������W�c�̐��ƒ������_�ɂ���āA�����͕\1.1�̂悤�ɁA���f�I�����A��r�����A�p�l�������A�J��Ԃ�������4��ނɕ��ނ����B���̂�����{�ɂȂ�̂́A��̕�W�c�ɑ���1�����̒����ł��鉡�f�I�����ł���B���̒������@�́A���̉��f�I������F�X�Ƒg�ݍ��킹�����̂ł���B
�\1.1�@�������@�̎��
| �������_ | ��W�c | |
|---|---|---|
| �����W�c | ������W�c | |
| �ꎞ�_ | ���f�I���� | ��r���� |
| �������_ | �p�l������ | �J��Ԃ����� |
�@�������_���قȂ�A��W�c���K�肷�鑼�̃��[���������ł��A�����ɂ͕�W�c�̗v�f�͈قȂ�̂ŁA���̂悤�ȏꍇ���A�����ɂ͌J��Ԃ������ɂȂ�B��������ʂɁA�������_���قȂ邾���ŁA��W�c���K�肷�鑼�̃��[���������Ȃ�A���̂悤�Ȓ������瓾��ꂽ�f�[�^�́A���n��f�[�^(time-series data)�Ƃ���B���n��f�[�^�ɂ���āA���Ԃ̌o�߂ɂ��ω���َ��_�Ԃ̊W��m�邱�Ƃ��ł���B�p�l���������A�p�l�����Œ肷��ԁA��W�c�̗v�f�͕ϓ����Ȃ��Ɖ��肵�āA���n��f�[�^�邽�߂ɍs������̂ł���B
�@������ɂ���A�������ʂ╪�͌��ʂ𐳂����������邽�߂ɂ́A���̒������ǂ̂悤�ɂ��čs�Ȃ�ꂽ�ǂ�Ȏ�ނ̒����ł��邩��m��Ȃ��Ă͂Ȃ�Ȃ��B��������ƁA�������ʂ̓��v������������l�����������ł��邪�A���v�����͒������@�Ə�Ƀy�A�ŕ]�������ׂ����̂Ȃ̂ł���B(�����K���1.1)
�@�����̌��ʂ́A���f�[�^�A�������͒P�Ƀf�[�^�Ƃ��A���v�I�L�q�̑f�ނƂȂ�B�f�[�^�Ƃ́A�W�{�����Ȃ�ΕW�{�A�S�������Ȃ�Ε�W�c�ɑ�����e�v�f�Ɋւ���ϑ��l�̂܂Ƃ܂���w���Ă���B�ŋ߂̂悤�ɁA�R���s���[�^���g�����W�v�A���v���͂����S�ɂȂ��Ă���ƁA�f�[�^�̏�����̕X���l����A�ϑ��l�̓J�i��A���t�@�x�b�g�Ȃǂ̕����ł͂Ȃ��āA���l�ŕ\����Ă��邱�Ƃ��]�܂����B
�@�Ƃ���ŁA�ϑ��l�����l�ƂȂ��Ă���A�`���I�ɂ͂����̊Ԃ̉��Z���\�ɂȂ�B�������A���ӂ��K�v�Ȃ̂́A�ϑ��l���ǂ�Ȏړx(scale)�ɂ���đ��肳�ꂽ�̂��ɂ���āA�ǂ̂悤�Ȑ����̉��Z���s�����Ƃ��ł��邩�����܂��Ă���Ƃ������Ƃł���B����̓R���s���[�^�ɔ��f�ł��邱�Ƃł͂Ȃ��āA�l�Ԃ̑��ł�����ƃR���s���[�^�Ɏw�����Ă����ׂ����Ƃł���B�悭�p������ړx�̕��ނƂ��ẮA����4������B
�@���`�ړx�A�����ړx�ɂ��ƂÂ��f�[�^�̂��Ƃ����I(�萫�I)�f�[�^(qualitative data)�Ƃ����A�Ԋu�ړx�A�䗦�ړx�ɂ��ƂÂ��f�[�^�̂��Ƃ�ʓI(��ʓI)�f�[�^(quantitative data)�Ƃ����B��̃��X�g��1����4�ւƂȂ�ɂ��������āA�ړx�Ƃ��Ă͏�ʂɂȂ��Ă����B�܂�A��ʂ̎ړx�ɂ��ƂÂ��ϑ��l�ɂ́A���ʂ̎ړx�ɂ��ƂÂ��ϑ��l�̈Ӗ��A����т���ɉ\�ȉ��Z����܂���Ă���B�ϑ��l�̉��Z�\���́A
�����������Z�\���ɂ��Ă͏\���ɒ��ӂ�˂Ȃ�Ȃ��B
�@�����ɂ���ē���ꂽ���f�[�^�ɑ��ē��v�������{�������̂����v�����ł���B����́A�悭�������ʂƂ�����B���̂Ƃ��A�^����ꂽ���f�[�^�ׁA���̋K�������瓝�v�I�@��������L�q���v�w(descriptive statistics)�����邱�ƂɂȂ�B�܂�A�}�\�ɂ���ăf�[�^�����A���ρA���U�Ȃǂ̓����l�ɂ���ăf�[�^��v��Ƃ����悤�ɁA�f�[�^���E�v�āA��W�c��W�{�̏W�c�Ƃ��Ă̓������L�q����̂ł���B�������A�f�[�^�𐔒l�I�ɗv��ꍇ�ɂ́A(2)�ŏq�ׂ��悤�ɁA�f�[�^�����肳�ꂽ�ړx�����ɂȂ�B�f�[�^�̉��Z�\���ɂ��ẮA�f�[�^�������n�߂�O�ɁA�K���l���Ă����K�v������B
�@�Ƃ���ŁA���v�w�̖����̓f�[�^�̐����E�v���ł͂Ȃ��B�S�������̂悤�ɁA��W�c���\�����邷�ׂĂ̗v�f�ׂ钲���̏ꍇ�ɂ́A�L�q���v�w�����ŏ\���ł���A����ɂ���ē����錋�ʂɁA����ȏ�Ȃɂ��t��������ׂ����Ƃ͂Ȃ��B�Ƃ��낪�A���p�ɂɍs����W�{�����̂悤�ɁA��W�c����K���ȕW�{�𒊏o���āA���̕W�{�ɂ��ē���ꂽ�m���ɂ��ƂÂ��āA��W�c�ɂ��Ă̐��_���s���ꍇ�A�Ȃ��S���ׂ��ɂ��̈ꕔ�̕W�{�����邾���ŁA��W�c�S�̂ɂ��Ă̐��_���\�ɂȂ�̂��Ƃ����^�₪�킢�Ă���B�����Ő������v�w���d�v�Ȗ������ʂ������ƂɂȂ�B
�@���́A��W�c�̕����ł���W�{���A����ג��o�ɂ���đI��Ă���A�m���Ƃ����_�����u��ʂ��āA��������S�̂�m�邱�Ƃ͉\�Ȃ̂ł���B���̂Ƃ��A��W�c�S�̂ł͂Ȃ��āA���̈ꕔ���ώ@���āA���̌��ʂɂ��ƂÂ��āA�S�̖̂@�����̔������邱�Ƃv�I����(statistical inference)�Ƃ�ԁB���v�I�����ɂ́A��������(hypothesis testing)�Ɛ���(estimation)�Ƃ�����̒�������B�������A�W�{�������瓱���o���ꂽ���_�́A��������W�{�𒊏o������W�c�ɂ��Ă̂ݑÓ����邱�ƂɂȂ�B�����āA�m���_����ѓ��v�w���_�ɂ���āA�W�{���o�ɂƂ��Ȃ��덷���q�ϓI�ɕ]�����邱�Ƃ��\�ɂȂ�̂ł���B
�@���̂悤�ɁA�����ɂ����ẮA�����ɂƂ��Ȃ��Ĕ�������덷��}���A���邢�͂��̑傫����]�����邱�Ƃ��d�v�ɂȂ�B���́A�����ɂƂ��Ȃ��덷�͕W�{���o�ɂƂ��Ȃ����̂���ł͂Ȃ��A���Ƃ��W�{���o���s�킸�ɁA�S���������s�����ꍇ�ł�����������덷�����݂���B�����ŁA���߂ł́A�������������ɂƂ��Ȃ��덷�ɂ��Ă܂Ƃ߂Ă������B
�}1.1�@�Љ�Ȋw�ɂ����铝�v�w�̖���
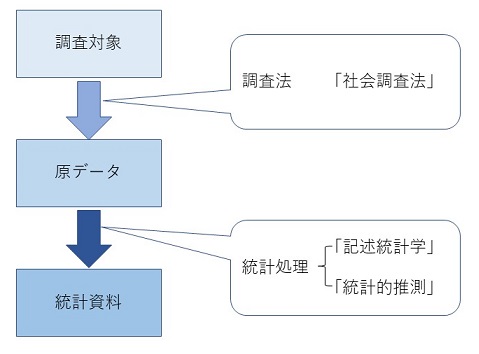
�@�����ɂƂ��Ȃ��덷�ɂ́A�}1.2�Ɏ����悤�ɕW�{�덷�Ɣ�W�{�덷��2��ނ�����B���̂����A��W�{�덷(non-sampling error)�́A�S�������ł��W�{�����ł������钲���ߒ��ł̌덷�ł���A����ɂ��ċq�ϓI�ɕ]�����邱�Ƃ͓���B���v�w���_�ł͕W�{�덷�ɂ��ẮA���Ȃ�ڍׂȋᖡ���s���邪�A��W�{�덷�ɂ��ẮA�Ȃ�����̊�������B�������A�����ɍs�Ȃ���ʏ�̒����ł́A��W�{�덷�̑��݂Ƃ��̑傫���́A���Ȃ�[���Ȗ��ƂȂ��Ă���B
�}1.2�@�����ɂƂ��Ȃ��덷
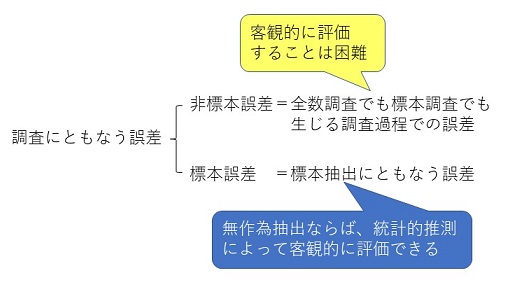
�@��W�{�덷�Ƃ��Ă�
�@��W�{�덷�̂����A1. ���̌덷�A2. �̕�ɂ��ẮA�ǂ̂悤�Ȓ������@���Ƃ�̂��ɂ���āA���̂����悻�̑傫���������Ă���B���⒲���[���g�����������@�Ƃ��ẮA�傫�������āA�\1.2�̂悤�ȕ��@���l������B
�\1.2�@�������@�̕���
| �L���� | ���u | �z�z | ��� | |
|---|---|---|---|---|
| �ʐڒ����@(interview survey) | ���L�� | �~ | ������ | ������ |
| �ʑO�L���@ | ���L�� | �~ | ������ | ������ |
| �z�z����@(���u(�ҵ�)�@) | ���L�� | �� | ������ | ������ |
| �X������@ | ���L�� | �� | �X�� | ������ |
| �X���@(mail survey) | ���L�� | �� | �X�� | �X�� |
�@�\1.2�̒��ɂ��鑼�L��(�܂��͑��v���Ƃ�����)�Ƃ́A�������������[�ɂ��������Ď��₵�A����ɑ��钲���Ώۂ̉����������[�ɋL����������ł���B����ɑ��āA���L��(�܂��͎��v���Ƃ�����)�Ƃ́A�����Ώۂ������Œ����[�̎����ǂ݂Ȃ���A�����ʼn��[�ɋL����������ł���B
�@�����̒������@�̔�r�͕\1.3�̂悤�ɂȂ�B��W�{�덷�Ƃ̊W�ł́A������A�̕�ɒ��ӂ��Ȃ���A�������@��I������K�v������B
�\1.3�@�������@�̔�r
| �ʐڒ����@ | �ʑO�L���@ | �z�z����@ | �X������@ | �X���@ | |
|---|---|---|---|---|---|
| ������p |
|
|
| ||
| �����[�̔z�z����ɗv���鎞�� |
|
|
| ||
| �����[�̉���� |
|
|
| ||
| �����Ώۖ{�l�̊m�F |
|
| |||
| ����̈Ӗ��̗���x |
|
| |||
| �̕� |
|
| |||
�@�ʏ�A�X���@�̉�����͂���߂ĒႭ�A�\3�̒��̐�����������ɒႭ�A10%���������̂��Ƃ������B�X���@�ʼn�����������Ƃ��ɂ́A�ނ���A�W�{���o�̎d���⒲���̎d�����^���Ă݂������悢�Ƃ�����قǂł���B������ɂ���A��ʂɂ́A�X���@�Ŏ��W���ꂽ�f�[�^�͒������̂��߁A���ꂩ��(3)�ŏq�ׂ閳�ɂƂ��Ȃ���W�{�덷���傫�����A���v�I�����͂��ĂɂȂ�Ȃ��̂ŗv���ӂł���B
�@���̕\3�̒��ŁA�ʐڒ����@�A�ʑO�L���@�Ɍ�����̕�́A��ɉ҂̓��������̍ۂɕۂ���Ă��Ȃ����Ƃɂ����̂ł���B���Ȃ��Ƃ��̍ۂɂ́A�҂͒�������ڂ̑O�ɂ��Ă���A�������̑��ł��N�����Ă���̂���F�����Ă��邩��ł���B���������āA�Ⴆ�Ή̕��1�ɂ��ẮA����������w�ł��邩�A�j�q�w���ł��邩�A���q�w���ł��邩�ɂ���āA���h��p������������̌X�����قȂ��Ă��邱�Ƃ��\���ɍl������B
�@�܂������������ɂ��Ȃ��Ă��A�������̈ӌ��ɂ���Ă��e�����邩���m��Ȃ��B�u���������̔�r�����v(���R 1984, p.66)�ɂ��ƁA�u��Ղ�M���邩�H�v�Ƃ�������ɑ��āA�\1.4�̂悤�ɒ������̈ӌ��̉e����������Ƃ�����B
�\1.4�@�������̈ӌ��Ɖ�
| �������̈ӌ� | �� | ||
|---|---|---|---|
| ��Ղ�M���� | ��Ղ�M���Ȃ� | �v | |
| ��Ղ�M���� | 25% | 75% | �@119 (100%)�@ |
| ��Ղ�M���Ȃ� | 12% | 88% | �@255 (100%)�@ |
�@�{���Ŏ��グ�Ă���u�g�D�������̂��߂̏]�ƈ��ӎ������v�̏ꍇ�ɂ́A�z�z����@�ɂ���āA1�T�Ԉȓ��̒Z���ԂɁA�ł��邾������(90���O��)�̉������500�l�ȏ�����邱�Ƃ�ڕW�Ƃ��čs����B���������z�z����@���\�Ȃ̂́A��Ƒ��̃j�[�Y�ɂ�����x���v�������e�ɂ��邱�ƂŁA�z�z����ɍۂ��Ă̋��͂�������Ƃ����l���I�ȑ��ʂ����ł͂Ȃ��A����������鑤�̏]�ƈ��̍�������͂Ƃ������ʂ��������Ȃ�(�\1.3�́u�̕�v�̗����Q�Ƃ̂���)�B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A��r�I�傫�Ȋ�Ƃő呲���S�̃z���C�g�J���[���ΏۂƂ��Ă��邱�ƂŁA����̈Ӗ��̗���x��������x�ۏ���Ă���̂ł���B
�@�����ŁA��W�{�덷�̂����傫�ȕ������߂�u1. ���̌덷�v�ɂ��āA���̑傫�����ǂ̒��x�̂��̂ɂȂ�̂����l���Ă݂悤�B���̌덷�́A����������������Ⴂ���ƂɂƂ��Ȃ����̌덷�E����w���Ă���B�ʏ�A�}1.3�Ɏ������悤�ɁA�����ł́A��W�c�̃��X�g�̕s���A�ҕs�݂̂��߂̒E���A���ۂȂǂɂ�钲������������āA�����[���z�z�����B���̔z�z���ꂽ�����[�̒��̖��������ł������ł����B���̂����A���S�Ȗ��́A�z�z���ꂽ�����[�̂�������s�\���������́A����͂������������������̂Ƃɕ�������B���������z�z���ꂽ���̂̊��S���ł����������[���������c��̕����A�܂������ꂩ�ꕔ�܂��͑S������Ă��钲���[���́A�S�z�z���ɐ�߂銄����������ƌĂԁB
�}1.3�@��������Ɖ����
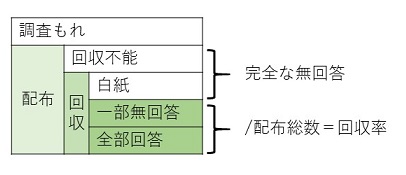
�@��ʂɁA���̌덷���d��ɂȂ�̂�
�@�����������̌덷���ǂ̒��x�̑傫���ɂȂ���̂Ȃ̂��A���ܗ�Ƃ��āAYes-No�`���̎�����l���Ă݂悤�B�������ʂ�(���Ȃ킿�ҌQ��) 60%��Yes�������Ƃ��A���ꂾ������Ɖߔ�����Yes�Ɠ������ƌ��������ł���B�������A�{���ɂ������낤���B���̒��x��Yes�䗦�ł́A���͖��ҌQ�ł�Yes��40%�ŁAYes�䗦��No�䗦�Ƃ��t�]���Ă����c�c�Ƃ����悤�ȃP�[�X���悭����̂ł���B����̃e�[�}�̒����ɑ��ẮA���̃e�[�}�ɍm��I�Ȑl�͉ɋ��͓I�����A�ے�I�ȁA���邢�͌������������Ă���l�́A���߂�ǂ���������A���ۂ����肷��Ƃ����X��������̂ŁA�ނ��낱�̒��x�̗��Q��Yes�䗦�̍��͂������ʂɑ��݂���ƍl���Ă����������悢�B
�@���ɗL������50%�Ƃ���ƁA�S�����Ώۂ�Yes�䗦�́A���҂̂��傤�ǒ��Ԃ�50%���������ƂɂȂ�B�܂�A
�@�@�@0.6�~0.5�{0.4�~0.5��0.5
�ƂȂ�B�������L������20%�Ȃ�A
�@�@�@0.6�~0.2�{0.4�~0.8��0.44
�ƂȂ��Ă��܂��A�Ȃ�Ǝ��ۂ̑S�����Ώۂł�Yes�䗦�͉ߔ���������A44%�������Ȃ��������ƂɂȂ�̂ł���B�ҌQ�����������Ƃ��̌�������Yes�䗦�Ƃ͌��_���t�]����B���͉ߔ�����No�������̂ł���B
�@����ł́A���������l��������������ʉ����āA���̂悤��Yes-No�`���̎���̖��̌덷���ǂ̒��x�̑傫���ɂȂ�̂����l���Ă݂邱�Ƃɂ��悤�B
�S�����Ώۂ�Yes�䗦
�@�@��(�ҌQ��Yes�Ґ��{���ҌQ��Yes�Ґ�)/�z�z����
�@�@��(�Ґ��~�ҌQ��Yes�Ґ�)/(�z�z�����~�Ґ�)�{(���Ґ��~���ҌQ��Yes�Ґ�)/(�z�z�����~���Ґ�)
�@�@���L�����~�ҌQ��Yes�䗦�{(1-�L����)�~���ҌQ��Yes�䗦
�@�@���ҌQ��Yes�䗦�{(1-�L����)�~(���ҌQ��Yes�䗦�|�ҌQ��Yes�䗦)�@�@�@ (1.1)
�����ŁA(1.1)���̉����������u���̌덷�v�Ƃ������ƂɂȂ�B���̖��̌덷�����ۂɌv�Z���Ă݂�ƁA�\1.5�̂悤�ɂȂ�B
�\1.5�@���̌덷(�Ԋ|�������͖��̌덷��5%�ȉ�)
| �L�� �� ��(%) | �b���ҌQ��Yes�䗦(%)�|�ҌQ��Yes�䗦(%)�b | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 90 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 80 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 70 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 60 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 50 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 40 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 30 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 20 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 10 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 0 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
�@�����ł����قǂ̂悤�ɁA���Ƃ��A�ҌQ�ł�Yes��60%�ʼnߔ�����Yes�ƌ����Ă��Ă��A���́A���ҌQ�ł�Yes��40%�������ꍇ���l���Ă݂悤�B���̂Ƃ��A���Q��Yes�䗦�̍���20%�ɂȂ�A�\1.5�̖��̗������Ƃ킩��悤�ɁA�L������50%�����̂Ƃ��ɂ́A���̌덷��10%����̂ŁA�S�����Ώ�(�W�{)��Yes�͎��͏����h�������Ƃ����t�]���ۂ��N�����Ă��܂��B
�@��ŁA��7���ŏq�ׂ�悤�ɁA�W�{���o�ɂƂ��Ȃ��W�{�덷�̖ڕW���x��5%���x�ɗ}�������ƍl���Ă���Ƃ��ɂ́A��W�{�덷�����߂ē����x��5%���炢�ɂ͗}���Ă����Ȃ��ƈӖ����Ȃ��B�����Ă��̂Ƃ��ɂ́A�����[�̉����(���L����)��80%�ȏ��ڕW�ɂ���K�v�����邱�ƂɂȂ�B����ɕ\1.5����A�����[�̗L������90%�ȏ゠��A�܂��t�]���ۂ̐S�z�͂Ȃ����Ƃ��킩��B
�@��W�{�덷�ɑ��āA�W�{�덷(sampling error)�͕W�{���o�ɔ����덷�ł���A�W�{�̒��o���@(sampling method)�ɂ���ẮA�q�ϓI�Ɏ�舵�����Ƃ��ł���B��̓I�ɂ́A���ɏq�ׂ�悤�ȗL�ӑI�o�@��p�����ꍇ�͍���ł��邪�A����ג��o�@��p���ĕW�{���o���s�����ꍇ�ɂ́A�m���_����ѓ��v�w���_�ɂ���ċq�ϓI�ɕ]�����邱�Ƃ��ł���B���ꂪ���v�I�����̗��_�ł���B�܂�A���v�I�����́A�ǂ̂悤�ȕW�{�ɑ��Ă��g����킯�ł͂Ȃ��B���̂��Ƃ����������ڂ������Ă݂悤�B
(a)�L�ӑI�o�@(purposive selection)
�@����́A�����҂��K���ɕW�{��I�ԕ��@�ł���B��Ƃ���������̊�Ƃ�����悤�ȕ��@(�@���@)��A���j�^�[���W���Ă��̈ӌ����悤�ȕ��@(����@)���L�ӑI�o�@�Ɋ܂܂��B�������A�����Ƃ��̌n�I�ȕ��@�́A���蓖�Ė@(quota method)�ƌĂ����̂ł����āA
(b)����ג��o�@(random sampling)
�@����́A�N�W�����̌����ŕW�{�ƂȂ�v�f�������_����(����ׂ�)�I�яo�����@�ł���B�����ɂ́A��W�c�̗v�f���X�g�ŁA�e�v�f�ɒʂ��ԍ������A���̒ʂ��ԍ����A�����\���������Ē��o���Ă����B���邢�́A���������0����9�܂ł̐�����2�ʂ����܂�Ă��鐳20�ʑ̂́u���������v��U���āA�o���ڂ����Ƃɂ��Ē��o���Ă����B������ȕ։��������̂ɁA�n�����o�@���邢�͓��Ԋu���o�@�ƌĂ����@������B�����ȈӖ��ł͖���ג��o�@�ł͂Ȃ����A��W�c�̑傫��n��W�{�̑傫��r�Ŋ�����n/r�ȉ��̍ő�̐���I�𒊏o�Ԋu�Ƃ��āA����I�ȉ��̖���ׂɑI���o�X�^�[�g�ԍ�����A���Ƃ͓��ԊuI�Ŕԍ����Ȃ��Ȃ�܂őI�ԕ��@�ł���B������ɂ���A����ׂɊm���I�ɒ��o������@��p����ƁA��W�c���\������S�v�f�ɂ��āA���ꂼ�ꂪ�W�{�Ƃ��Ē��o�����m�������ɂȂ�̂ŁA�W�{�̐��������W�c�̐������q�ϓI�ɕ]�����邱�Ƃ��ł���悤�ɂȂ�B���݂̓��v�w�̐���A����̗��_�͂��̖���ג��o�@��O��Ƃ��Ă���B
�@���������āA�����ł́A�L�ӑI�o�@�́u�Ȋw�I�ȁv�����ł͖{�����̑O�̗\���I�����ŗ��p������x�ɂ��ׂ��ł���Ƃ���Ă���B������
�@�������A�L�ӑI�o�@���̗p�����ꍇ�A���邢�͗L�ӑI�o�@�ɂ���ē���ꂽ�f�[�^������ꍇ�ɂ́A�\1.6�ɂ܂Ƃ߂�ꂽ�����ɒ��ӂ��Ȃ��Ă͂Ȃ�Ȃ��B���Ȃ킿�A�L�ӑI�o�@�ł́A����ג��o�@�Ƃ͈قȂ�A�f�[�^�͕�������A���������x�͍����Ă����Ăɂ͂Ȃ�Ȃ��Ƃ������Ƃ�F������K�v������B�����āA�L�ӑI�o�@�œ���ꂽ�f�[�^�ɂ��ẮA���v�I�����͖��͂��Ƃ������Ƃł���B���Ȃ킿�A����ג��o�@�ɂ���Ē��o���ꂽ�W�{�ɂ̂݁A���v�I�������\�Ȃ̂ł���B����ɑ��āA����ג��o�@�ł́A���������邱�Ƃ��ł��邵�A���x�͕W�{�̑傫����傫�����邱�Ƃō��߂���B�������A���x�̕]�����q�ϓI�ɍs�����Ƃ��ł���̂ł���B
�\1.6�@�W�{�����W�c�̓����𐄘_����ꍇ�̗L�ӑI�o�@�Ɩ���ג��o�@�̔�r
| �L�ӑI�o�@ | ����ג��o�@ | |
|---|---|---|
| �� | ����ł��Ȃ� | ����ł��� |
| ���x | �ӎ��I�ɗ��̂�������v�f��I��ŕW�{�ɂ��邱�Ƃō��߂��� | �W�{��傫�����邱�Ƃō��߂��� |
| ���x�̕]�� | ���� | �m���_�E���v�w�ʼn\ |
�@����ł́A����ג��o�̏ꍇ�ɂ́A�ǂ̂悤�ɂ��Ă��̂悤�Ȉ�A�̓��v�I�������\�Ȃ̂ł��낤���B���̂��Ƃ����ꂩ���5�߁`��7�߂ɂ����āA�m���A��������A����̏��Ɍ��Ă������Ƃɂ��悤�B�������A����ג��o�@�́A�W�{�덷�ɑ��ẮA���ɗL���Ȓ��o���@�ł��邪�A��W�{�덷�ɑ��ẮA�Ȃ��ۏ�����̂ł͂Ȃ��B���̂��Ƃ͏\���ɔF�����Ă����K�v������B
�@����ȍ~�A�m���̘b�����X�������A����͓�̖ړI�̂��߂ɕK�v�Ȃ��̂ł���B��́A�ʏ�A���v�������s�����ۂɂ悭�p������u�L�Ӑ����v�܂��́u�L�ӊm���v�̊T�O�𐳂����������Ă��炤���߂ł���B������́A�W�{�̑傫���̂��Ӗ��𗝉����Ă��炤���߂ł���B����́A��������悷��ۂɁA�K�ɕW�{�̑傫�������߂邽�߂ɏd�v�ɂȂ��Ă��邾���ł͂Ȃ��A���ɍs���Ă��܂��������̕W�{�덷��]������ۂɂ���{�I�ȏ��ƂȂ邩��ł���B�������A�S��������O��ɂ���ꍇ�ɂ́A����ȍ~�̐߂͕K�v���Ȃ��Ȃ�B
�@���܁A�傫��n�̕�W�c����W�{�Ƃ���r�̗v�f������o(sampling without replacement)�Ŗ���ׂɒ��o���邱�Ƃ��l���悤�B�܂�Ar�̂��̂����o���Ƃ��ɁA1���Ƃɂ����������ɖ߂����ɁA������r�����o�����Ƃ��l����B���̕W�{���o�ɂ���ē����錋��(outcome)�A���Ȃ킿�W�{�̂��Ƃł��邪�A����͕W�{�_�ƌĂ��B������\�ȕW�{�_�̏W���͕W�{���(sample space)�ƌĂ�āA���ŕ\���B
�@��) ���ܕ�W�c�Ƃ��āA�u���p���v�w�v�𗚏C����w���̏W�����l���Ă݂悤�B�w���͗��C�ԍ��ŕ\�������̂Ƃ���B�u���p���v�w�v�𗚏C����w����6�l������(n��6)�Ƃ���ƁA��W�c�͏W���o1,2,3,4,5,6�p�ŕ\�����Ƃ��ł���B���̕�W�c����A�}1.4�̂悤�ɁA�W�{�Ƃ���3�l�̊w���𒊏o����ꍇ���l���Ă݂悤(r��3)�B���̏ꍇ�A�W�{�͕�W�c���璊�o���ꂽ3�l�̊w���̑g�A���Ƃ���(1,2,3), (2,3,6)�̂悤�ɕ\�����B
�}1.4�@�傫��6�̕�W�c����傫��3�̕W�{�̒��o
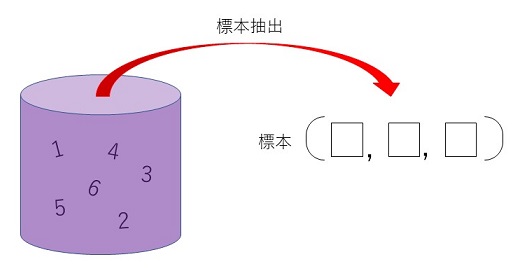
�@���̂Ƃ��A�W�{�_�������o���ƁA�W�{��ԃ��́A���̂悤��20�̕W�{�_����Ȃ�W���ɂȂ�B
| ����{(1,2,3), (1,2,4), (1,2,5), (1,2,6), |
| (1,3,4), (1,3,5), (1,3,6), |
| (1,4,5), (1,4,6), |
| (1,5,6), |
| (2,3,4), (2,3,5), (2,3,6), |
| (2,4,5), (2,4,6), |
| (2,5,6), |
| (3,4,5), (3,4,6), |
| (3,5,6), |
| (4,5,6)} |
�@���������āA�W�{�ƂȂ�w���̑g�����Ƃ��ẮA20�ʂ肪�l������B�܂�傫��6�̕�W�c����傫��3�̕W�{�𒊏o����Ƃ��̕W�{�_�̌���20�Ƃ����킯�ł���B���̏ꍇ�A�W�{��ԃ��̗v�f�����ׂĂ������������o���Ȃ��Ă��A�W�{�_�̌��́A��W�c��6�̗v�f����W�{�Ƃ���3�̗v�f���Ƃ��Ă���g�����̐��Ȃ̂ŁA���̂悤�ɂ��v�Z�ł���B
�@�@�@6C3��(6�5�4)/(3�2�1)��20
���̌v�Z���@�ɂ��ĊT�����Ă������B�܂��ŏ��ɁA��ʂɁA����(permutation)�Ƃ�n�̂��̂���r�Ƃ���1��ɕ��ׂ����̂̂��Ƃł���An�̂��̂���r�Ƃ鏇��̐��́A���̂悤�ɗ^������
�@�@�@nPr��n(n�|1)(n�|2)���(n�|(r�|1))��n!/(n�|r)!
�����ŁAn!��n(n�|1)(n�|2)���3�2�1 �ł���A�����n�̊K��(factorial)�Ƃ�ԁB0!��1 �Ƃ������Ƃ����Ă������B�܂�A��̐擪�ɉ�������̂���n�ʂ�l�����A�擪��1�����߂�A���̐擪����2�Ԗڂɂ́A�擪�ɒ�߂�ꂽ2���������c���n�|1�̒�����ǂꂩ����I��邱�ƂɂȂ�̂�n�|1�ʂ�c�c�����ė�̍Ō��1�͎c���Ă���n�|(r�|1)�̒�����I���̂ŁAn�|(r�|1)�ʂ�A���������ׂĊ|�����킹��Ƃ��̂悤�Ȏ��ɂȂ�̂ł���B
�@����ɁA�g�������l���邱�Ƃ��ł���B���܁A�Ƃ��Ă���r���ǂ̂悤�ȏ����ɕ���ł��Ă��A�g�����Ƃ��Ă͓������̂ƍl������̂ŁArPr��r!�̏���͈�̑g�����Ƃ��Đ�������ׂ����̂Ƃ������ƂɂȂ�B���������āAn�̂��̂���r�Ƃ�g����(combination)�̐���
�@�@�@nCr��nPr/r!��n!/{r!(n�|r)!}
�ƂȂ�B
�@����(event)�Ƃ́A�W�{��ԃ��̕����W���̂��Ƃł���A�Ȃ�炩�̈Ӗ��ŊS��������錋�ʂ̏W���ł���B�����قǂ�6�l�̊w������Ȃ��W�c����3�l�̊w���𒊏o�����ł́A���Ƃ��A���̂悤�Ȏ��ۂ��l���邱�Ƃ��ł���B
�@�@�@A��{(1,2,6), (1,3,5), (2,3,4)}
�@�@�@B��{(1,3,5)}
����A�͊w���̗��C�ԍ��̘a�����傤��9�ɂȂ鎖�ۂ�\���Ă���A����B�͊�̗��C�ԍ��̊w���݂̂ł���Ƃ������ۂ�\���Ă���B
�@�W�{���o(����ʓI�ɂ́u���s�v)���s���ƁA�K���W�{��ԃ��̒��̂�����̕W�{�_�ւ��������邱�ƂɂȂ�B���̎��������W�{�_�ւ�����A�ɑ�����Ƃ��A���̎���A�����N�����Ƃ����B�Ⴆ�A6�l�̊w������3�l��W�{���o����ƁA�w��1�A�w��3�A�w��5�����o�����ƁA3�l�̗��C�ԍ��̘a��9�ɂȂ�A����A�����N�������ƂɂȂ�B���͎���B�������ɐ��N���Ă���B
�@���ܕW�{������ג��o�����ꍇ���l���悤�B�Ⴆ�A���������U���āA�o���ڂ̗��C�ԍ��̊w����W�{�Ƃ��Ē��o����̂ł���B���̂Ƃ��A�W�{���o�̌��ʂ͒��o�ߒ��̋��R���ɉe������邱�ƂɂȂ�B���v�I�ōl������B��̋��R�I�����́A�W�{�̕�W�c����̃����_���Ȓ��o�����ł���B���̂Ƃ��u����A�̐��N���邱�Ƃ̊m���炵���v�܂�A�m�����͂��߂čl���邱�Ƃ��ł���B��ʂɁA���N����m�����l�����鎖�ۂ��m������(probability event)�Ƃ����BPr(A)�ŁA����A�̐��N����m����\�����Ƃɂ��悤�B
�@����ł́A�W�{������ג��o�����ꍇ�ɁA�ǂ̂悤�Ɋm��Pr(A)��t�^���邱�Ƃ��ł���̂ł��낤���B����n�̕W�{�_����Ȃ�W�{��ԃ����l����B����ג��o�ɂ���ĕW�{�𒊏o�������An�̕W�{�_�̂ǂ�����A���N���邱�ƂɊւ��Ắu�����x�Ɋm���炵��(equally likely)�v�B���������āA���̂Ƃ��A����A�̐��N����m��Pr(A)�́A����A�ɑ�����W�{�_�̌�k��m(A)�ŕ\���ƁA
�@�@�@Pr(A)��m(A)/m(��)��k/n
�ƒ�`�ł���B�����قǂ̗�ł́A
�@�@�@m(��)��20
�@�@�@m(A)��m({(1,2,6), (1,3,5), (2,3,4)})��3
�@�@�@m(B)��m({(1,3,5)})��1
�Ȃ̂ŁAPr(A)��3/20�APr(B)��1/20 �ƂȂ�B�������āA���̖���ג��o�̂Ƃ��ɒ�`�����m���́A�W�{�_�̌��A�܂�A�N������̏ꍇ�̐��̐����グ�ɋA����킯�ł���B
�@�m���ϐ�(random variable)�Ƃ͕W�{��ԃ��̏�Œ�`���ꂽ�����l���Ƃ��X(��)�C�ց��� �̂��Ƃł���B�W�{���o�̌��ʂƂ��ĕW�{�_�ւ���܂�ƁA�����lx��X(��)����܂�B�t�ɁA{��: X(��)��x}�ƏW�����`����ƁA����͕W�{��Ԃ̕����W���ƂȂ�B�������͊m�����ۂƂȂ�̂ŁA�m�� Pr({��: X(��)��x}) ��^���邱�Ƃ��ł���B��ʂɁA���� Pr({��: X(��)��x}) ���ւ��ȗ����āAPr(X��x)�Ə����B�܂�A�m���ϐ��́A���ꂪ�Ƃ�e�l�ɑ��āA���ꂼ��m�����^�����Ă���ϐ��Ȃ̂ł���B���Ȃ݂ɁA�m���ϐ���X�̂悤�Ƀ��[�}���̑啶���ŕ\���B
�@��̑���) �����قǂ̗�Ɠ��l�ɁA�u���p���v�w�v�𗚏C����w���̏W���o1,2,3,4,5,6�p���W�c�Ƃ���B���̂����A���C�ԍ�1,2,3�̊w���́u��b���v�w�v�̎����ɍ��i���A�P�ʂ��擾���Ă��邪�A����3�l�̊w���́u��b���v�w�v�̒P�ʂ��擾���Ă��Ȃ��B�����ł��܁A3�l�̊w����W�{�Ƃ��Ē��o���邱�Ƃ��l���A�m���ϐ�X�ł��̕W�{���́u��b���v�w�v�̒P�ʎ擾�Ґ���\�����̂Ƃ���B�W�{�̑傫����3������A�m���ϐ�X(��)��0,1,2,3�̂����ꂩ�̒l���Ƃ邱�ƂɂȂ�B
�@�@�@{��: X(��)��3}��{(1,2,3)}
�@�@�@{��: X(��)��2}��{(1,2,4), (1,2,5), (1,2,6), (1,3,4), (1,3,5), (1,3,6), (2,3,4), (2,3,5), (2,3,6)}
�@�@�@{��: X(��)��1}��{(1,4,5), (1,4,6), (1,5,6), (2,4,5), (2,4,6), (2,5,6), (3,4,5), (3,4,6), (3,5,6)}
�@�@�@{��: X(��)��0}��{(4,5,6)}
����ג��o�ɂ���ĕW�{�𒊏o�������A20�̕W�{�_�̂ǂꂪ���N����̂������x�Ɋm���炵���̂�
�@�@�@Pr(X��3)��Pr({��: X(��)��3})��1/20
�@�@�@Pr(X��2)��Pr({��: X(��)��2})��9/20
�@�@�@Pr(X��1)��Pr({��: X(��)��1})��9/20
�@�@�@Pr(X��0)��Pr({��: X(��)��0})��1/20
�ł���B�Ƃ���ŁA�W�{���́u��b���v�w�v�̒P�ʎ擾�҂̊�����P�ŕ\���ƁAP��
�@�@�@P��X/3
�Œ�`����A0, 1/3, 2/3, 1 �̂����ꂩ�̒l���Ƃ�B����ƁA��̎�����
�@�@�@Pr(P��1)��Pr(X��3)��1/20
�@�@�@Pr(P��2/3)��Pr(X��2)��9/20
�@�@�@Pr(P��1/3)��Pr(X��1)��9/20
�@�@�@Pr(P��0)��Pr(X��0)��1/20
�ƂȂ�B�܂�AP���m���ϐ��ƂȂ�B����ʓI�Ȕ䗦�ɂ��Ă̊m���̌v�Z�ɂ��ẮA�t�����Q�Ƃ̂��ƁB
�@�������ɑ����悤�B�u���p���v�w�v�̎��Ƃ��n�߂�ɓ����āA���Ƃ̃��x����ݒ肷�邽�߂ɁA�u���p���v�w�v�𗚏C���Ă���6�l�̊w���̒�����A����������g���āA3�l��W�{�Ƃ��Ē��o(�����o)���A����3�l�ɂ��Ċe�X���O�Ɍ����������s�����B���̌��ʁA3�l�Ƃ��u��b���v�w�v�I�����Ɠ����ȏ�̒m���������Ă��邱�Ƃ��킩�����B�������A���ɁA�u��b���v�w�v�Ɠ����ȏ�̒m���������Ă���҂��A�u���p���v�w�v�̗��C��6�l�̂����A���傤�ǔ�����3�l�����������Ƃ��Ă��A���o�̃v���Z�X�ŁA���R�A����3�l�𒊏o���Ă��܂��A���������������ʂ������邱�Ƃ����肤��B���̏ꍇ�A����ג��o�ŕW�{���o�����̂ŁA�e�W�{�_�̂ǂ�������o�����͓̂����x�Ɋm���炵���A���̊m���́A�e�ՂɌv�Z���邱�Ƃ��ł���B���Ȃ킿
�@�@�@Pr(P��1)��Pr(X��3})��1/20��0.05
�ƂȂ�B���������āA���Ɂu��b���v�w�v�Ɠ����ȏ�̒m���������Ă���҂��A�u���p���v�w�v�̗��C��6�l�̂����A���傤�ǔ�����3�l�����������Ƃ������Ƃ��{�����Ƃ���ƁA�W�{�S�����u��b���v�w�v�I�����Ɠ����ȏ�̒m���������Ă����Ƃ����m���́A�킸��5%�����Ȃ��Ƃ������ƂɂȂ�B���̒�m���ł́A��W�c��3�l�������u��b���v�w�v�Ɠ����ȏ�̒m���������Ă����Ƃ͍l���ɂ����ł��낤�B
�@���̂��Ƃ��A��������̌��t���g���ƁA���̂悤�ɋL�q���邱�Ƃ��ł���B�܂��ŏ��ɁA
�@�Ƃ���ŁA��W�c�ł���u���p���v�w�v�̗��C�ґS�̂̂����A�u��b���v�w�v�Ɠ����ȏ�̒m���������Ă���҂̔䗦���ŕ\���ƁA�����قǂ̉����́A
�@��W�c�ł̓�0.5�������̂ɁA���R�A�W�{�ł�P��1�ɂȂ��Ă��܂����Ƃ����ꍇ�́u���R�v�̕������m���ŕ\���������̂�L�ӊm���Ƃ����B���������āA�L�ӊm�����傫���Ƃ��ɂ́A�W�{�ł�P��1�́u�悭������R�v�ƕЕt���Ă��܂��Ă��܂�Ȃ��B���̂悤�ȋ��R�́A�W�{���o�̃v���Z�X�Ŕ�����������̂ŁA���v�I�ɂ͂悭���邱�ƂŁA�Ӗ��̂Ȃ����̂ł���B�܂�A�W�{�덷�͈͓̔��Ƃ����킯�ł���B�������A��قǂ̂悤�ɁA5%�ƗL�ӊm������������A�W�{�ł�P��1�́u�߂����ɂȂ����R�v�ł���B���̂Ƃ��́A�W�{�덷�ł͕Еt����ꂸ�A���v�I�ɂ������ł��Ȃ��Ӗ��������ƂɂȂ�B���̂��Ƃ��u���v�I�ɗL�Ӂv���邢�͒P�Ɂu�L�Ӂv(significant)�Ƃ����B���̏ꍇ�ɂ́A�t�ɁA��W�c�Ń�0.5�Ƃ��������̕����^���ׂ��ł���ƌ��_�Â���̂���������̊�{�I�l�����ł���B�܂�A��0.5�ł͂Ȃ��āA��0.5�ł��낤�Ɣ��f����̂ł���B
�@�ȏ�̂��Ƃ�����ƁA���v�I�����Ƃ́A��W�c�̓����l�A���Ƃ��A�䗦�A���邢�́A��3�͈ȍ~�Ő������镽�ρA���U�A���W���Ȃǂɂ��ė��Ă��鉼���̂��Ƃł���B������������H0�́u���p����v(�����ɋA��)���߂ɐݒ肳�ꂽ���̂ł���A���̂��Ƃ���A������(null hypothesis)�Ƃ���B���̂悤�ɉ�������ł́A��W�c�̓����l�Ɋւ���A���������^�ł���Ƃ��ɁA����ɑΉ�����W�{�̒l�̐��N����m�����A�L�Ӑ���(level of significance; 5%���悭�g����)�ɖ����Ȃ��Ƃ��A����͋A���������^�łȂ��Ɣ��f����ɏ\���ȏ؋��ƍl����̂ł���B(�����K���1.2)
�@����ג��o�@���Ƃ�Ƃ��A�W�{�̑傫��(sample size)�́A�W�{�덷���ǂ̒��x�ɗ}���������Ō��߂���ׂ����̂ł���B�W�{�����̏ꍇ�A�덷�́A�t�ɐ��x�Ƃ����T�O�ōl�@�����B�W�{�����ɂ����āA���̂悤�ɂ��Ď��O�Ɍ��߂����x�̂��Ƃ�ڕW���x�ƌĂԁB
�@���ܔ䗦�̐�����l���悤�B�傫��n�̕�W�c�̂���A�Q�ł����W�c�䗦���Ƃ���B���̕�W�c���疳��ג��o�@�ɂ���āA�傫��r�̕W�{�𒊏o���A���̂���A�Q�ł���W�{�䗦��P�Ƃ��悤�B����ג��o���s���Ă���̂ŁA�W�{�䗦P�͊m���ϐ��ƂȂ�B
�}1.5�@��W�c�䗦�ƕW�{�䗦
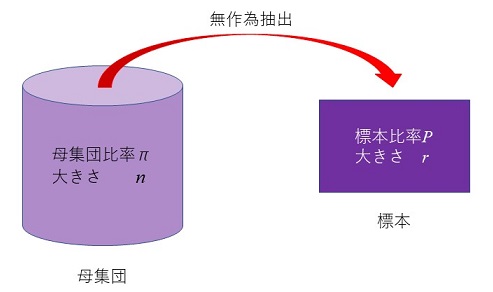
�@�W�{�̑傫��r���A�ق�50����傫���ł���Ȃ�A���S�Ɍ��藝�ɂ���āA�W�{�䗦P�͎��̊��Ғl�A���U�������K���z�ɂ��������m���ϐ��ƂȂ邱�Ƃ��m���Ă���B
�@�@�@����: E(P)����
�@�@�@���U: V(P)��{(n�|r)��(1�|��)}/{(n�|1)r}
���������āA��ʂɐ��K���z�ɏ]���A
�@�@�@Pr({�|1.96(V(P))1/2��P���{1.96(V(P))1/2})��0.95
��������̂�(��3�͑�7���Q�Ƃ̂���)�A���̎���ό`����
�@�@�@Pr({P�|1.96(V(P))1/2����P�{1.96(V(P))1/2})��0.95
�ƂȂ�B�܂�A��W�c�䗦���W�{�䗦P�}1.96(V(P))1/2�ȓ��Ɏ��܂�m����95%���Ƃ������ƂɂȂ�B����������A�M���x95���ŕ�W�c�䗦�𐄒肷�邱�Ƃ��ł���̂ł���B(���̂Ƃ��A��� [P�|1.96(V(P))1/2, P�{1.96(V(P))1/2] �͐M���W��(confidence coefficient) 95����P�̐M�����(confidence interval)�Ƃ���B)
�@���̂Ƃ��A����̌덷�̐�Βl��
�@�@�@�Á�1.96(V(P))1/2�@�@�@(1.2)
�Ƃ����ƁA�Â͐�ΐ��x(absolute precision)�Ƃ�����̂ɂȂ�B���x�̍����������邢�͐���Ƃ́A����̕���1/2�ɑ�������Â̏��������̂�����(�������A�P�Ɂu���x�v�Ƃ������ꍇ�ɂ́A�W�{���U�̋t���Œ�`�����̂Œ��ӂ���)�B���̂悤�ɁA��W�c�̓����l��������̊m���ȏ�Ŏ��܂��Ԃ����߂鐄��@�́A��Ԑ���@(interval estimation)�Ƃ���B
�@�W�{�̑傫��r���傫���Ȃ�ق�V(P)�����ăÂ͏������Ȃ�̂ŁA�K�v�ȕW�{�̑傫��s�́A�ڕW���xd�ɑ��āA�Á�d�ƂȂ�悤�ȍŏ��̕W�{�̑傫���ł���Bs�́A(1.2)����r�ɂ��ĉ�����
�@�@�@r��n/����
�@�@�@���ꁁ(��/1.96)2[(n-1)/{��(1-��)}]�{1�@�@�@(1.3)
�ŃÁ�d�Ƃ����ċ��߂�r�ȏ�̍ŏ��̐����ł���B
�@��ʂɁA��W�c�䗦�͖��m�Ȃ̂ŁA��0.5 �Ɖ��肷��B�Ȃ��Ȃ�A���̂Ƃ�(V(P))1/2�͍ő�ɂȂ�̂ŁA��0.5 �Ɖ��肵�Ă����A�덷���ő�Ɍ��ς��������ƂɂȂ邩��ł���B(1.3)���̒��̃�(1�|��)���A��0.5�̂Ƃ��ő�ƂȂ�B�ڕW���x��d��0.05 (5%)���x�ɂ��邱�Ƃ��l����ƁA�K�v�ȕW�{�̑傫��s�́A(1.3)����p����A�\1.7(a)�̂悤�ɂȂ�B�����A�ڕW���x��d��0.025 (2.5%)�ɏグ�悤�Ƃ���ƁA�\1.7(b)�̂悤�ɂȂ�B
�\1.7�@�ڕW���x�ƕW�{�̑傫��
(a)�ڕW���xd��0.05 (5%)�̂Ƃ��ɕK�v�ȕW�{�̑傫��(�ߎ��l)
| n | 50 | 100 | 1,000 | 2,000 | 5,000 | 10,000 | 20,000 | 50,000 | �� |
|---|---|---|---|---|---|---|---|---|---|
| s | 45 | 80 | 278 | 323 | 357 | 370 | 377 | 382 | 384 |
(b)�ڕW���xd��0.025 (2.5%)�̂Ƃ��ɕK�v�ȕW�{�̑傫��(�ߎ��l)
| n | 50 | 100 | 1,000 | 2,000 | 5,000 | 10,000 | 20,000 | 50,000 | �� |
|---|---|---|---|---|---|---|---|---|---|
| s | 49 | 94 | 607 | 870 | 1176 | 1332 | 1427 | 1492 | 1537 |
�@�\1.7��(a)��(b)���r����ƁA���x���グ�Ă��̕���1/2�ɂ���̂ɂ́A�W�{�̑傫�����4�{�ɂ��Ȃ���Ȃ�Ȃ����Ƃ��킩��B��ʂɁA�ڕW���xd��1/k�{�ɂ��悤�Ƃ���ƁA�K�v�ȕW�{�̑傫���͖�k2�{�ɂȂ�B�Ȃ��Ȃ�(1.3)���̕���Ƀ�2�����邩��ł���B�܂������̐��x�́A��W�c�̑召�ɂقƂ�NJW�Ȃ��A�W�{�̑傫���̕������ɂقڔ���Ⴗ��B����������50�l���x�̕�W�c�ł́A�W�{�����Ƃ����Ă��A�قƂ�ǑS���������K�v�ɂȂ����ŁA�ǂ�Ȃɕ�W�c���傫���Ă��A�ڕW���x��5%�Ȃ��400�l���x�A�ڕW���x��2.5%�ł�1600�l���x�̑傫���̕W�{�ł���A�\���ɖڕW��B������B
�@�Ƃ���ŁA�W�{�̑傫����400���x����A��ΐ��x��5%�ȉ��ɗ}������Ƃ������Ƃ́A�t�ɂ����A���Ƃ��ΕW�{�䗦��56%�ł���A��W�c�䗦��50%�ł���m����5%(��1�|�M���W��)�ȉ��Ƃ������Ƃł���B�܂�AH0: ��0.5 �Ƃ��������́A����������s���Ί��p����邱�ƂɂȂ�B��������ς���A5%���x�̔䗦�̍������v�I�ɗL�ӂɂȂ�A�Ӗ������悤�ɁA�W�{�̑傫�������߂Ă���Ă��邱�ƂɂȂ�B���̂悤�ɁA�W�{�̑傫�����\���ɑ傫���āA���x���\���Ɍ��サ�Ă���A���͂₢��������������ɋC���K�v�͂Ȃ��B�������ɁA�������W�{�̃f�[�^��^�����Ă���Ƃ��ɂ́A��������ŕ�W�c�ɂ��Ă̒m���������E�ᖡ����K�v������B�������A�\���ȑ傫���̕W�{���m�ۂ��邱�Ƃ��ł����Ȃ�A�������肪���ۏ�K�v�Ȃ��قǁA����̐��x���m�ۂł������ƂɂȂ�̂ł���B
�@����܂ł̋c�_���A���ۂɒ�����v���A�Ǘ�����Ƃ����ϓ_����܂Ƃ߂�ƁA���̂悤�ɂȂ�B�����ɂƂ��Ȃ��덷���l���A�W�{�덷(��Ό덷)�Ɣ�W�{�덷���Ƃ���5%�ȓ��ɗ}����Ƃ������Ƃ��߂����̂ł���A�W�{�̑傫���Ƃ��Ă�500���x�m�ۂ�(���������āA���S���x�̑傫���̕�W�c�łقƂ�ǑS���������K�v�ɂȂ�)�A�����80%�ȏ���߂����āA���߂ׂ̍����Ǘ������邱�Ƃ��l����ׂ��ł���B
�@�䗦�ɂ��Ă̗L�ӊm���̌v�Z�́A��ʓI�ɂ͂ǂ̂悤�ɍs����̂ł��낤���B���܁An�̗v�f����Ȃ��W�c���l����B���̕�W�c�̗v�f�́AA�Q�A��A�Q��2�Q�ɕ��ނ���A�e�v�f���ǂ���̌Q�ɑ����邩�͊ȒP�ɋ�ʂł���Ƃ���B
�@���̕�W�c��������o(sampling without replacement)�ŁAr��W�{�Ƃ��Ē��o���邱�Ƃ��l���悤�B�܂�Ar�̂��̂����o���Ƃ��ɁA1���Ƃɂ����������ɖ߂����ɁA������r�����o�����Ƃ��l����B
�}1.6�@�L����W�c����̒��o
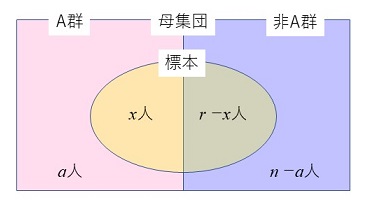
�@�m���ϐ�X�ő傫��r�̕W�{�̂����AA�Q�ɑ�����v�f�̐���\�����̂Ƃ���B�����
�@�Ƃ���ŁA�W�{�ł�A�Q�̔䗦P��x/r�́A��W�c��A�Q�̔䗦����a/n�ɓ������Ȃ肻���Ȃ��̂����A����ג��o������A���R�̂�������ŁAP��0�`1�܂ł̒l���Ƃ肤��\��������(�������A�W�{�̑傫���ɔ�ׁA��W�c���\���ɑ傫���Ƃ�)�B�������A�������܂��������A�m���ϐ��ł���W�{�䗦P�̂Ƃ肤��l���A�m�����E�F�C�g�Ƃ��ĉ��d���ς����l(��������Ғl�Ƃ���)�͕�W�c�䗦�ɓ������Ȃ�B���ہA(1.5)���ŕ\�����ꍇ�̒����z�̕���(�����Ғl)�A���U�͎��̂悤�ɂȂ�B
�@�@�@����: E(P)����p p�h(p)����
�@�@�@���U: V(P)��{(n�|r)��(1�|��)}/{(n�|1)r}
���̂悤�ɁA�W�{�䗦�̊��Ғl����W�c�䗦�ƈ�v����ꍇ�A�W�{�䗦�͕�������Ȃ�(���s��)�Ƃ�����B
�@����܂ł́An�̗v�f����Ȃ�L����W�c��������o���s�����Ƃ��l���Ă����B���܂����An�����ɑ傫���Ƃ��A�ɒ[�ɂ͖����ɑ傫���ƍl������Ƃ��͂ǂ��Ȃ�ł��낤���B(1.4)������
�@�@�@h(x)��[(n��)(n��-1)���(n��-(x-1))/x!]�~[(n(1-��))(n(1-��)-1)���(n(1-��)-(r-x-1))/(r-x)!]�~[r!/{n(n-1)���(n-(r-1))}]
�ƂȂ�A���̎��̕��ꕪ�q��nr�Ŋ����
�@�@�@h(x)��[r!/x!(r-x)!]�~[{��(��-1/n)���(��-(x-1)/n)�E(1-��)((1-��)-1/n)���((1-��)-(r-x-1)/n)}/{1�(1-1/n)���(1-(r-1)/n)}]
�ƂȂ�B���������āA�����z�� n�����̂Ƃ�
�@�@�@limn���� h(x)��rCx��x(1-��)r-x��b(x)
�ƂȂ�B���̕��zb(x)�͓��z(binomial distribution)�Ƃ���B���̕��z�̖��O�̂����́A��
�@�@�@(��+(1-��))r
��W�J�����Ƃ��A��x(1-��)r-x�̍��̌W����rCx�ɂȂ��Ă��邱�Ƃɂ��B�ȏ�̂��Ƃ���A��W�c�̑傫��n���傫���Ƃ��ɂ́A�����z����z�ŋߎ����邱�Ƃ��ł���B
�@���z�́A������W�c����̒��o�����ł͂Ȃ��A���Ƃ��L����W�c�ł����Ă��������o(sampling with replacement)�A�܂�1���o�����Ƃɂ����������ɖ߂��Ȃ���r�̕W�{�����o���Ƃ��ɂ�������B�Ȃ��Ȃ�A�ǂ���̏ꍇ�ɂ��A��W�c����1�v�f�����o�����Ƃ��ɁA���ꂪA�Q�ł���m���̓A��A�Q�ł���m����1-�ŁA����͒��o�ɂ�����炸��肾����ł���B���������āAA�Q��x�A��A�Q��r-x�ł����A���Ƃ���
�@�@�@AA(��A)A�c�c(��A)A
��������m����
�@�@�@��(1-��)�c�c(1-��)����x(1-��)r-x
�ł���B���̎�������킩��悤�ɁAA�Q�Ɣ�A�Q�̗v�f�̕��ԏ����ɂ͊W�Ȃ��A�`�Q��x�A��A�Q��r-x�ł���W�{�_�́A�����m���������ƂɂȂ�B���������āA����Ɠ����m�������W�{�_�́A�W�{��Ԃ̒��� rCx����̂ŁA���ʂƂ���
�@�@�@rCx��x(1-��)r-x��b(x)
�Ƃ������z��������킯�ł���B
1.1 �����̎�� �@��3��(1)�Ő����������ނɂ��������āA�{���œ��v�����̎���Ƃ��Ď��グ�Ă���u�g�D�������̂��߂̏]�ƈ��ӎ������v�̎�ނނ��Ă݂�B�K�v�ł���A��6�����ǂ�ł݂邱�ƁB
1.2 �������� �@��6���̗�ŁA�������������̌��ʁA�W�{3�l�̂���2�l�������u��b���v�w�v�I�����Ɠ����ȏ�̒m���������Ă��邱�Ƃ��킩�����Ȃ�A���̂Ƃ����� H0: ��0.5 �̌�����s�Ȃ��Ă݂�B
1.3 ���ꂽ�������ʂ̕]�� �@�ŋ߁A�V���ŕ��ꂽ�������ʂ��ȏ�T���A���̒������ʂɂ��āA(1)��W�c�̒�`�A(2)�S���������W�{�������A(3)�W�{�����̏ꍇ�ɂ͕W�{���o�̕��@�A(4)�������_�A(5)�������@�A(6)������ׂ�B
1.4 �����̊�� �@�u�V�l�ސ���̈ӎ���T��v�Ƃ����e�[�}�ŁA�]�ƈ��K��(���Ј��̂�) �P���l���x�̊�Ƃ̈ӎ��������������B�ǂ̂悤�Ȓ��������ׂ������𗧂Ă�B
�@��1�͂ł͓��v�w����ђ����̍l�������T�ς����̂ŁA���̏͂���͂��������u�g�D�������̂��߂̏]�ƈ��ӎ������v�ɂ���ē���ꂽ�f�[�^��f�ނɂ��āA�R���s���[�^���g���ē��v�������邱�Ƃ��n�߂悤�B���̂��߂ɁA���̏͂ł͂܂����v�p�b�P�[�WSAS�̊�{�I�Ȏg�������A�ŏ��ɂ��ׂ���{�I���v�����ł���P���W�v���ɐ������Ă������Ƃɂ���B
�@SAS�̓f�[�^�ɑ��āA���v�����E���Z�������n�߂Ƃ���e��̉��H�������s���p�b�P�[�W�E�v���O�����ł���B��������ꂪ�e��̓��v�����p�ɂ��ꂼ��̃v���O�����������ō쐬�E�J���E�ێ����悤�Ƃ���ƁA����͔��ɑ�ςȍ�ƂƂȂ�B���̓_SAS�́A���Ɋ�������Ă��铝�v�p�v���O�����̏W���́A�V�X�e���ł���A���p�҂��K�v�ȃv���O�������w�肷��ƁA�������@�\�I�Ƀf�[�^�Ɍ��ѕt���āA���v���������Ă����̂ł���B
�@���̏͂ł́A�ŐV�łł���SAS��6�ł̎g�����ƃv���O���~���O��SAS��R���s���[�^��S���m��Ȃ��ǎ҂ł������ł���悤�ɉ�����邱�Ƃɂ��悤�B�������A�P�Ȃ�SAS����ł͂Ȃ��A�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̃v���Z�X��1�X�e�b�v�Ƃ��āA�����ɂ���ē���ꂽ�f�[�^��P���W�v���A��̏͂ł̓��v���͂̂��߂Ƀf�[�^���f�[�^�E�x�[�X�����Ă����̂��A���̖̏͂{���̖����ł���B
�@�{���ł̓p�[�\�i���E�R���s���[�^��SAS�A������PC��SAS�ƃ��C���t���[��(mainframe)��SAS�̗����ɂ��āA����Η��������I�ɑ���_�Ȃǂɂ����y���Ȃ���������Ă����B����́A����M�҂��܂߂đ����̐l���ASAS���g���ہA�������Ԃ�R�X�g�A���p�\�������l��������ŁA�p�[�\�i���E�R���s���[�^�ƃ��C���t���[�����g�������A�����v���O�����A�f�[�^���t���b�s�B�E�f�B�X�N1���ňڐA���A�ǂ���̋@�B�ł��g�����ƂɂȂ��Ă����ƍl���邩��ł���B�Ƃ͂������̂́A�ǂ��炩�Ƃ����APC��SAS�𒆐S�ɂ��āA���̎g�����𑀍�̏����ɂ��������Đ�������B����̓I�ɂ́AMS-DOS�𓋍ڂ����p�[�\�i���E�R���s���[�^�ɁA����SAS�̑�6��(�����[�X6.04)���C���X�g�[������Ă��邱�Ƃ�O��ɂ��āA�b��i�߂邱�Ƃɂ��悤�B
�@���C���t���[�����p�҂ɑ��ẮASAS��6�ł�IBM�y��IBM�݊��̍��Y�̃��C���t���[���ł����p�\�Ȃ̂ŁA���C���t���[����SAS�Ƃ���IBM���C���t���[���̑�\�I��OS�ł���CMS�ɑΉ����Ă���CMS��SAS (SAS�����[�X6.06)�ɂ��Ă��APC��SAS�Ƃ̑���_�Ȃǂ��w�E���Ȃ��畹���Đ������Ă����B�܂��A���݂ł��A���C���t���[���̈ꕔ�ł́ACMS��SAS�����[�X5.18�����̂܂g�p����Ă���悤�Ȃ̂ŁA�t����݂��ACMS��SAS�����[�X5.18�̊�{�I�Ȏg�p���@�ɂ��āA��6�łƂ̈Ⴂ���T�����Ă������B
�@�����Ƃ��ASAS��6�łł́A���C���t���[���p���p�[�\�i���E�R���s���[�^�p���Ƃ���C����ŏ�����A�g�p���@�͊�{�I�ɓ����ł���B�t�@�C�����̌`���Ɖ�ʂ̃E�B���h�E�̐����قȂ邱�Ƃɒ��ӂ���APC��SAS��CMS��SAS�����l�Ɏg�p���邱�Ƃ��ł���B�������ACMS��SAS�́A���̃��C���t���[���pSAS�Ɣ�r���Ă��A�n�[�h�E�F�A��\�t�g�E�F�A�ɂ��Ă̗]�v�Ȓm����z����K�v�Ƃ��Ȃ��Ƃ����_�ł́A�p�[�\�i���E�R���s���[�^���̎g���₷�����������V�X�e���ł���B�Ⴆ�A�ʏ�A���C���t���[���ł�SAS�̂悤�ȃp�b�P�[�W�E�\�t�g�ł����Ă��A���ۂɓ����悤�ɂ��邽�߂ɂ́A�n�[�h�E�F�A�̎d�l�A�\�t�g�E�F�A�̎d�l�A����ɓ��������Ƃ��Ă���v���O�����̎d�l��f�[�^�̃T�C�Y�Ȃǂ��z��������ŁA���܂��܂Ȋ��ݒ���s���K�v������B���̐ݒ���s���̂�JCL (job control language�A�u�W���u�R���v�ƌ������Ƃ�����)�ƌĂ����̂ł��邪�A���̂悤�ɁA�\�t�g�̎g�p�ɍۂ��āA���p�҂���������Y�܂���Ă���JCL�ɂ��Ă��ACMS��SAS�ł͈�؋C�ɂ���K�v�͂Ȃ��BCMS�ł́A���O�I������PROFILE�Ƃ������O�̏����ݒ�t�@�C���������I�ɋN������A���p�҂̊��ݒ肪�����I�ɍs���Ă��܂��̂ł���B
�@����ł́APC��SAS���g�p�����ŕK�v�ɂȂ�ŏ�����MS-DOS�̊�b�m���ɂ��Ă̐�������n�߂邱�Ƃɂ��悤�BIBM���C���t���[����CMS�ɂ��ẮA�t�����Q�Ƃ��Ăق����BCMS��SAS�̗��p�҂́A���̑�2�߂̑���ɁA�����t����ǂ�ł���A��3���ɐi�ނ��ƁB���C���t���[����CMS�ȊO��OS�Ŏg�p����ꍇ�ɂ́A�Z���^�[���ɖ₢���킹�āASAS���p�ɂǂ̂悤��JCL���K�v�ɂȂ�̂������炩���ߊm�F���Ăق����B
�@OS (Operating System)�Ƃ́A�ȒP�Ɍ����A�O���L�����u����o�͑��u�Ƃ������n�[�h�E�F�A�𑀍삷��\�t�g�E�F�A�̂��Ƃł���B���p�ҁA���邢�͗��p�҂����ڐG��鍂������(�Ⴆ��C����)�A�p�b�P�[�W(�Ⴆ��SAS)��OS�̎g���������Ă���A�O���L�����u����o�͑��u�Ƃ������n�[�h�E�F�A���I�ɒ��ڑ��삷��K�v�͂Ȃ��AOS�Ƃ����\�t�g�E�F�A��̘_���I���u(logical device)�̊ȒP�ȑ�������邾���ŁA���ۂ̊O���L�����u����o�͑��u�̕��G�ȑ����OS������ɂ���Ă����B
�@������X�����G�ȃR���s���[�^�E�V�X�e���̑S�̂��\�����邻�ꂼ��̊O���L�����u����o�͑��u�Ƃ������n�[�h�E�F�A���I�ɒ��ڑ��삵�悤�Ƃ���Ȃ�A�e���u�̋@�B�I�Ȏd�g�݂⌴���𗝉����A�Ȃ����ǂ̂悤�ɑ��삷��̂������Ƃ������I�ŊԈႢ���Ȃ��̂����K�����Ă����Ȃ��Ă͂Ȃ�Ȃ��B�l���������ŋC�̉����Ȃ�悤�Șb�ł���B�p�[�\�i���E�R���s���[�^�ł���AMS-DOS�̂悤��OS�Ȃ��Ńn�[�h�E�F�A���I�ɒ��ڑ��삷�邱�Ƃ͕s�\�ł���B���ꂾ��OS�͕֗��ł���A���R���s���[�^�E�V�X�e���̎g������A���p���������߂�Ƃ����_�Ō���I�ɏd�v�Ȃ��̂ł���B
�@�����ł����ł́A�p�[�\�i���E�R���s���[�^�̃n�[�h�E�F�A�ɂ��Ă͐G�ꂸ�AOS�ł���MS-DOS�ɂ��āASAS���p�̂��߂ɍŏ����K�v�Ȃ��Ƃ���ɂ��Đ������Ă������B
�@�t�@�C��(file)�܂��̓f�[�^�E�Z�b�g(data set)�Ƃ́A�����I�ɂ̓R���s���[�^�E�V�X�e���̌Œ�f�B�X�N��t���b�s�B�E�f�B�X�N�Ɋi�[���ꂽ�v���O������f�[�^�̏W���̂��Ƃł���B����̓I�ɂ́A�p�[�\�i���E�R���s���[�^��C���t���[���̒[���̃f�B�X�v���C��ʂ̏�ɓ��́A�\�����ꂽ�s�̏W�����f�B�X�N�Ɋi�[�������̂��t�@�C���ł���B�f�B�X�N�ɕۑ����ꂽ���́A���̃t�@�C���Ƃ����P�ʂŊǗ������B(�ڍׂ��t�͑�1�����Q�Ƃ��ꂽ���B)
�@�t�@�C���ɂ͂��ꂼ�ꖼ�O���t�����A���̃t�@�C���Ǝ��ʂ����BMS-DOS�̃t�@�C�����́A�Ⴆ�Ύ��̂悤�Ȍ`�����Ă���B
�@�@�@FRQ.LOG
�@�@�@JPCDATA.SAS
�t�@�C�����́A��ʓI�ɂ�
�@�@�@�t�@�C�����{��.�t�@�C�����g���q
�Ƃ����`�����Ƃ��Ă���B�t�@�C�����̖{�̂Ɗg���q�̊Ԃɂ͕K���s���I�h "." �����ނ��ƂɂȂ��Ă���BMS-DOS�̃t�@�C�����̊g���q�͕K���t���Ȃ��Ă͂Ȃ�Ȃ��Ƃ������̂ł͂Ȃ����A�t�@�C���̓��e�̕��ނ̂��߂ɂ͕t���Ă����ƕ֗��ł���B�g���q��t���Ȃ��ꍇ�ɂ̓s���I�h "." �͕t���Ȃ��B
�@�t�@�C�����̋�̓I�ȕ\�L���@�Ƃ��ẮA�t�@�C�����{�̂�8�����ȓ��A�g���q��3�����ȓ��ƂȂ��Ă���A�p����A�`Z�A0�`9�A�����$�A#�A@�A-(�n�C�t��)�A_(����)�̋L���ނ���Ȃ镶����ł���B���̂ق��ɂ��g����L�������邵�A�Ђ炩�ȁA�J�^�J�i�A�������g���邱�ƂɂȂ��Ă��邪�A���C���t���[���Ŏg�p����ꍇ�����邱�Ƃ��l����ƁA�g���u���̌����ɂȂ�̂ŁA���܂芩�߂��Ȃ��B���̈Ӗ��ł́A�t�@�C������1�����ڂ͉p���ɂ��Ă�������������ł��낤�B�܂��A�p���ɑ啶���A�������̋�ʂ͂Ȃ��AMS-DOS�ł́A���ׂđ啶���ɕϊ�����ď��������B
�@�V���Ƀt�@�C���������ꍇ�ɁA�����A���ɑ��݂��Ă���t�@�C���Ɠ����t�@�C������t���悤�Ƃ���ƁA�����炠��t�@�C���̓��e������ꂽ��A�G���[���o���肷�邱�ƂɂȂ�̂ŁA���ӂ��K�v�ł���B
�@�Œ�f�B�X�N����ւ��\�ȃt���b�s�B�E�f�B�X�N�Ƃ������u1���v�̃f�B�X�N�̒��ɂ́A�����̃t�@�C�����i�[���邱�Ƃ��ł���B�����ŁAMS-DOS�ł̓f�B�X�N�̒��̂ǂ��ɂǂ�ȃt�@�C�����i�[����Ă��邩�A�f�B���N�g��(directory=�Z���^)������ĊǗ����Ă���B�������A�ڂ����u�Z���v��MS-DOS�̃V�X�e���ɂƂ��Ă͕K�v�ȏ���A���p�҂ɂƂ��Ă͕K�v�Ȃ��̂ŁA���p�҂ɂ͕\������Ȃ��B���̃f�B���N�g���̒��ɂ́A�t�@�C�������ł͂Ȃ��A�ʂ̃f�B���N�g��������邱�Ƃ��ł���B���̃f�B���N�g����e�Ƃ���A���̈ꗗ�\�̒��ɕ\�L����q�̊W�ɂ���f�B���N�g�����T�u�f�B���N�g���ƌĂԁB���̃T�u�f�B���N�g�������ꎩ�̂��e�f�B���N�g���ƂȂ��āA�T�u�f�B���N�g���������Ƃ��ł���B���̂悤�ɂ��āA���傤�ljƌn�}�̂悤�ɊK�w�f�B���N�g���\�����`�������̂ł���B�܂�A�����̃f�B���N�g�����A���ꂼ�ꑼ�̃f�B���N�g���Ƃ̐e�q�W�������1���̉ƌn�}�Ɏ��܂邱�ƂŁu1���́v�f�B�X�N��ɑ��݂�����킯�ł���B
�@�Ⴆ�A�{���ł�SAS�́w�����y�щ^�p�ƕێ�̎�����x�ʂ�̃f�B���N�g���\����O��ɂ��Ă��邪�A���̍\���͐}2.1�̂悤�ɂȂ�B�Œ�f�B�X�N(�h���C�uA)�̓��e��SAS�̉ғ��ɕK�v�ȍŏ����̃t�@�C���\���ɂȂ��Ă���BSAS�́w�����y�щ^�p�ƕێ�̎�����x�ɂ��������āASAS�̎��s�t�@�C���Ȃǂ�[�߂�SAS�f�B���N�g�����烆�[�U�[�E�v���O�����A�f�[�^�Ȃǂ�[�߂��f�B���N�g������ʁA�������āA�u��MYDIR�v�Ƃ������p�f�B���N�g�����쐬���Ă���B����́ASAS�̃o�[�W�����A�b�v�̍ۂ̍�Ƃ��y�ɂ��A�����̐l�������Œ�f�B�X�N���g�p����ۂɓƗ������m�ۂ��邱�ƂȂǂ�ړI�ɂ��Ă���B
�}2.1 �Œ�f�B�X�N�̃f�B���N�g���̍\���}
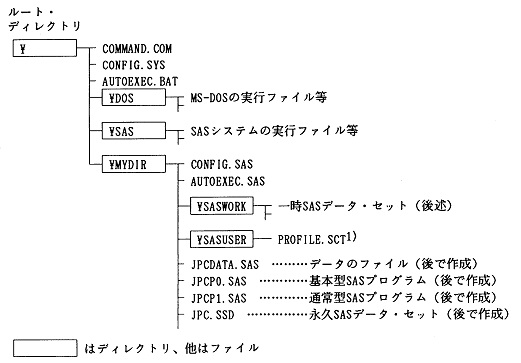
1) �f�B�X�v���C�E�}�l�[�W��(��q)�̊e��ݒ�ۑ��t�@�C�������A�{���ł͏o���̐ݒ��O��ɂ��Ă���̂ŁA����ȏ�G��Ȃ��B
�@�������A���p�҂���x�Ɏg�p�ł���f�B���N�g���͈�ƌ��߂��Ă���B���ݎg�p���̃f�B���N�g�����J�����g�E�f�B���N�g���ƌĂԂ��A���݂ǂ̃f�B���N�g�����g�p���Ă���̂��A�J�����g�E�f�B���N�g�����m���߂�ɂ́Achdir�R�}���h���g���悢�B
�@�@�@A>ChDir
�Ɠ��͂���ƁA�J�����g�E�f�B���N�g�����\�������B�Ⴆ�A�\����
�@�@�@A:��
�Ȃ�A���[�g�E�f�B���N�g�����J�����g�E�f�B���N�g���ł���A�����\����
�@�@�@A:��MYDIR
�Ȃ�AMYDIR���J�����g�E�f�B���N�g���ł���B
�@�J�����g�E�f�B���N�g���͕ύX���邱�Ƃ��ł���B�J�����g�E�f�B���N�g������1�K�w��̐e�f�B���N�g���ɃJ�����g�E�f�B���N�g����ς���Ƃ��ɂ́A��͂�chdir�R�}���h���g���A���̂悤�ɓ��͂���B
�@�@�@A>ChDir ..
�t�ɁA�J�����g�E�f�B���N�g���̃T�u�f�B���N�g���̈�ɃJ�����g�E�f�B���N�g����ς���Ƃ��ɂ́A
�@�@�@A>ChDir �T�u�f�B���N�g����
�Ɠ��͂���悢�B�Ⴆ�A���܃��[�g�E�f�B���N�g�����g�p���Ă���Ƃ���ƁA
�@�@�@A>ChDir MYDIR
�Ɠ��͂���ƁA�T�u�f�B���N�g��MYDIR�Ɉڂ邱�Ƃ��ł���B
�@�J�����g�E�f�B���N�g���̒��ɁA�ǂ�ȃt�@�C����T�u�f�B���N�g�������݂��Ă��邩�A���̈ꗗ�\��\��������Ƃ��ɂ́A
�@�@�@A>DIR
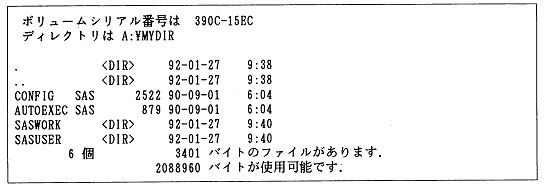
�Ɠ��͂���悢�B����ƃJ�����g�E�f�B���N�g����MYDIR�̂Ƃ��́ASAS�C���X�g�[������ł́A�{�͂̒��ł��ꂩ��쐬����SAS�v���O�������͂܂����݂��Ȃ��̂ŁA�Ⴆ�ΐ}2.2�̂悤�ɂȂ�B
�}2.2 MYDIR�̃f�B���N�g����ʂ̗�(SAS�C���X�g�[������)
�@����(3)�ōs���Ă���悤�ȃL�[�{�[�h����̃R�}���h���͂̐����̍ۂɂ́A�{���ł͎��̂悤�ȕ\�L���@���Ƃ��Ă���B�����ǂ�ŁA������x(3)���������Ă݂�Ƃ悢�B
�@SAS�N���̎d���́APC��SAS��CMS��SAS����{�I�ɓ����ł���BMS-DOS���邢��CMS�̃R�}���h����͂ł��郂�[�h����ASAS �ƃR�}���h���͂̌`�œ��͂��Ă��悢�̂ł���B�������A����͕W���I�ɃC���X�g�[�������ꍇ�ł���ASAS�̃C���X�g�[���̎d��������Ă���A�������N���̎d�������R����Ă���B���Ƀ��C���t���[���ł́A�Ǘ����Ă���Z���^�[���Ƃɂ��Ȃ��������̂ŁA�z�X�g�v�Z�@�̊Ǘ��҂ɕK���m�F���邱�ƁB���́ASAS�̎g�p���@�̂����A�n�[�h�E�F�A�A�\�t�g�E�F�A�A�Ǘ��^�c�V�X�e���ō��ق��o��̂́A����SAS�N���̕��������ł���BSAS����U�N�����Ă��܂���������A��������������Ƃ͈�؊W�Ȃ��A�ǂ̓�����ł������g�p���@��SAS���g�����Ƃ��ł���B�����ł�PC��SAS��W���I�ɃC���X�g�[�������ꍇ�̋N���̕��@���\��Ƃ��Đ������Ă������B
�@����ł́A��������SAS���N�����Ă݂邱�Ƃɂ��悤�B�܂��p�[�\�i���E�R���s���[�^�̓d���X�C�b�`�ł���POWER�X�C�b�`�����āAMS-DOS���N��������B�n�[�h�E�f�B�X�N�E�h���C�u��A�ł���Ƃ��A�v�����v�g���uA>�v�ƂȂ��Ă��邱�ƁA�����āA���p�f�B���N�g��MYDIR���J�����g�E�f�B���N�g���ɂȂ��Ă��邱�Ƃ��m�F������ŁA
�@�@�@A>SAS
�@
�Ɠ��͂����SAS���N�������B
�@SAS�̋N���ɂ���āA�v���O�����쐬�A���s�̂��߂�SAS�f�B�X�v���C�E�}�l�[�W���E�V�X�e��(SAS Display Manager System)�̉�ʂ��\������邱�ƂɂȂ�B���̉�ʂ́APC��SAS�ł͐}2.3�̂悤�ɂȂ�B
�}2.3 PC��SAS�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉��(SAS�N����)

�@PC��SAS�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉�ʂ͐}2.3�����Ă킩��悤��3�̃E�B���h�E�ɕ�������Ă���B�e�E�B���h�E�̖��̂Ɩ����́ASAS�v���O�����̕ҏW�A���s�̎菇�ɂ��������A�����珇���A
�@CMS��SAS�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉�ʂ͐}2.4�Ɏ�����Ă��邪�APC��SAS�ƈقȂ�A��̃E�B���h�E�ɕ�������Ă���BOUTPUT�E�B���h�E��SAS�N�����ɂ͕\������Ȃ��B�����Ƃ��ASAS�N�����ɂ�OUTPUT�E�B���h�E�͕\�����ׂ����e���Ȃ����A�g���p�����Ȃ��̂ŁA���̂��Ƃŕs�ւ͂Ȃ��B
�}2.4�@CMS��SAS�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉��(SAS�N����)
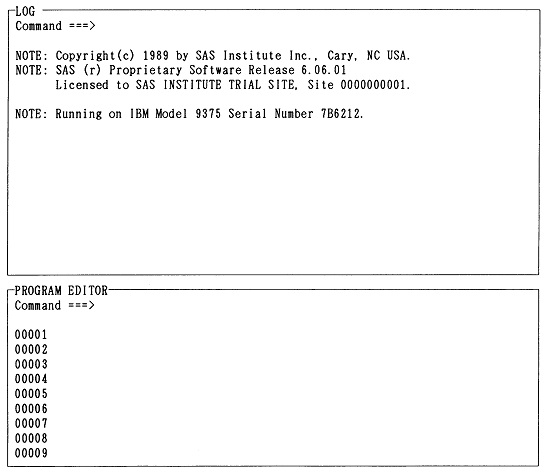
�@PC��SAS�ł���ACMS��SAS�ł���ASAS�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉�ʂ̃t�@���N�V�����E�L�[�ɂ́A���p�҂���r�I�悭�g�p����R�}���h���ݒ肳��Ă���B�t�@���N�V�����E�L�[�ɐݒ肳��Ă���R�}���h�́A�悭�g���R�}���h�Ȃ̂ŁA�R�}���h�Ƃ��Ă��A���̋@�\���悭�������Ă������B�t�@���N�V�����E�L�[�̐ݒ�͗��p�҂̎�ŕς��邱�Ƃ��ł��邪�A�\2.1��PC��SAS�ł̏o���̐ݒ�ł���B���̏͂ł́A�\2.1�̐ݒ��O��ɂ��Ęb��i�߂�B
�\2.1�@�f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉�ʂ̃t�@���N�V�����E�L�[(PC��SAS�o��)
| �@�L�[�@ | �ݒ� �R�}���h | �@�\ |
|---|---|---|
| (f�1) | help | �R�}���h�A�@�\�ɂ��Đ�������HELP�E�B���h�E��\�����A���̃��C���E���j���[��\������B |
| (f�2) | keys | �t�@���N�V�����E�L�[�̐ݒ������KEYS�E�B���h�E��\������B |
| (f�3) | log | LOG�E�B���h�E��\������B���ɕ\������Ă���ꍇ�ɂ́A�J�[�\����LOG�E�B���h�E�Ɉړ�����B |
| (f�4) | output | OUTPUT�E�B���h�E��\������B���ɕ\������Ă���ꍇ�ɂ́A�J�[�\����OUTPUT�E�B���h�E�Ɉړ�����B |
| (f�5) | next | �E�B���h�E�����ԂɃJ�[�\�����ړ�����B |
| (f�6) | prg | PROGRAM EDITOR�E�B���h�E��\������B���ɕ\������Ă���ꍇ�ɂ́A�J�[�\����PROGRAM EDITOR�E�B���h�E�Ɉړ�����B |
| (f�7) | zoom | �J�[�\���̂���E�B���h�E��������ʈ�t�ɕ\������Y�[���E���[�h�ɂ��邩�A�ʏ�̃}���`�E�E�B���h�E�E���[�h�ɂ��邩���ւ���B |
| (f�8) | subtop | PROGRAM EDITOR�E�B���h�E�̑�P�s��SAS�����������s������B���̂��Ƃł��̑�1�s�͏����A��2�s�ȍ~��1�s���J��オ�邱�ƂɂȂ�B |
| (f�9) | recall | PROGRAM EDITOR�E�B���h�E�ɃJ�[�\��������Ƃ��ɗL���ŁA���O�Ɏ��s�����v���O������PROGRAM EDITOR�E�B���h�E��ɌĂяo���B����PROGRAM EDITOR�E�B���h�E�ɓ��e������Ƃ��ɂ́A���̓��e�̎n�߂ɑ}�������Brecall������Ɏ��s����ƁA�O�X��A�O�X�X��A�c�c�Ǝ��X�Ƒk���Ďn�߂ɑ}�������B |
| (f�10) | zoom off; submit | �}���`�E�E�B���h�E��Ԃɂ��Ă���APROGRAM EDITOR�E�B���h�E��̃v���O���������s����B |
�@�܂��A�e�E�B���h�E�ł́A�\2.2�̂悤�ȕҏW�L�[�����̂܂g����B
�\2.2�@�ҏW�L�[(PC��SAS)
| �L�[ | �@�\ |
|---|---|
| (INS) | �}�����[�h�Əd�������[�h���ւ���B�}�����[�h�̂Ƃ��́A��ʉE���[�� "I" �̕������\�������B |
| (DEL) | �J�[�\����̕������폜����B |
| (BS) | �J�[�\���̂P���O�̕������폜����B |
| (ROLL UP) | ��ʂ�����ɃX�N���[�����A����ʂ̓��e��\������B |
| (ROLL DOWN) | ��ʂ������ɃX�N���[�����A�O��ʂ̓��e��\������B |
| (CAPS) | �A���t�@�x�b�g�̑啶�����̓��[�h�Ə��������̓��[�h���ւ���B�啶�����̓��[�h�̂Ƃ��́A��ʉE���[��"C"�̕������\�������B |
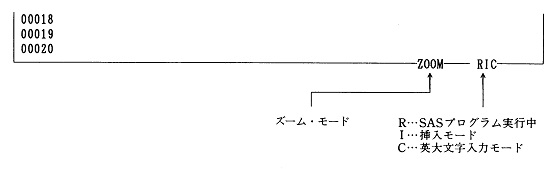
�@�Y�[���E���[�h�A�}�����[�h�A�p�啶�����̓��[�h�Ƃ������A���ꂼ��Ή�����L�[�ɂ���ăX�C�b�`�̂悤��on/off���J��Ԃ����̂ɂ��ẮA�f�B�X�v���C�E�}�l�[�W���E�V�X�e����ʂ̉E���[�̃E�B���h�E�̘g��ɁA�}2.5�̂悤�ɁA���݂̃��[�h�̏�Ԃ��\�������B�����\������Ă��Ȃ��Ƃ��ɂ́A������̏�Ԃł��Ȃ��Ƃ������Ƃ��Ӗ����邱�ƂɂȂ�B
�}2.5�@SAS�̏�ԕ\��(�f�B�X�v���C�E�}�l�[�W���E�V�X�e����ʂ̉E���[�ɕ\��)
�@�t�@���N�V�����E�L�[�̐ݒ�͒ʏ�͉�ʂɂ͕\������Ȃ��̂ŁA�悭�g�p������̂ɂ��Ă͊o���Ă����Ε֗��ł���B���R�͂悭�킩��Ȃ����ACMS��SAS�ł́A�����z�X�g�v�Z�@�ɐڑ����ꂽ�[���ł��A�Ⴆ�A��p�[���ƃp�\�R���[���̂悤�ɁA�[���̋@��ɂ���ďo���̐ݒ���قȂ��Ă���悤�Ȃ̂ŁACMS��SAS�̃t�@���N�V�����E�L�[�̐ݒ�́A�����ňꗗ�\�ɂ��邱�Ƃ͂��Ȃ��B�g�p����ۂɁA�����ł܂�Command�s��
�@�@�@Command ===> KEYS
�Ɠ��͂��āA�m�F���Ă݂邱�ƁB���Ȃ��Ƃ��A�\2.1�ɂ���R�}���h�ɑΉ�����t�@���N�V�����E�L�[�ɂ��ẮA�g���n�߂̂Ƃ��Ɏ����Ń`�F�b�N���Ă������B���ɏd�v�Ȃ̂́ACMS��SAS�ł́A�ҏW�L�[��(ROLL UP)�L�[�A(ROLL DOWN)�L�[���g���Ȃ��̂ŁA�����̕ҏW�L�[�Ɠ����@�\���ʂ���forward�R�}���h�Abackward�R�}���h�̐ݒ肳��Ă���t�@���N�V�����E�L�[��T���Ċm�F���Ă������Ƃł���B
�@PC��SAS�ł́A(f�2)�L�[��keys�R�}���h���ݒ肳��Ă���̂ŁA�킴�킴Command�s�ɓ��͂��Ȃ��Ă��A(f�2)�L�[(=keys)�������悢�B�����ɁA(f�2)�L�[�������Ă݂āAKEYS�E�B���h�E���\�������̂��m�F���Ă݂悤�BKEYS�E�B���h�E����邽�߂ɂ́AKEYS�E�B���h�E��Command�s��
�@�@�@Command ===> END
�Ɠ��͂���悢�BHELP�E�B���h�E�ɂ��Ă����l�ɁAend�R�}���h�ɂ���ăE�B���h�E����邱�Ƃ��ł���̂ŁA(f�1)�L�[(=help)�������Ă݂āAHELP�E�B���h�E��\�������Ă݂Ă��玎���Ă݂悤�B
�@�J�[�\���E�L�[�ł���(��)(��)(��)(��)�ɂ���āA�J�[�\���̓f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉�ʏ���A�E�B���h�E�̋��E���ɊW�Ȃ����R�Ɉړ������邱�Ƃ��ł��邪�A(f�5)�L�[(=next)���������ƂŁA�E�B���h�E�Ԃ����ԂɃJ�[�\���ړ������邱�Ƃ��ł���B�܂��A(f�3)�L�[(=log)�A(f�4)�L�[(=output)�A(f�6)�L�[(=prg)�ɂ���āA�_�����E�B���h�E�ɁA�ꔭ�ŃJ�[�\�����ړ������邱�Ƃ��ł���̂ŁA�����Ă݂悤�B
�@�����Ƃ��A���ۂɂ́ASAS�v���O���������n�߂�Ƃ��́APROGRAM EDITOR�E�B���h�E�����g��Ȃ��̂ŁA(f�7)�L�[(=zoom)���g���āAPROGRAM EDITOR�E�B���h�E��������ʈ�t�ɕ\������Y�[�~���O���s���A�\���L���Ƃ���������Ƃ��₷���B����zoom�R�}���h�͕\2.1�ɂ�����悤�ɁAon/off���J��Ԃ��X�C�b�`�̂悤�ɋ@�\����̂ŁA�ʏ�̃}���`�E�E�B���h�E�E���[�h�̏�Ԃɖ߂��ɂ́A������x(f�7)�L�[(=zoom)�������悢�B
�@�e�E�B���h�E�̓��e�́ASAS�v���O�����ł��A�f�[�^�ł��A�o�͌��ʂł��A�����ă��O�ł��A����������l�ɁA��������炪���݂��Ă���e�E�B���h�E��Command�s��
�@�@�@Command ===> FILE '�t�@�C����'
�Ɠ��͂���A�t�@�C���ɕۑ����邱�Ƃ��ł���B����file�R�}���h���g�p����Ƃ��ɂ́A�t�@�C�����͕K���A'�@'�ň͂ނ悤�ɂ���B
�@PC��SAS�ł́AMS-DOS�̃t�@�C������
�@�@�@[�h���C�u��:][���p�X����]�t�@�C����[.�g���q]
�̂悤�Ɏw�肳���B�����Ńp�X���Ƃ́A���[�g�E�f�B���N�g������ړI�̃f�B���N�g���ɒB����܂ł̃f�B���N�g���̓���(�p�X)���������߂ɁA�e�f�B���N�g���������ŋ���ĕ��ׂĕ\�������̂ł���B�Ⴆ�A���̂悤�ɂł���B
�@�@�@Command ===> FILE '��MYDIR��JPCDATA.SAS'
�����Ƃ��A�J�����g�E�f�B���N�g����MYDIR�ł���A���̗�ɂ���悤�ȃp�X���͏ȗ����邱�Ƃ��ł��āA
�@�@�@Command ===> FILE 'JPCDATA.SAS'
�Ɠ��͂��������ł��A���l�Ƀf�B���N�g��MYDIR�̂��Ƃɕۑ������B����
�@�@�@Command ===> FILE 'B:JPCDATA.SAS'
�Ƃ���ƁA�����w�肷�邾���ŁA�h���C�uB�ɂȂ��Ă���t���b�s�B�E�f�B�X�N�ɂ��t�@�C�����ۑ��ł���̂ŁA�v���O������f�[�^�̕ۑ���ڐA�A�o�͂̕ۑ��Ȃǂɂ͔��ɕ֗��ł���B
�@MS-DOS�̃t�@�C�����̊g���q�͕K���t���Ȃ��Ă͂Ȃ�Ȃ��Ƃ������̂ł͂Ȃ����A�t�@�C���̓��e�̕��ނ̂��߂ɁA�M�҂�PROGRAM EDITOR�E�B���h�E����ۑ������v���O������f�[�^�ɂ�SAS�ALOG�E�B���h�E����ۑ��������O�ɂ�LOG�AOUTPUT�E�B���h�E����ۑ������o�͌��ʂɂ�LST�Ƃ����t�@�C�����g���q��t���邱�Ƃɂ��Ă���B�g���q���g�����Ƃ��A�Ⴆ��JPC�AJPC.SAS�AJPC.LOG�AJPC.LST�͂��ꂼ��܂������ʂ̃t�@�C�����Ӗ����邱�ƂɂȂ�B
�@CMS��SAS�ł��A�t�@�C�����̌`�����قȂ邾���ŁAPC��SAS�Ƃ܂��������l�ɁA�e�E�B���h�E�̓��e�́A����炪���݂��Ă���e�E�B���h�E��Command�s��file�R�}���h��CMS�̃t�@�C������
�@�@�@Command ===> FILE 'fn ft [fm]'
�Ɠ��͂���ACMS�t�@�C���ɕۑ����邱�Ƃ��ł���B�t�@�C���E���[�hfm�͏ȗ������A������l�ƂȂ��Ă���B
�@�������ɓ����t�@�C����fn ft��CMS�t�@�C�������݂��Ă���ꍇ�ɂ́A����file�R�}���h�̎��s�ɂƂ��Ȃ��A
�@�@�@WARNING: The file already exists. Enter R to replace it, enter A to append to it or enter C to cancel FILE command.
�ƕ����Ă���̂ŁACMS�t�@�C���̓��e���X�V����ꍇ�ɂ�R�A�t������ꍇ�ɂ�A�Afile�R�}���h�����~�߂�ꍇ�ɂ�C����͂��Ă���(���s)�L�[�������B
�@�Ƃ���ŁA���������v���O�����A���O�A�o�͓��e�́A�]���́u�펯�v���炷��ƁA�K�����̏�Ƀv�����g�E�A�E�g���A�n�[�h�E�R�s�[�Ƃ��ĂƂ��Ă������ƂɂȂ�B���ہAPC��SAS�ł́A�e�E�B���h�E��file�R�}���h��p���A���������t�@�C����'PRN'��MS-DOS�t�@�C���ɏo�͂���悤�ɁA
�@�@�@Command ===> FILE 'PRN'
�Ɠ��͂���ƃv�����^�ɏo�͂��A����ł��邱�ƂɂȂ��Ă���B(�������A����ɂ̓v�����^�̐ݒ肪�K�ɍs���Ă���K�v������̂ŁA���ӂ�v����B) �������A����̓��[�h�E�v���Z�b�T�[�̃p�\�R���E�\�t�g��[�v����p�@�����ꂾ�����y���������ɂ����ẮA�قƂ�Ǘp���̖��ʌ����ɂ����Ȃ��B���������o�͓��e�́A�����Ȃ莆�̏�Ɉ�������ɁAfile�R�}���h�ɂ���āAMS-DOS�t�@�C���Ƃ��ČŒ�f�B�X�N��t���b�s�B�E�f�B�X�N�ɏ����o���A���̏�ŁA����MS-DOS�t�@�C�����g�����ꂽ���[�h�E�v���Z�b�T�[�ɂ���ĕҏW���A�K�v�Ȃ��̂������������K��������ׂ��ł��낤�B
�@����MS-DOS�t�@�C����CMS�t�@�C���Ƃ��ĕۑ����Ă�����SAS�v���O������f�[�^�́APROGRAM EDITOR�E�B���h�E�Ɍ����Ă͓ǂݍ��ނ��Ƃ��ł���B���̏ꍇ�ɂ́AMS-DOS�t�@�C����CMS�t�@�C���ɕۑ����Ă�����SAS�v���O�����̃t�@�C������PROGRAM EDITOR�E�B���h�E��Command�s��
�@�@�@Command ===> INClude '�t�@�C����'
�Ɠ��͂��āA��ʏ�ɓǂݍ��߂悢�B�����Ƃ��A�ǂݍ�����Ƃ����Ă��A����MS-DOS�t�@�C����CMS�t�@�C����������킯�ł͂Ȃ��B����Ή�ʏ�ɃR�s�[���Ă���킯�ł���BSAS�v���O���������ł͂Ȃ��A������t�@�C�����ǂݍ��݉\�ł���B���������āASAS�v���O�����͂������f�[�^�̃t�@�C���̕ҏW�A�ύX��PROGRAM EDITOR�E�B���h�E���g����B����ɂ͑��̃t�@�C���̃G�f�B�^�[�Ƃ��Ďg�p���邱�Ƃ��\�ł���B������CMS��SAS�ł́A�f�[�^�̃t�@�C����ǂݍ��ނƂ��ɂ́A
�@�@�@WARNING: The file contains sequence numbers. Enter R to remove the sequence numbers or K to keep the sequence numbers.
�ƕ����Ă���̂ŁAK�Ɠ��͂��Ă���(���s)�L�[�������B
�@�Ƃ���ŁAPC��SAS�ł��ACMS��SAS�ł��A����PROGRAM EDITOR�E�B���h�E��ʂɃv���O�����A�f�[�^���̓��e���\������Ă���ꍇ�ɂ́A���̓��e�̍Ō㕔�ɑ����ăt�@�C����ǂݍ��ނ��ƂɂȂ�BPROGRAM EDITOR�E�B���h�E�ɕ\������Ă�����e���������ꂽ��ŁA�S�ʓI�ɐV���ȃt�@�C���ɒu���������čX�V����邱�Ƃɂ͂Ȃ�Ȃ��̂Œ��ӂ��K�v�ł���B�t�@�C�����e�̑S�ʓI�X�V���������Ƃ��ɂ́A��q����clear�R�}���h���g���āA��U�APROGRAM EDITOR�E�B���h�E�̓��e���������Ă����K�v������B
�@�V�K��SAS�v���O�������쐬����ꍇ�ɂ́APROGRAM EDITOR�E�B���h�E�̒��̍s�ԍ��̂��Ă���s�Ȃ�A�ǂ�����ł����R�ɕ�������������ł����悢�B�J�[�\���E�L�[���g��Ȃ��Ă��A���^�[���E�L�[(��)���g���A���s���邱�Ƃ��o����B�������A�s�ԍ��̎���1�����͕ی�t�B�[���h�ƌĂ�A��������͂��悤�Ƃ���Ɓu�s�b�v�ƌx���������āA���͎͂t�����Ȃ��̂Œ��ӂ�����B
�@PROGRAM EDITOR�E�B���h�E�ɕ\������Ă���ŏI�s�܂Ŏg�������ꍇ�ł��A���^�[���E�L�[(��)��������1�s��ɃX�N���[�����āA�V����1�s�\�������̂œ��͂���������B(ROLL DOWN)�L�[�������āA��C�Ɏ��̉�ʂɐi�ނ��Ƃ��ł���B�O�̍s�������蒼�����肵�����Ƃ��ɂ́A(ROLL UP)�L�[�������āA�O�̉�ʂɖ߂��悢�BCMS��SAS�ł́A (ROLL DOWN)�L�[�A(ROLL UP)�L�[���g���Ȃ��̂ŁA�����̃L�[�̑���ɁAforward�R�}���h�Abackward�R�}���h�̐ݒ肳��Ă���t�@���N�V�����E�L�[��p����B
�@SAS��PROGRAM EDITOR�E�B���h�E�̕ҏW�@�\���i��G�f�B�^�[�̓t���E�X�N���[���E�G�f�B�^�[�ƌĂ�A�������܂ꂽ��������ʂ̃C���[�W�ʂ��SAS�v���O�����Ƃ��Ĉ����邱�ƂɂȂ�B(���Ȃ݂ɁA���ꂪ���Ƀt���E�X�N���[���E�G�f�B�^�[�ł͂Ȃ��A���C���E�G�f�B�^�[�ł���A���͂��ύX���������s�́A�R�}���h���͂̂悤�ɁA�e�s�Ń��^�[���E�L�[(��)�������āA�v�Z�@�ɂ��̎|���m�F���Ȃ��Ƃ����Ȃ��B��ʏ�̕ύX�͂����܂ʼn�ʏ�ł݂̂̕ω����Ӗ����A�z�X�g�v�Z�@�̋L�����u��̕ω����Ӗ����Ȃ��̂ŁA�ҏW�͏�ɍs�P�ʂōs��Ȃ���Ȃ�Ȃ��̂ł���B���̓_�A�t���E�X�N���[���E�G�f�B�^�[�͔��ɕ֗��ł���B)
�@PROGRAM EDITOR�E�B���h�E�ł͎��̂悤��SAS�ҏW�R�}���h���g�p�ł���B
�@SAS�ҏW�R�}���h�̂����ł��A�X�N���[���E�R�}���h�̓R�}���h�s�ɓ��͂��Ďg�p����R�}���h�ł���B�����ŁA�X�N���[���E�R�}���h���g�p����ۂɂ̓J�[�\���E�L�[�Ȃǂ��g���āA�J�[�\�����R�}���h�s�Ɉړ������Ă���R�}���h�̓��͂��s���B���邢��PC��SAS�ł́A��̃L�[����
�@�@�@(SHIFT)+(HOME CLR)
�Ɖ����A�ꔭ�ŃJ�[�\�����R�}���h�s�Ɉړ������邱�Ƃ��ł���̂ŕ֗��ł���BCMS��SAS�ł́A����Ɠ����@�\������home�R�}���h��ݒ肵���t�@���N�V�����E�L�[�����ʂ͂���͂��Ȃ̂ŁA�����KEYS�E�B���h�E�ŒT���Ďg���悢�B
�@�t�@���N�V�����E�L�[�Őݒ肳��Ă���R�}���h�����Ƃ��Ƃ̓X�N���[���E�R�}���h�Ȃ̂ŁA�Ⴆ�AHELP�E�B���h�E��\��������ۂɂ́APC��SAS�ł�(f�1)�L�[�������Ă��������A�R�}���h�s��
�@�@�@Command ===> HELP
�Ɠ��͂��Ă������B�@�\�Ƃ��Ă͓������ƂɂȂ�B�t�@���N�V�����E�L�[�Őݒ肳��Ă��Ȃ��X�N���[���E�R�}���h�����邪�A�悭�g�����̂Ƃ��ẮA�Ⴆ�Ύ��̂悤�Ȃ��̂�����B
�@SAS�ҏW�R�}���h�̂����ł��s�R�}���h�ƌĂ��R�}���h�Q�́A����܂ł̃X�N���[���E�R�}���h�Ƃ͈قȂ����g����������B�s�R�}���h�́A�ҏW��ʍ��[�ɕ���ł���5���̍s�ԍ�����(�����=====�Ŏ������Ƃɂ��悤)�ɁA�s�ԍ��̏��(1���ڂ���̕K�v�͂Ȃ�)�d�ˏ�������`�œ��͂��āA���^�[���E�L�[(��)�������A�g�p����R�}���h�ł���B���̂悤�ȃR�}���h�����p�\�ł���B



�@SAS�v���O�������ł�����A(f�10)�L�[(=zoom off; submit)�������āAPROGRAM EDITOR�E�B���h�E��̃v���O������SAS�ɒ�o��(submit)�A���s�����Ă݂�B�������A�������ُ�I�����邱�Ƃ�����̂ŁAsubmit����O��SAS�v���O������MS-DOS�t�@�C���ɕۑ����Ă����Ȃ��ƁASAS�v���O�����͎����Ă��܂����Ƃ�����Bsubmit�̑O�ɂ��܂߂�file���Ă����������S�ł���B
�@���܂�SAS�v���O�����̎��s�ɐ�������ƁA�o�͂������OUTPUT�E�B���h�E�ɕ\������邱�ƂɂȂ�BCMS��SAS�ł́A���܂�SAS�v���O�����̎��s�ɐ������āA�o�͂�����A���̒i�K�ŁA�f�B�X�v���C��ʑS�ʂ�OUTPUT�E�B���h�E�ɐ�ւ��B
�@������ɂ���ASAS�v���O�����̎��s�����s���A���܂������Ȃ������ꍇ�ɂ́ALOG�E�B���h�E��ɓW�J���ꂽ���s���ʂ��������A���܂������Ȃ������������`�F�b�N����K�v������B���܂����s����Ȃ����������́A�قƂ�ǂ��v���O�����̕��@��̌���R�}���h�̒Ԃ蓙�̌��ŁA�����̓G���[�Ƃ��āALOG�E�B���h�E�ɕ\�������B���������v���O������̃G���[�̓o�O(bug����)�ƌĂ�A�G���[���炯�Œ��H����Ԃ̃v���O�����͓����Ȃ��BLOG�E�B���h�E�ɕ\������Ă��郁�b�Z�[�W�𒍈Ӑ[���������āA�G���[����菜���A�v���O�������C�����Ď��s�\�ȃv���O�����Ɏd�グ�邱�Ƃ𒎂���菜���Ƃ����Ӗ��Ńf�o�b�O(debug)�Ƃ����B
�@���S�҂��悭�����ŁA�������{�l���Ȃ��Ȃ��C�����Ȃ����́A���̂悤�Ȍ����ڂɂ͎��Ă��镶���A�L���̑ł��ԈႢ�ł���B
�@�f�o�b�O���邽�߂ɂ́A�܂����s�Ɏ��s����SAS�v���O�������Ăі߂��Ȃ���Ȃ�Ȃ��B�����ŁA(f�9)�L�[(��recall)�������āA���O�Ɏ��s�����v���O������PROGRAM EDITOR�E�B���h�E��ɌĂі߂��Ă���B�����ŁA���̌Ăі߂���Ă����v���O�����̏C�����s���A�ł�����܂����s�����Ă݂�B�����Z���v���O�����������āA�v���O��������x�Ő���Ɏ��s����邱�Ƃ͂߂����ɂȂ��B�ʏ�͉��x�����s�A�C���̃T�C�N�����J��Ԃ��āA�悤�₭�܂Ƃ��ɓ����v���O�������ł�����̂ł���B���ꂾ���ɁA�����őg�v���O���������ۂɓ������Ƃ��ɂ́A����Ȃ�̊�����������̂ł���B���̊����𖡂키���߂ɂ��A�����ł��������ɁA���܂߂Ƀf�o�b�O���邵���Ȃ��̂ł���B
�@PROGRAM EDITOR�E�B���h�E���SAS�v���O�����́A���̂܂�SAS���I�����Ă��܂��Ǝ����Ă��܂��B�����ŁA��������SAS�v���O�����́A�t�@�C���Ƃ��ĕۑ����Ă������B�l�Ԃ̎��ƂƂ͈Ⴂ�A�v���O�����ƃf�[�^�����ۑ����Ă����A�ǂ�Ȃɒ����o�͌��ʂł����Ă��A�R���s���[�^�̏����ɂ�100%�̍Č���������BSAS�v���O�������t�@�C���Ƃ��ĕۑ����邽�߂ɂ́A���ɁA(3)�ł��q�ׂ��悤�ɁA
�@�@�@Command ===> FILE '�t�@�C����'
�Ɠ��͂���B�������邱�ƂŁAPROGRAM EDITOR�E�B���h�E��ɂ���SAS�v���O�������APC��SAS�ł͎w��t�@�C������MS-DOS�t�@�C���ɁACMS��SAS�ł͎w��t�@�C������CMS�t�@�C���ɂ��ꂼ�ꏑ���o����A�ۑ������B�܂��ɁA�t�@�C�������̂ł���B
�@�ȏ�̂悤�ȍ�Ƃ��s���āASAS���I������ۂɂ́A
�@�@�@Command ===> BYE
�Ɠ��͂���悢�B�������A����SAS�I���ɂ���āAPROGRAM EDITOR�E�B���h�E��SAS�v���O�����������邾���ł͂Ȃ��ALOG�E�B���h�E�AOUTPUT�E�B���h�E�̓��e��������B���́ALOG�E�B���h�E�AOUTPUT�E�B���h�E�̓��e�́A�r��clear�R�}���h�����s���Ȃ�����ASAS���N�����Ă���I������܂�(������Z�b�V�����ƌĂ�)�̊ԁA�����邱�ƂȂ��~�ρA�ۑ�����Ă���̂ł���B���������āA��ʂ��X�N���[�������邱�ƂŁA���̃Z�b�V�����ł���܂łɎ��s����Ă��������ʂ��Q�Ƃ��邱�Ƃ��\�ł���B���̂��Ƃ����邽�߂ɁA�Z�b�V���������܂蒷�������āA�v���O�����𗬂������Ă���ƁA�L���A�~�ς����e�E�B���h�E�̓��e���c��ɂȂ肷���āA�v���O�������s�̍ۂُ̈�I���̌����Ƃ��Ȃ�̂ŁA�Ƃ��ǂ��̓E�B���h�E�̓��e��clear���邩�A���邢�͂������̂��Ǝ��XSAS�Z�b�V�������I�������������悢�B
�@���̂悤�ɁAbye�R�}���h�ɂ���āALOG�E�B���h�E�AOUTPUT�E�B���h�E�̓��e�������邪�A���ɏq�ׂ��悤�ɁA���ꂼ��̃E�B���h�E��file�R�}���h���g���AMS-DOS�t�@�C�����邢��CMS�t�@�C���Ƃ��ĕۑ����邱�Ƃ͉\�Ȃ̂ŁA�K�v�Ȃ��������Ƃ悢�B
�@SAS�v���O�����́ASAS���ƌĂ�镶�ɂ���č\���������̕��͂ł���BSAS����SAS�V�X�e���ɑ��Ă��鏈���������邽�߂̖��ߕ�������ASAS�V�X�e�����ǂ�ŗ����ł���悤�Ȍ`���A���@�ŏ����ꂽ���̂łȂ��Ă͈Ӗ����Ȃ��B�eSAS���͌`���I�ɂ� ";" (�Z�~�R����)�ŏI�����܂߂�������ł��邪�A
�@�������A"*" �Ŏn�܂�SAS���̓R�����g�Ƃ݂Ȃ���ASAS�V�X�e���͓ǂݔ�����ƂɂȂ��Ă���B�܂�A"*" �Ŏn�܂�R�����g���́ASAS�V�X�e���̂��߂ɂł͂Ȃ��A�v���O�����쐬�Ҏ��g���܂߂��l�Ԃ̂��߂ɏ��������̂ł���B���ہA�N�����l�̂��߂Ƃ��������A�����̎������v���O�����̓��e�𗝉��ł���悤�ɂ��邽�߂ɁA�v���O�����̉�����R�����g�̌`�œ���Ă����������悢�B
�@SAS�́A���p�҂��쐬�����f�[�^�E�Z�b�g�ɑ��āA���p�҂��w�肵�A�Ăяo�����e�퓝�v�p�v���O����(SAS�ł͂��̂悤�ɂ��炩���ߗp�ӂ��ꂽ���ꂼ��̃v���O�������v���V�W��(procedure)�ƌĂ�ł���)���@�\�I�Ɍ��ѕt���邽�߂̃V�X�e���ł���B���p�҂�SAS�ɑ��āA�f�[�^�E�Z�b�g�̍쐬�Ɗ�]����v���V�W���̎w�肳���s���悭�A���Ƃ�SAS�����v�������s���Ă����̂ł���B���������āASAS�v���O�����́A��{�I�ɂ͎��̂Q��ނ̃X�e�b�v�̌J��Ԃ��Ƃ��č\�������B
�@DATA�X�e�b�v�ō쐬�E���H�̑ΏۂƂȂ�APROC�X�e�b�v�œ��v�����̑ΏۂƂȂ�SAS�f�[�^�E�Z�b�g�́A����Ȍ`���̃t�@�C���ł���B����̓I�ɁA����[�����������ꍇ��z�肷��Ƃ킩��₷�����A�����Ώۂł���e�l�A�����SAS�ł̓I�u�U�[�x�[�V���� (observation)�ƌĂ�ł��邪�A���̃I�u�U�[�ׁ[�V�������ƂɁA�e����ɑ����\�`���ɂ܂Ƃ߂Đ����������̂ƂȂ��Ă���BSAS���ɂ����ASAS�f�[�^�E�Z�b�g�̓I�u�U�[�x�[�V�����ԍ�1, 2, 3,...���ƂɁA�������̕ϐ�(variable)�A�Ⴆ��X1, X2, X3,...�ɑ���f�[�^�l���������\2.3�̂悤�ȕ\�`���̃t�@�C���Ƃ������ƂɂȂ�B����Ε\�`���̃f�[�^�E�x�[�X�ł���B
�\2.3�@SAS�f�[�^�E�Z�b�g�̍\��
| �I�u�U�[�x�[ �V�����ԍ� | �ϐ� | |||
|---|---|---|---|---|
| X1 | X2 | X3 | �@�������@ | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| : : | ||||
�@SAS�f�[�^�E�Z�b�g�ɂ́A
�@SAS�f�[�^�E�Z�b�g�͌��̃f�[�^�E�t�@�C���ɔ�ׂ�Ƃ��Ȃ�傫�ȗe�ʂ�K�v�Ƃ���BPC��SAS�ł́A���̏͂Ō�q�����{�^�v���O�����ł�82.5KB���x�̃f�[�^�E�t�@�C������607.5KB���x��SAS�f�[�^�E�Z�b�g����������A7.4�{�ɂ��Ȃ�B�ʏ�͂����Ƒ��푽�l�ȕϐ����쐬�����̂ŁA�Ⴆ�A���̏͂̒ʏ�^�v���O�����ł́A�����f�[�^�E�t�@�C������1.2MB���x��SAS�f�[�^�E�Z�b�g�����������B����14.5�{�ł���B�ꎞSAS�f�[�^�E�Z�b�g�ł��ASAS�I�����܂ŏ�������Ȃ��̂ŁA1���SAS�Z�b�V�����̊ԂɁA�قȂ閼�O�̈ꎞSAS�f�[�^�E�Z�b�g������������ƁA��e�ʂ̌Œ�f�B�X�N�ł��A�����Ƃ����Ԃɋ̈���g���s�������ƂɂȂ�̂ŁA���ɁA�p�[�\�i���E�R���s���[�^��SAS���g���ꍇ�ɂ́A�ł��邾���������O��SAS�f�[�^�E�Z�b�g���J��Ԃ��J��Ԃ��g�p���������A�f�B�X�N�e�ʂ̐ߖ�ɂȂ�B�܂��ASAS�f�[�^�E�Z�b�g�̐����ɂ́A���̓s�x���Ԃ�������̂ŁA���C���t���[���Ȃ�Ƃ������A�p�[�\�i���E�R���s���[�^�ł͓����ꎞSAS�f�[�^�E�Z�b�g�����x����������͎̂��Ԃ̖��ʂł���B���̂��߁A�{���ł́A��x�A�i�vSAS�f�[�^�E�Z�b�g�����Ă����A��̃v���O�����͂�����J��Ԃ��ė��p���邱�Ƃ������Ƃ��Ă���B
�@SAS�ł͕ϐ����͉p���Ŏn�܂�8�����ȓ��̉p�����Ƃ��邱�ƂɂȂ��Ă���B�ő�4,000�܂ŕϐ����`���邱�Ƃ��\�ł���B�܂��A�ϐ��ɂ͐��l�f�[�^�������f�[�^���^���邱�Ƃ��ł���B�������A�ϐ��ɕ����f�[�^��^����ۂɂ́A���ꂪ�����f�[�^�ł��邱�Ƃ�����K�v������B��̓I�ɂ́A�����f�[�^�� '�@' �ň͂ނ��ƂŁA�Ⴆ��
�@�@�@'123'�@'ABC'�@'ASA100'
�̂悤�ɁA���ꂪ�����f�[�^�ł��邱�Ƃ�����B���������āA123�͕S��\�O�Ƃ����u���l�v�ł��邪�A'123' ��123�Ƃ����u�����v�܂蕶����ł��邱�Ƃ��Ӗ����Ă���B�ϐ��̂Ƃ肤��l�́A���l�f�[�^�̏ꍇ�ɂ� �}10-73�`1073 �͈̔́A�����f�[�^�̏ꍇ�ɂ� 1�`200����(�o�C�g)�ł���B
�@����[�����̏ꍇ���l����Ƃ킩��悤�ɁA���������ۂɍs���ƁA�ꕔ���̎���[�Ƃ����̂��A������x�̊����ŏo�Ă��邱�ƂɂȂ�B�܂�A�I�u�U�[�ׁ[�V�����ɂ���ẮA���ۂɂ͒l�̑��݂��Ȃ��ϐ������������݂��邱�ƂɂȂ�B���������ꍇ�ɂ́ASAS�V�X�e���ɕϐ��̒l���u�������Ă���v�Ƃ������ƒm�点�邽�߂ɁA�f�[�^�E�G���g���[���s���ۂɁA���炩�́u�l�v��^���Ȃ��Ă͂Ȃ�Ȃ��B���́u�l�v�̂��Ƃ������l�ƌĂсASAS�ł͕ϐ��ɕ\2.4�̌����l��^���Ă����ƁASAS�����v�������s�Ȃ��ۂɁA�����Ώۂ̕ϐ��������l�ł���I�u�U�[�ׁ[�V�����ɂ��ẮA���炩���߂������������Ŋe�폈�����s���邱�ƂɂȂ��Ă���B
�\2.4�@�����l
| ���l�ϐ� | �����ϐ� | |
|---|---|---|
| �����l�������f�[�^ |
|
|
| ���Ɍ����l�Ƃ��Ĉ�������̓f�[�^ |
|
|
�@�܂��ASAS�v���O�����̒��ł͕ϐ��������X�g��ɕ��ׂėp������A�����悤�ȕϐ��������������肷��悤�ȃP�[�X���N����B���́A���̕����v���O�����������ۂɂ͊y�Ȃ̂ł���B�Ȃ��Ȃ�A�Ⴆ�A�܂̕ϐ�����ׂ�
�@�@�@X1 X2 X3 X4 X5
�̂悤�ȏꍇ�ɂ́A
�@�@�@X1-X5
�Ƃ����ȗ��`���g���邩��ŁA����͂ƂĂ��֗��ł���B��ʓI�ɂ́AXm-Xn �ƋL���ƁAXm����Xn�܂ł̂��ׂĂ̕ϐ�(m<n)��\�����ƂɂȂ�B���l�ɁAX--Z �ƋL���ƁASAS�v���O��������X����Z�܂ł̊Ԃɒ�`���ꂽ���ׂĂ̕ϐ���\�����ƂɂȂ�B���̂ق��ɂ��A
�@�@�@_ALL_ �c�c���ׂĂ̕ϐ�
�@�@�@_NUMERIC_ �c�c���ׂĂ̐��l�ϐ�
�@�@�@_CHARACTER_�c�c���ׂĂ̕����ϐ�
�̂悤�ȏȗ��`���p�ӂ���Ă���B
�@�Ƃ���ŁA�ϐ������l���o���Ƃ����̂́A�ӊO�Ƒ�ςȍ�Ƃł���B�ϐ��̐���������قǂ��̑�ς��͐g�ɐ��݂Ă���B���ہA�ϐ������l�����{�l�ł���A�ϐ��������������ł́A���̕ϐ����ǂ̎��⍀�ڂɑΉ����Ă����̂����킩��Ȃ��Ȃ��Ă��܂��B�������A�ϐ��������G�ō������Ă������قǁA�����قǂ̂悤�ȕϐ����̏ȗ��`���g���ɂ����Ȃ��Ă���̂ł���B�����ŁA�����߂Ȃ̂́A�M�҂����s���Ă��邿����Ƃ����H�v�ł���B��6���ł��G��邪�A�܂��A�ϐ������X�g�̏ȗ��`���g���₷���悤�ɁA�ϐ����̖����͐���������̏��ɕt�������̂��悢�B�܂��ϐ����͉p������n�߂Ȃ��Ă͂����Ȃ��B���������āA����[�̐v�i�K�ŁA���O�Ɏ���ԍ���
�@�@�@�A���t�@�x�b�g�܂��̓��[�}�����ɂ��啪�ށm�{�����ށn�{�����ɂ�鏬����
�Ƃ����\���ɂ��Ă����̂ł���B�Ⴆ�A
�@�@�@����ԍ��@�@II.3�@�@IV.4�@�@A.III.5�@�@D.IX.9
�@�@�@�ϐ����@�@�@II3 �@�@IV4 �@�@AIII5 �@�@DIX9
�Ƃ����悤�ɂ���ƁA�ȒP�ɕϐ������t�����邵�A�t�ɕϐ���������A���̎���ԍ��������ɂ킩��̂ł���BSAS�v���O�����ŕϐ������`����Ƃ��Ɏ���[�̎���ԍ������̂܂ܕϐ����ɂ��邱�Ƃ��ł��āA�֗��ŊԈႢ�����Ȃ��B�������A�ϐ�����8�����ȓ��Ȃ̂ŁA����ԍ������߂�Ƃ��ɂ͂Ȃ�ׂ��V���v���ɂ��������悢���Ƃɕς��͂Ȃ����c�c�B�ϐ��̋�̓I�ȈӖ����e�ɂ��ẮA�ϐ����ɔ��f������̂ł͂Ȃ��A��q����悤�ȕϐ����x����p���������悢�B����ŏo�͎��ɕ\�����邱�Ƃ��ł��A���̍ۂɂ͎���������40�����ȓ��Ƒ啝�Ɋɂ��Ȃ��Ă���A���{��A�����Ȃǂ��g���A�͂邩�Ɏ��p�I�ł���B
�@���̐߂ł́A���ۂɊȒP��SAS�v���O�������쐬���A�f�[�^�E�G���g���[�ƒP���W�v�y�щi�vSAS�f�[�^�E�Z�b�g�̐������s���Ă݂悤�B���̈�A�̃v���Z�X��SAS�v���O�����̊�{�𗝉����Ă��炤���߂ɁA���̐߂ł́A�����Ƃ��V���v���Ȋ�{�^SAS�v���O���������グ��B���̊�{�^�v���O������i��������`�ŁA���̐߂ŁA�M�҂����ۂɒ����̂Ƃ��Ɏg�p����ʏ�^SAS�v���O�����ւƔ��W������B�����Ƃ��A��{�^�v���O�����ł��~���o���˂A�\�����p�ɂȂ�B
�@�Ⴆ�A��6���Œ����̎���Ƃ��Ă�����u�g�D�������̂��߂̏]�ƈ��ӎ������v�œ���ꂽ�́A�����[�̂܂܂ł́A�l�Ԃɂ͓ǂ߂Ă��A�R���s���[�^��SAS�͓ǂݎ�邱�Ƃ��ł��Ȃ��B�����ł܂��ŏ��ɁA�R���s���[�^��SAS���ǂݎ��\�Ȍ`�̃f�[�^�ɏ��������Ă��K�v������B��̓I�ɂ́A���f�[�^�l�Ƃ��āA����K���ɑ����ăf�B�X�v���C��ʏ��t�@�C����ɏ������ׂĂ��̂ł���B������f�[�^�E�G���g���[�Ƃ����B�悭�p�������\�I�ȃf�[�^�l�̏������ו��ɂ͎��̓�̌`��������B
���ꂼ��ɑΉ�����`�ŁA��q����INPUT���̕ϐ����̕��т̌`��������B�����̌`�����悭�g������͂̎d���ɂ��āA���ꂼ���̓I�ɐ������Ă������B
�@�����SAS�v���O���������ɒ��ڃf�[�^���������ޕ��@�ł���B���X�g�`���ł́A���X�g���͂��s���A�ϐ����̕��тɑΉ������Ȃ���f�[�^�l��ǂݍ��ށB��ʓI�ɂ́A�ϐ����̕��т́AINPUT����
�@�@�@INPUT �ϐ���1 �ϐ���2�@�c�c;
�Ƃ��̂܂ܕϐ������������ׂ�`�����Ƃ�B���X�g���͂̏ꍇ�A�f�[�^�l�͋ɂ���ċ����Ƃ������Ƃ̑��ɁA
�Ȃǂɒ��ӂ��Ȃ��Ă͂Ȃ�Ȃ��B
�@���܁A���̕����Ńf�[�^����͂��A�i�vSAS�f�[�^�E�Z�b�g�����邱�Ƃ��l���悤�BPC��SAS�ł́A���̂悤�ɂ���B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; DATA libname.�i�vSAS�f�[�^�E�Z�b�g���{��; INPUT �ϐ����̕���; CARDS; �@�@�@�@�@�@�@�@�f�[�^�s ; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; DATA SAVE.JPC; INPUT KC SC IC I1-I4; CARDS; 5 7 01 1 8 1 4 5 7 02 1 3 1 4 5 7 03 1 3 1 3 5 7 04 1 3 1 4 5 7 05 1 5 1 2 5 7 06 1 5 2 3 5 7 07 1 3 1 2 5 7 08 1 5 1 2 ; |
�@PC��SAS�ł́A�i�vSAS�f�[�^�E�Z�b�g�̃t�@�C�����̊g���q�͕K�� "SSD" �Ƃ��Đ��������B���̃v���O������̏ꍇ�ɂ́A"JPC.SSD" �Ƃ����t�@�C�����̉i�vSAS�f�[�^�E�Z�b�g��MS-DOS�t�@�C���Ƃ��Đ�������邱�ƂɂȂ�BLIBNAME���ł́A���̉i�vSAS�f�[�^�E�Z�b�g���ǂ��̃f�B���N�g���̉��ɐ��������̂����������߂̃p�X�����w�肳���BLIBNAME���ł��̃p�X���ƑΉ��Â���ꂽlibname (���C�u�����Q�Ɩ�)���A�p�X���̑���ɁA����SAS�Z�b�V�����̊ԁA�p�����邱�ƂɂȂ�B
�@���̃v���O������̏ꍇ�ł́AMYDIR �Ƃ����p�X���� "SAVE" �Ƃ���libname�Ɍ��ѕt���Ē�`���Ă���B���̎w��ɂ��A�i�vSAS�f�[�^�E�Z�b�gJPC.SSD�̓f�B���N�g��MYDIR�̉��ɐ�������邱�ƂɂȂ�ƂƂ��ɁA"SAVE.JPC" �� "��MYDIR��JPC.SSD" ���Ӗ����邱�ƂɂȂ�B
�@CMS��SAS�ł́APC��SAS�̂悤��libname�̎w�肪����Ȃ��B���ɁA��4��(2)(b)�ŏq�ׂ��悤�ɁACMS��SAS�ł́A�i�vSAS�f�[�^�E�Z�b�g����ft.fn ��ft����ɂ��邪�A����2���x�����̎w�肾���Ŏ����I�ɉi�vSAS�f�[�^�E�Z�b�g����������Alibname�͕K�v���Ȃ��B���������āACMS��SAS�ł�PC��SAS�ł͕K�v������1�s�ڂ�LIBNAME���͂����A2�s�ڂ�DATA������n�߂�B���̍ہA�`�̏�ł�PC��SAS��DATA������libname���w�肵�Ă����Ƃ���ŁACMS��SAS�ł͉i�vSAS�f�[�^�E�Z�b�g����ft���w�肷�邱�ƂɂȂ�(ft��WORK�ɂ���ƁA�ꎞSAS�f�[�^�E�Z�b�g�Ƃ��ĔF������Ă��܂��̂ŁA����ȊO�̂��̂ɂ��邱��)�BCMS��SAS�ł́A���̂悤�Ɏw�肷�邾���ŁCSAS�f�[�^�E�Z�b�g�͉i�vSAS�f�[�^�E�Z�b�g�ƂȂ�ADATA�X�e�b�v�ōs�������H�����́A���̂܂�CMS�t�@�C���Ƃ��ĕۊǂ���邱�ƂɂȂ�B���������āA�`���I�ɂ́APC��SAS�̃v���O������̂P�s�ڂ��폜�������̂��A���̂܂�CMS��SAS�̃v���O������ƂȂ�B���Ȃ킿�A
| CMS��SAS |
|---|
|
DATA �i�vSAS�f�[�^�E�Z�b�g��;�@�@�@�@�@ INPUT �ϐ����̕���; CARDS; �@�@�@�@�@�@�@�@�f�[�^�s ; |
| ��) |
|---|
|
DATA SAVE.JPC; INPUT KC SC IC I1-I4; CARDS; 5 7 01 1 8 1 4 5 7 02 1 3 1 4 5 7 03 1 3 1 3 5 7 04 1 3 1 4 5 7 05 1 5 1 2 5 7 06 1 5 2 3 5 7 07 1 3 1 2 5 7 08 1 5 1 2 ; |
�@������ɂ���A���X�g�`���̓f�[�^�l���ɂ���ċ���Ă����̂ŁA�ϐ��������Ȃ�ƁA���炯�ɂȂ�B�������A���܂�1�����ł���A�L�[��1�^�b�`��v����B���������āA�f�[�^���ʂɃG���g���[����ꍇ�ɂ́A������t�@�C���e�ʂ̓_�ł͖�肪���邱�Ƃɂ͒��ӂ�����B�܂��ASAS�v���O�������ɒ��ځA�f�[�^����������ł������ƂŁA��ʂ̃f�[�^�A�Ⴆ��1,000�I�u�U�[�ׁ[�V�����̃f�[�^�������ƁA�v���O�����̒������A�Œ�ł�1,000�s���邱�ƂɂȂ�A�f�[�^�̕ҏW�A�f�o�b�O�����l����Ǝ��p�I�ł͂Ȃ��B�����ōl������̂��A�v���O�����ƃf�[�^���t�@�C���Ƃ��ĕ������Ă������̂悤�ȕ����ł���B
�@�t�H�[�}�b�g�`���ł́A���X�g�`���̂悤�ɁA�f�[�^�l�̊Ԃɋ̋�肪�Ȃ��̂ŁA�f�[�^�E�t�@�C�������������ł́A�ǂ�����ǂ��܂ł���̃f�[�^�l�ɂȂ��Ă���̂����킩��Ȃ��B�����ŁA�f�[�^�E�t�@�C�����쐬�����l�Ԃ̑��ŁA���̃f�[�^�E�t�@�C���̒��Ńf�[�^�l���ǂ̂悤�ȏ����ŕ��ׂ��Ă���̂����w�����Ă��K�v������B
�@���܁AMS-DOS�t�@�C��JPCDATA.SAS�A���邢��CMS�t�@�C��JPCDATA SAS����f�[�^��ǂݍ��ނ��Ƃ��l���悤�B���̃t�@�C���ɂ́A(a)�̃v���O������Ɠ����f�[�^���}2.6�̂悤�ɓ����Ă���Ƃ���B�܂�A�ϐ�KC, SC, IC, I1, I2, I3, I4�ɑΉ�����f�[�^8�l�����A�}2.6�̂悤�ɕϐ��ɑΉ������Ȃ�����͂��Ă���B
�}2.6�@�f�[�^�E�t�@�C��(JPCDATA.SAS���邢��JPCDATA SAS)�̒��̃f�[�^�ƕϐ��̑Ή�
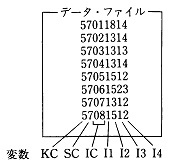
�@���͂����l�Ԃ̑��ł́A�}2.6�Ŏ������悤�ȑΉ������Ȃ�����͂����킯�ł��邩��A���̑Ή��W�̂��Ƃ�SAS���ɋ����Ă��Ȃ���Ȃ�Ȃ��B���̂Ƃ��A�e�ϐ��ɑΉ�����J�������w�肷�邽�߂ɗp������̂������ł���A���̏ꍇ�ɂ́A�Ⴆ�ΒP���ɕϐ��ƃJ�����̑Ή���t���āA
�@�@�@INPUT KC 1. SC 1. IC 2. I1 1. I2 1. I3 1. I4 1.;
���邢�́A�ϐ����̕��тƁA�����̂܂Ƃ܂���l���āA
�@�@�@INPUT (KC SC IC I1-I4)(2*1. 2. 4*1.);
�Ƃ����悤�Ɏw�肵�Ă��悢�B�܂�A���X�g�`���̂悤�ɁA�f�[�^�l�̊ԂɁA�̋�肪�Ȃ��̂ŁA�����̏�ŋ������Ă�낤�Ƃ����̂ł���B��ʓI�ɂ́AINPUT����
�@�@�@INPUT (�ϐ���1 �ϐ���2 �c�c)(�Ή����鏑��)[(�ϐ���3 �c�c)(�Ή����鏑��)�c�c];
�Ƃ����`�����Ƃ�B�������S�̂������āA�t�H�[�}�b�g�`���ł́u�ϐ����̕��сv�ƌĂԁB�܂�A�t�H�[�}�b�g�`���ł́u�ϐ����̕��сv�ɂ͏����܂Ŋ܂܂�Ă��邱�ƂɂȂ�B�����ŁA�����Ƃ͎��̂��̂��ŋ���ĕ��ׂ����̂������B
�@�@�@w.�@ �c�c�t�B�[���h�̒���w(1��w��32)�̐��l�f�[�^��ϐ��ɗ^����Ƃ�
�@�@�@$w. �@�c�c�t�B�[���h�̒���w(1��w��32)�̕����f�[�^��ϐ��ɗ^����Ƃ�
�@�@�@m*w.�@�c�c����w�̐��l�f�[�^�̃t�B�[���h��m����ł���ꍇ
�@�@�@m*$w. �c�c����w�̕����f�[�^�̃t�B�[���h��m����ł���ꍇ
�@�@�@+n�@�@�c�cn�J�����ǂݔ���Ƃ�
�܂��A��̃I�u�U�[�x�[�V�����ɑ���f�[�^��2�s�ȏ�ɂ킽��Ƃ��ɂ́A�ϐ����Ƃ���ɑΉ����鏑����2�s���ȏ�ɂ킽��Ȃ��悤�ɂ܂Ƃ߂ĕ����A���̊Ԃɍs�̋����������߂� "/" ������B
�@PC��SAS�ł́A���̂悤�ȏ�����p���āA�}2.6��MS-DOS�t�@�C��JPCDATA.SAS����̃f�[�^��ǂݍ��݁A�i�vSAS�f�[�^�E�Z�b�g������v���O�����͎��̂悤�ɂȂ�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; DATA libname.�i�vSAS�f�[�^�E�Z�b�g���{��; INFILE �f�[�^�E�t�@�C����; INPUT �ϐ����̕���; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; DATA SAVE.JPC; INFILE 'JPCDATA.SAS'; INPUT KC SC IC I1-I4; |
�@���̃v���O������̂悤�ɁA�f�[�^�E�t�@�C����(��ł�JPCDATA.SAS)�̎w��̍ۂɃh���C�u���A�p�X�����ȗ������ꍇ�́A�f�[�^�E�t�@�C���̓J�����g�E�f�B���N�g��(�{���ł�MYDIR)�̒��ɂȂ���Ȃ�Ȃ��B
�@CMS��SAS�ł́A�i�vSAS�f�[�^�E�Z�b�g�̎g�p�̍ۂɁAlibname�̎w�肪����Ȃ����A���̑���ACMS�t�@�C������̃f�[�^�̓ǂݍ��݂̍ۂɂ�ddname�̎w�肪�K�v�ɂȂ�(�ڂ������t�͑�2�����Q�Ƃ̂���)�BCMS�ł́A�f�[�^���͋@��̊���l�͒[���ɂȂ��Ă���̂ŁACMS�t�@�C��(fileid = fn ft [A])����f�[�^��ǂݍ��ލۂɂ́A"X CMS�R�}���h"�Ńf�[�^���͋@��̐ݒ��ύX����K�v������B
| CMS��SAS |
|---|
|
X FIledef ddname DISK fileid; DATA �i�vSAS�f�[�^�E�Z�b�g��;�@�@�@�@�@ INFILE ddname; INPUT �ϐ����̕���; |
| ��) |
|---|
|
X FI IN1 DISK JPCDATA SAS; DATA SAVE.JPC; INFILE IN1; INPUT (KC SC IC I1-I4)(2*1. 2. 4*1.); |
�@ddname�Ƃ��ĕM�҂�"18"�܂���"IN"�Ȃǂ��悭�g���B�����ł̃v���O������́APROGRAM EDITOR�E�B���h�E�ō쐬�����f�[�^�E�t�@�C���ł���CMS�t�@�C��JPCDATA SAS��ǂݍ��ނ��Ƃɂ��Ă���B
�@������ɂ���A�M�҂���ʃf�[�^�̍ۂɊ��߂�̂́A���̃t�H�[�}�b�g�`���ł���B���̌`���́A�����̕ϐ��Ƒ����̃I�u�U�[�ׁ[�V�����A�܂��ʂ̃f�[�^�������悤�ȏꍇ�A���Ƀf�[�^�E�G���g���[���O�����āA�t���b�s�B�E�f�B�X�N�⎥�C�e�[�v�Ńf�[�^���[�������悤�ȏꍇ�ɓK���Ă���BPC��SAS�ł́A�f�[�^�E�t�@�C�������������Œ�f�B�X�N�ɃR�s�[���Ă����Ȃ��Ă��AINFILE���̃f�[�^�E�t�@�C�����̎w����A�Ⴆ��
�@�@�@INFILE 'B:JPCDATA.SAS';
�ƃh���C�u�����Ŏw�肷��A���ځA�h���C�uB�̃t���b�s�B�E�f�B�X�N����f�[�^��ǂݍ��ނ��Ƃ��ł���B�Œ�f�B�X�N����ǂݍ��ނ��́A���x���Ȃ�Ƃ͂������̂́A�{���ň����悤�ȃf�[�^�ł͂��������b�P�ʂ̘b�ł���B
�@�Ƃ���ŁACMS��SAS�ł́A�����ϐ����g�p����ꍇ�ɂ́A�ӊO�ȃg���u���Ɋ������܂�邱�Ƃ�����B����́A���C���t���[���̒[����v�����^�ɂ���ẮA"$" �� "��" �ɒu��������K�v�����邽�߂ł���B���������āA�Ȃ�ׂ�"$"���g�p���Ȃ��悤��SAS�v���O�������������������ł���B�Ⴆ�A�f�[�^�͂��ׂĐ����ō쐬���A���l�ϐ��œ��͂ł���悤�ɂ�����A����ł��A�����ϐ����ǂ����Ă��g�p��������A'������'����������Ƃ�Ƃ����悤�ȍH�v�����Ă݂������悢�B
�@�ȏ�̂悤��DATA�X�e�b�v�ɑ����āAPROC�X�e�b�v�ɗl�X�ȓ��v���������s�����邽�߂�SAS�����������ƂɂȂ邪�A��ʂɂ́A����PROC�X�e�b�v��DATA�X�e�b�v�Ɣ�ׂĂ��ȒP�ŒZ���s���ōςނ��Ƃ������B�����ł́A��ԍŏ��ɂ���ׂ����v�����ł���P���W�v�݂̂��ɂ��čl���A���̗l�X�ȓ��v�����ɂ��Ă͂��ꂼ��Ή�����͂ɂ����āASAS���̎g�p�ɂ��Ď��グ�邱�Ƃɂ��悤�B
�@�P���W�v�́A���S�҂͂�������ƌy���������ł��邪�A���v�����Ƃ��Ĉ�Ԋ�{�I�ł��������Ă͂Ȃ�Ȃ��d�v�Ȃ��̂ł���B�܂��A���̒P���W�v���ʂ͕����̍쐬�̍ۂɂ́A�K���f�ڂ��Ȃ��Ă͂Ȃ�Ȃ����̈�ł���B�܂��A���ꂾ���ł͂Ȃ��A����ɂ���āA�f�[�^�E�G���g���[�̃~�X��SAS�v���O������DATA�X�e�b�v�ł̗l�X�Ȑݒ肪�������Ȃ���Ă���̂����`�F�b�N����Ƃ����Ӗ��ł��A���������Ƃ̏o���Ȃ��d�v�ȏ��������ł���B���̒i�K�ŁA���̑�R�͂ŏq�ׂ�K���̐ݒ�Ȃǂ����ۂ̓x�����z���Q�l�ɂ��Ȃ���s���Ă��܂��̂ł���B���̒P���W�v���s���Ƃ����X�e�b�v�ŔO����Ƀ`�F�b�N���s���Ă����Ȃ��ƁA��œ��v�����̂�蒼���𔗂���H�ڂɂȂ�̂ŏ\�����Ӑ[���s���Ăق����B���̒P���W�v�����Ȃ���A���ꂩ��s�����v�����ɂ��Ă̗l�X�ȃA�C�f�A�����̂ł���B
�@���v�w�̗p��ł����A�P���W�v���Ƃ�Ƃ������Ƃ́A�S�ϐ��̓x�����z�\���쐬����Ƃ������Ƃł���B����ɂ͎��̂悤�Ȃ����ȒP��SAS�������ōςށB
|
PROC FREQ; [TABLES �ϐ����̕���;]�@�@�@�@�@ [OPTIONS NOCENTER;] �@ |
| ��) |
|---|
|
PROC FREQ; �@�@�@TABLES KC SC I1--VI15; �@�@�@OPTIONS NOCENTER; |
�@�����ŁATABLES�����ȗ�����ƁA����l�ʂ�A�S�ϐ��ɂ��ēx�����z�\���쐬�����B�����S�ϐ��̓x�����z�\���K�v�Ȃ��Ƃ��ɂ́A�v���O������̂悤�ɕK�v�Ȃ��̂�����ϐ����̕��т�TABLES���̒��Ɏw�肷�邱�Ƃ��ł���B�������A�P���W�v�ł́A�v���O�����A�f�[�^�̃`�F�b�N������Ƃ����Ӗ�������A�S�ϐ��ɂ��Ă̓x�����z�\���쐬����̂������ł���B
�@�܂��AOPTIONS NOCENTER; ���w�肷��Əo�͍͂��[�Ɋčs����B���̎w����ȗ�����Əo�͉͂�ʂ̒����Ɋčs����B�o�͂�MS-DOS�t�@�C����CMS�t�@�C���ɏ����o���āA���[�v���ŕҏW����ۂɂ́AOPTIONS NOCENTER; ���w�肵�āA�o�͂����[�Ɋčs���Ă��������A�t�@�C���e�ʓI�ɂ��A��ƓI�ɂ����ʂ��Ȃ��B�����Ƃ́A���ǁA�e�s�̐擪�����ɂ�������̋�(�u�����N)��}�����邱�Ƃ�����ł���B����PROC FREQ�ɂ���č쐬�����x�����z�\�́A���̂悤�Ȍ`���ɂȂ��Ă���B
�}2.7�@PROC FREQ�ɂ���č쐬�����x�����z�\�̈�ʌ`��
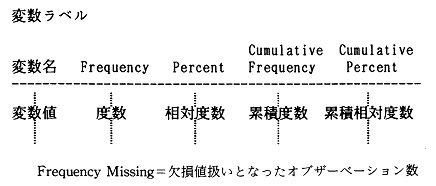
�@�x�����z�\�̌`����ǂݕ��ɂ��ẮA������3���Ő�������̂ŁA�����ł͂Ƃ肠�����A�P���W�v�Ƃ́A���̓x�����z�\�A���̒��ł����ɁA�x���Ƒ��Γx�������߂邱�Ƃ��Ƃ������Ƃ����������Ă������B���̂悤�ȓx�����z�\�̌`�œ���ꂽ�P���W�v���ʂŊm�F���ׂ����Ƃ��A������x�܂Ƃ߂Ă������B
�@�����ł́A���⒲���[�̉̃f�[�^�E�G���g���[�ƒP���W�v�̍쐬�A�����č���̓��v�����ɍė��p����i�vSAS�f�[�^�E�Z�b�g�̐�������Ƃ̏��Ɏ��グ��B�܂��A�f�[�^�E�G���g���[����n�߂悤�B
�@��{�^SAS�v���O�����̒��Ńf�[�^�E�t�@�C���Ƃ��Ďw�肷�邱�ƂɂȂ�MS-DOS�t�@�C��JPCDATA.SAS�A���邢��CMS�t�@�C��JPCDATA SAS�������ō쐬����ꍇ���l���Ă݂悤�B�f�[�^�E�t�@�C���͎����̎g���₷�����[�v���E�\�t�g�ō���Ă��悢���A�����ł́A��������PROGRAM EDITOR�E�B���h�E�̎g��������������̂ŁA����PROGRAM EDITOR�E�B���h�E�ō쐬���Ă݂悤�B�f�[�^�E�t�@�C���쐬�͂������ĊȒP�ł���B�}2.7�ł́A�f�[�^��Ƃ��āA��6���Ŏ���Ƃ��Ď��グ��u�g�D�������̂��߂̏]�ƈ��ӎ������v�̎��ۂ̉̂����A20�l���̃f�[�^��PROGRAM EDITOR�E�B���h�E�œ��́A�쐬���Ă���Ƃ����2��ʂŗᎦ���Ă���B
�}2.8�@PROGRAM EDITOR�E�B���h�E�ō쐬����f�[�^�E�t�@�C���̈ꕔ(20�l��)
�@�@�@(MS-DOS�t�@�C��JPCDATA.SAS�A���邢��CMS�t�@�C��JPCDATA SAS)

�@����PROGRAM EDITOR�E�B���h�E�ł̓��͍�Ƃ��I������A�R�}���h�s�ɁAPC��SAS�̂Ƃ���
�@�@�@Command ===> FILE 'JPCDATA.SAS'
CMS��SAS�̂Ƃ���
�@�@�@Command ===> FILE 'JPCDATA SAS'
�Ɠ��͂��āAMS-DOS�t�@�C��JPCDATA.SAS (�f�B���N�g���͎����I�ɃJ�����g�E�f�B���N�g��MYDIR�ɂȂ�)�܂���CMS�t�@�C��JPCDATA SAS�̒��ɕۑ����Ă������B�����Ƃ��A���͂��I��܂ŕۑ����Ȃ��Ƃ����̂́A���������g���u�����������Ƃ��ɁA����܂ł̃f�[�^�E�G���g���[�̋�J�����̖A�ƂȂ��Ă��܂��A�댯�Ȃ̂ŁA��Ɠr���ɉ��x���A����file�R�}���h���g���āA���܂߂Ƀt�@�C���ւ̕ۑ���Ƃ��s���Ă�������������ł���B
�@���ۂɂ́A�f�[�^�E�t�@�C��JPCDATA.SAS���邢��JPCDATA SAS�̒��ɂ́A907�l��1814�s�̃f�[�^�����邱�ƂɂȂ�킯����(�t�@�C���e�ʂƂ��Ă�82,538�o�C�g)�A���ꂾ���̗ʂɂȂ�ƁA�M���ł���f�[�^�E�G���g���[�Ǝ�(�̂̓J�[�h�E�p���`���O������Ƃ������Ƃ���u�p���`�Ǝҁv�Ƃ����Ă���)�ɊO�����������A�^�C�v�E�~�X���Ȃ����S�ł���B�������A���̂킸��20�l���ł����ۂɎ����̎�œ��͂��Ă݂�ƁA
�@�ł��V���v���ŊȒP�Ȋ�{�^SAS�v���O�����̗�͐}2.9�̂悤�Ȃ��̂ɂȂ�B�}2.9�͂��̊�{�^�v���O������PROGRAM EDITOR�E�B���h�E�ō쐬������Ԃ������Ă���B����͊�{�^�Ƃ͂������̂́A��6���Œ����̎���Ƃ��ċ�����u�g�D�������̂��߂̏]�ƈ��ӎ������v�ɂ���ē���ꂽ�f�[�^�����ۂɒP���W�v���A�i�vSAS�f�[�^�E�Z�b�g�����邱�Ƃ��ł���SAS�v���O�����ł���B�V���v���ł͂��邪�A����ł��̖�ڂ��\���ɉʂ������ƂɂȂ�B
�}2.9�@PROGRAM EDITOR�E�B���h�E�ō쐬������{�^SAS�v���O����(PC��SAS)
�@�@�@(MS-DOS�t�@�C��JPCP0.SAS�A���邢��CMS�t�@�C��JPCP0 SAS�ɕۑ�)

�@�}2.9��PC��SAS�p�̃v���O�����ł��邪�ACMS��SAS�p��1�s�ځA3�s�ڂ����ꂼ�ꎟ�̂悤�ɒu��������悢�B
�@�@�@00001 X FI IN1 DISK JPCDATA SAS;
�@�@�@00003 INFILE IN1;
�@���̊�{�^SAS�v���O�����́APROGRAM EDITOR�E�B���h�E�ō쐬������A��͂�file�R�}���h�ŁAMS-DOS�t�@�C��JPCP0.SAS�A���邢��CMS�t�@�C��JPCP0 SAS�ɕۑ����Ă����B
�@���Ĉȏ�̏�������������A��������SAS�v���O���������s���Ă݂悤�B���܂������A����SAS�v���O�����̎��s�ɔ����āA���X��LOG�E�B���h�E�ɕ\��������āA���s�I�����ɂ́A�}2.10�̂悤�ȕ\�����o����Ă���͂��ł���B
�}2.10�@��{�^SAS�v���O���������s�����Ƃ���LOG�E�B���h�E�̕\��(PC��SAS)
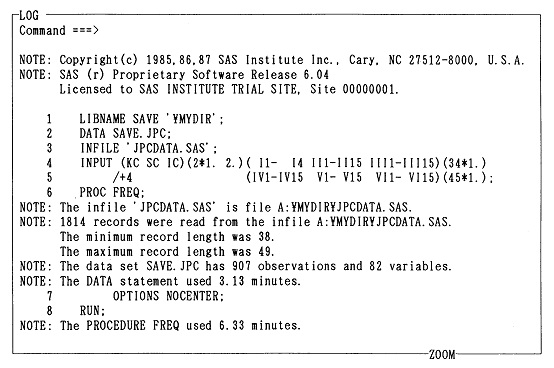
�@���̃��O�̓��e������킩��悤�ɁAPC��SAS�ł́A����SAS�v���O�����̎��s���Ԃ��\�������B���̗�ł́A���s�ɂ͌v10�����v�������Ƃ��킩��(�����Ƃ��A�܂���������SAS�v���O�����ł��A���̎��s���Ԃ͎��s�̓x�ɐ��b���x�̂�����o��)�B���̌��ʁA���������i�vSAS�f�[�^�E�Z�b�gJPC.SSD��607,528�o�C�g�܂��600KB�̑傫����MS-DOS�t�@�C���ƂȂ�BCMS��SAS�ł́A���s���Ԃ͕\������Ȃ����A�͂邩�ɒZ���ԂŎ��s���I��A�i�vSAS�f�[�^�E�Z�b�gJPC SAVE�����������B
�@�P���W�v�̌��ʂ́AOUTPUT�E�B���h�E�Ɏ��X�ƕ\������邪�A���̂����̈��ʕ����o���ƁA�}2.11�̂悤�ɂȂ�B
�}2.11�@��{�^SAS�v���O���������s���ē���ꂽ�o�͂̈ꕔ��\������OUTPUT�E�B���h�E

�@����I 1�͐��ʂɊւ�����̂ŁA���̏ꍇ�A1�͒j�ŁA2�͏���\���Ă���B����ȊȒP�ȒP���W�v�ł����Ă��A�]�ƈ��i���Ј��j�̑������j���ł���Ƃ������{�̑��Ƃɂ�����z���C�g�J���[�̐E��̎��Ԃ��_�Ԍ�����B
�@�ȏ�̊�{�^SAS�v���O�����́A�P���W�v�p�v���O�����̒��ł��ł��ȒP�Ȃ��̂ł���B����ł��\���Ɏ��p�ɂȂ邪�A�M�҂����ۂɒ����̍ۂɗp����ʏ�^SAS�v���O�����ł́A�o�͌��ʂ��킩��₷�����邽�߂ɕϐ��Ƀ��x����������A��X�s�����v�����̂��ƂȂǂ��l���āA�����̕ϐ������Ƃɂ��ėl�X�ȃf�[�^�̉��H�A�������s�����肵�Ă����ƂƂ��ɁA�o�͌��ʂ����[�h�E�v���Z�b�T�[�ŕҏW����ۂ̍�Ƃ����₷������悤�ȗl�X�ȍH�v���{���Ă���B�����ŁA���̐߂ł́A���̍ł��V���v���Ȋ�{�^SAS�v���O�������x�[�X�ɂ��āA���ۂ̒����ɗp������P���W�v�p�̒ʏ�^SAS�v���O�����ւƐi�������Ă݂悤�B
�@�ϐ��ɂ͕ϐ��������ł͂Ȃ��A�ϐ��̐����̂��߂Ƀ��x�������邱�Ƃ��ł���B�ϐ��̃��x����40����(�o�C�g)�ȓ��ŁA���̂悤�Ȍ`���Ŏw�肷�邱�Ƃ��o����B
|
LABEL �ϐ���1='���x��1' �ϐ���2='���x��2' �c�c;�@ �@ |
| ��) |
|---|
|
LABEL KCODE='COMPANY' SCODE='UNIT' �@�@�@ I1='SEX'�@I2='AGE'�@I3='OCCUPATION'�@I4='RANK'; |
�@���x�����ꎩ�̂̒��Ɂu'�v���܂߂����Ƃ��́u''�v��2�����ď����ƁASAS�ł�1�ƔF������A�\������邱�ƂɂȂ�B
�@�ϐ��̃��x���ɓ��{��f�[�^(�S�p����)���g�����Ƃ��o����B�������A�M�҂Ƃ��ẮA���ɁACMS��SAS�ł́ASAS�v���O�����̒i�K�őS�p�������g�p���邱�Ƃ͊��߂��Ȃ��B���ۂ̌o�����炷��ƁA�v���O�����i�K�œ��{��f�[�^���܂߂Ă����ƁAOS��C���t���[���̒[���̎�ށA���{��ϊ��v���Z�b�T�[�̂�����\�ɂ���āA�������e���e�����A�v�������Ȃ��g���u���̌����ɂȂ邩��ł���B�������AIBM�̃��C���t���[���ł́A�V�t�g�E�R�[�h�őS�p�������͂��ޕK�v������̂ŁA���̂Ƃ��ɂ̓��x����19�����ȓ��Ƃ������ƂɂȂ邾���ł͂Ȃ��A���̃V�t�g�E�R�[�h���f�[�^�̓]����[�h�E�v���Z�b�T�[�ɂ��ҏW�̍ۂɃg���u���̌����ɂȂ�̂ł���B�o�͌��ʂ̐}�\�Ń��x���Ƃ��ē��{���p�������̂ł���A�o�͂������o����MS-DOS�t�@�C����ҏW����ۂɁA���{�ꃏ�[�h�E�v���Z�b�T�[�̕ҏW�@�\���g���āA���{�ꃉ�x���ɒu�����Ă����������͂邩�Ɋm���A���p�I�ł������B
�@�ϐ��ɕϐ��l�������邱�Ƃ́A���蓖�ĕ�(assignment statement)�ɂ���čs����B���蓖�ĕ��Ƃ����Ă��A�`���͂������ĊȒP�ŁA
| �ϐ���=��;�@ |
�@�萔�͐��l�f�[�^�ł������f�[�^�ł��悢�B���l�f�[�^�̏ꍇ�ɂ́A���ڐ��l��������悢���A�����f�[�^�̏ꍇ�ɂ́A���̕����f�[�^��'�@'�ň͂�ŁA���ꂪ�����f�[�^�ł��邱�Ƃ�����K�v������B��̓I�ɂ͎��̂悤�Ȍ`���ɂȂ�B
|
�ϐ���=���l;�@ |
| ��) |
|---|
| TI1=1; |
|
�ϐ���='������';�@ |
| ��) |
|---|
| I1='1.MALE '; |
�@����I�u�U�[�x�[�V�������ł̕ϐ��l�̉��Z�l��^����ꍇ�ɂ́A��̓I�ɂ͕ϐ������g���������̌`�Ŏ����悢�B
|
�ϐ���=����;�@ |
| ��) |
|---|
| SCODE=KC*10+SC; |
�Ƃ����`���ɂȂ�B��������Ɗe�I�u�U�[�ׁ[�V�����̕ϐ��l���g���ĉ��Z���s���A���̉��Z���ʂ̒l���ϐ��ɑ�������B��ł́A�e�I�u�U�[�ׁ[�V�����ŁA�ϐ�KC, SC�̒l���g���ĉ��Z���s���A���̉��Z���ʂ̒l���ϐ�SCODE�ɑ������邱�ƂɂȂ�B�܂�A��ЃR�[�h���\�̈ʂɁA��Ђ��Ƃɕt����ꂽ�g�D�P�ʃR�[�h����̈ʂɂ��A�S��Ђ�ʂ��Ďg����2���́u�g�D�P�ʃR�[�h�v��^���Ă���̂ł���B
�@�Z�p���Z�q�̗D�揇�ʂ�
�@�����P���ɓ����������J��Ԃ��̂ł͂Ȃ��A�ϐ��l�ɂ���ď����ʂɏ�����I�����邱�Ƃ��ł���B����ɂ�SELECT/WHEN�����p������BSELECT/WHEN���ł́AWHEN�ŏ����������A���̏������^�̂Ƃ����������s�����B����3�͎��ۂɂ͂Ȃ��Ă��AOTHERWISE�͕K������Ă������Ƃɒ��ӂ��Ăق����B
|
SELECT; WHEN(������1)����1;�@�@�@�@�@ WHEN(������2)����2; �c�c�@�@�@ OTHERWISE[����3]; END; |
| ��) |
|---|
|
SELECT; �@WHEN(TI1=1) I1='1.MALE '; �@WHEN(TI1=2) I1='2.FEMALE'; �@OTHERWISE I1=' '; �@END; |
�@���̃v���O������͕ϐ��l���x���̒�`�����Ă�����̂ł���B�v���O������̒��ŁATI1=1�Ƃ�TI1=2�Ƃ�����̂́A�l�̑�����̈Ӗ��ł͂Ȃ��āA�����������_�����ł���B���̗�̂悤�ɁA�������͎��̂悤�ȉ��Z�q���g���ď����ꂽ�^�U�̔���ł���_�����ł���B
| ��r���Z�q�@ | �@EQ�@ | �@NE�@ | �@GT�@ | �@GE�@ | �@LT�@ | �@LE�@ |
| �܂��� | = | �@ | > | >= | < | <= |
| �_�����Z�q�@ | �@AND�@ | �@OR�@ | �@NOT�@ | ||||||||||
| �܂��� | & | | | |||||||||||
|
SELECT(�ϐ���); WHEN(�ϐ��l1)����1;�@�@�@�@�@ WHEN(�ϐ��l2)����2; �c�c�@�@�@ OTHERWISE[����3]; END; |
| ��) |
|---|
|
SELECT(TI1); �@WHEN( 1 ) I1='1.MALE '; �@WHEN( 2 ) I1='2.FEMALE'; �@OTHERWISE I1=' '; �@END; |
�@����SELECT/WHEN���̏����͂��̂悤�ȕϐ��l�̑�������ł͂Ȃ��A�l�X�ȏ������\�ł���B��̓I�ɑ����p�����鏈���̃P�[�X�Ƃ��Ă͎��̂悤�Ȃ��̂�����B
�@�����Ƃ���ʓI�ł悭�g����B���Ɍ��Ă����ϐ��l���x���̒�`������ɂ�����B�������A���ӂ��Ȃ���Ȃ�Ȃ��̂́A�����ϐ��̒l�́A�o�͂̕\���ɕ\�������Ƃ��ɂ͏����ɕ��ׂ���Ƃ������Ƃł���B���ꂽ�߂ɁA�p������n�܂�ϐ��l���f�[�^�Ƃ��ė^���A���x������Ɏg�p����ۂɂ͎��������ƂȂ��Ă��܂��B�����������邽�߂ɂ́A��قǂ̃v���O������ɂ����� '1.MALE', '2.FEMALE' �̂悤�ɁA�ŏ��ɐ���������Ɨǂ��B
�@�܂���3���ł��q�ׂ�K���̒�`���ϐ��l���x���̒�`�Ɠ��l�Ɏ��̗�̂悤�ɍs���B
| ��) |
|---|
|
SELECT; �@WHEN (20<=I2<25) LI2='20-24'; �@WHEN (25<=I2<30) LI2='25-29'; �@WHEN (30<=I2<35) LI2='30-34'; �@WHEN (35<=I2<40) LI2='35-39'; �@WHEN (40<=I2<45) LI2='40-44'; �@WHEN (45<=I2<50) LI2='45-49'; �@WHEN (50<=I2<55) LI2='50-54'; �@WHEN (55<=I2<60) LI2='55-59'; �@OTHERWISE LI2=' '; �@END; |
�@�܂��ϐ��l���x����10����(�o�C�g)�ȉ��ɗ}���������APROC�Ńg���u�����N���Ȃ��B10�������z�������́A�N���X�\�Ȃǂł͖��������B
| DELETE;�@ |
�@SELECT/WHEN���̏����Ƃ��āA�I�u�U�[�ׁ[�V�����̍폜��p����ƁA�����ɂ������I�u�U�[�ׁ[�V�����������c���ē��v���������邱�Ƃ��\�ɂȂ�B�Ⴆ�A�����ΏۑS�̂��������̃T�u�O���[�v�ɕ����Ă��ꂼ��̓����l�����߂�悤�ȍۂɂ͕K�v�ƂȂ�B�������A����DELETE�����i�vSAS�f�[�^�E�Z�b�g�ɗp����ƁA�I�u�U�[�ׁ[�V�����͉i�v�ɏ����Ă��܂��̂ŁA�T�u�O���[�v���Ƃ̓��v���Ƃ邽�߂ɂ͈ꎞSAS�f�[�^�E�Z�b�g�ɂ���DELETE�����g���Ă��邱�Ƃ��m�F���Ȃ���g�p���������悢((6)��(b)���Q�Ƃ̂���)�B
�@DO�O���[�v�́ADO;��END;�ł͂��܂ꂽSAS���Q�ŁASAS�ł�DO-END����DO�O���[�v�����SAS���̂悤�Ɉ����B����SELECT/WHEN����WHEN���ɑ����ď�����鏈���́A�`���I�ɂ͈�̏������������Ȃ��悤�ɂȂ��Ă���B�����ŁA������SAS�������s���������Ƃ��ɁADO�O���[�v�̌`���Ƃ��āA�`���I�Ɉ�̏����Ƃ��Ď��߂Ă��܂����Ƃ����킯�ł���B���̗�ł́A��������DO�O���[�v�ɂȂ��Ă���B
|
DO; SAS���Q END; |
| ��) |
|---|
|
SELECT; �@WHEN(KC=1) KCODE='1.A '; �@WHEN(KC=2) KCODE='2.B '; �@OTHERWISE DO; KCODE=' ';SC=.; KC=.; IC=.; END; �@END; |
�@�����SELECT/WHEN�������q�̌`�Ŏg�p���邱�Ƃ��\���Ƃ������Ƃł���B
�@�قȂ�ϐ��ɁA���x�������������J��Ԃ��ꍇ�́A������������������Ă��ẮA�v���O��������������ɒ����Ȃ��Ă��܂����A������ɂ����Ȃ��Ă��܂��B���������ꍇ�ɂ́A���̂悤��ARRAY����p����ƕ֗��ł���B
|
ARRAY �ϐ���{n} �ϐ����̕���; DO I=1 TO n; �@�@�@�ϐ���{I}���܂����@�@�@ END; |
| ��) |
|---|
|
ARRAY TYN{15} TII1-TII15; ARRAY YN{15} $ II1- II15; DO I=1 TO 15; �@SELECT; WHEN(TYN{I}=1) YN{I}='1.YES'; �@�@�@�@�@WHEN(TYN{I}=2) YN{I}='2.NO '; �@�@�@�@�@OTHERWISE YN{I}=' ';END; END; |
������n�ɂ́A�ϐ����̕��тɂ���ϐ��̌��𐔒l�Ƃ��ē����B�v���O�������ARRAY����2�s�ڂɂ�����悤�ɁA�ϐ��ɕ����萔��������ہAARRAY���̒��ŁA���̕ϐ��̑O�ɕ����ϐ��ł��邱�Ƃ�����"$"�����邱�Ƃ�Y��Ȃ��悤�ɂ���B
�@����ł́A�ȏ�ɏq�ׂĂ����悤�ȗl�X��SAS������g���āA�f�[�^�̓��͂�ϐ����A�ϐ����x���̐ݒ���s���A�i�vSAS�f�[�^�E�Z�b�g���쐬����ƂƂ��ɁA�P���W�v���s���ʏ�^SAS�v���O�����̗���A�܂�PC��SAS�p�Ɏ������Ƃɂ��悤�B
*-----------------------------------------------------;
*-----------------------------------------------------;
*JPCP1.SAS ;
* Permanent SAS data set JPC.SSD will be made. ;
*-----------------------------------------------------;
*-----------------------------------------------------;
LIBNAME SAVE '��MYDIR';�@�@�@�@�@�@�@�@�@�@�@�@�@(i)
DATA SAVE.JPC;
*-----------------------------------------------------;
* Raw data will be read from MS-DOS file JPCDATA.SAS. ;
*-----------------------------------------------------;
INFILE 'JPCDATA.SAS';�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(ii)
INPUT (KC SC IC)(2*1. 2.)
(TI1-TI4 TII1-TII15 TIII1-TIII15)(34*1.)
/+4 (TIV1-TIV15 TV1-TV15 TVI1-TVI15)(45*1.);
*-----------------------------------------------------;
* KCODE SCODE will be made. ;
*-----------------------------------------------------;
SELECT;
WHEN(KC=1) KCODE='1.A ER ';
WHEN(KC=2) KCODE='2.B STORE ';
WHEN(KC=3) KCODE='3.C RAIL ';
WHEN(KC=4) KCODE='4.D EP ';
WHEN(KC=5) KCODE='5.E SER ';
WHEN(KC=6) KCODE='6.F BANK ';
WHEN(KC=7) KCODE='7.G HI ';
WHEN(KC=8) KCODE='8.H OIL ';
OTHERWISE DO; KCODE=' '; SC=.; IC=.; END;
END;
SCODE=KC*10+SC;
*-----------------------------------------------------;
* Classification data will be labeled. ;
*-----------------------------------------------------;
SELECT;
WHEN(TI1=1) I1='1.MALE ';
WHEN(TI1=2) I1='2.FEMALE';
OTHERWISE I1=' ';
END;
SELECT;
WHEN(TI2=1) I2='1.20-24';
WHEN(TI2=2) I2='2.25-29';
WHEN(TI2=3) I2='3.30-34';
WHEN(TI2=4) I2='4.35-39';
WHEN(TI2=5) I2='5.40-44';
WHEN(TI2=6) I2='6.45-49';
WHEN(TI2=7) I2='7.50-54';
WHEN(TI2=8) I2='8.55-60';
OTHERWISE I2=' ';
END;
SELECT;
WHEN(TI3=1) I3='1.STAFF';
WHEN(TI3=2) I3='2.E & P';
WHEN(TI3=3) I3='3.R & D';
WHEN(TI3=4) I3='4.SALES';
OTHERWISE I3=' ';
END;
SELECT;
WHEN(TI4=1) I4='1.GEN ';
WHEN(TI4=2) I4='2.MGR ';
WHEN(TI4=3) I4='3.HEAD ';
WHEN(TI4=4) I4='4.OTHERS';
OTHERWISE I4=' ';
END;
ARRAY TYN{75} TII1--TVI15;
ARRAY YN{75} $ II1-II15 III1-III15 IV1-IV15 V1-V15 VI1-VI15;
DO I=1 TO 75;
SELECT; WHEN(TYN{I}=1) DO; TYN{I}=1; YN{I}='1.YES'; END;
WHEN(TYN{I}=2) DO; TYN{I}=0; YN{I}='2.NO '; END;
OTHERWISE DO; TYN{I}=.; YN{I}=' '; END; END;
END;
LABEL
KCODE='COMPANY'
SCODE='UNIT'
I1='SEX'
I2='AGE'
I3='OCCUPATION'
I4='RANK';
*-----------------------------------------------------;
* Check the labels and the frequencies. ;
*-----------------------------------------------------;
PROC FREQ;
OPTIONS NOCENTER;
RUN;
�@���̃v���O������MS-DOS�t�@�C��JPCP1.SAS�ɕۑ����Ă������B���ꂪ�A��6���Œ����̎���Ƃ��Ă�����u�g�D�������̂��߂̏]�ƈ��ӎ������v�̍ۂɒP���W�v�Ɖi�vSAS�f�[�^�E�Z�b�g�����Ɏ��ۂɗp����ꂽSAS�v���O�����ł���B
�@��قǂ̊�{�^SAS�v���O�����Ɠ����A�f�[�^�̓�����MS-DOS�t�@�C��JPCDATA.SAS����A�i�vSAS�f�[�^�E�Z�b�g�����������B�i�vSAS�f�[�^�E�Z�b�g���ɓ���JPC���g���Ă���̂ŁAMS-DOS�t�@�C��JPC.SSD�͏d�ˏ�������A���e�͍X�V����邱�ƂɂȂ�B�������ԂƂ��ẮADATA�X�e�b�v��6�����APROC�X�e�b�v�ł͖�9���������ɗv����B���������āA�S�̂ł�15�����Ƃ������ƂɂȂ�B���̌��ʁA���������i�vSAS�f�[�^�E�Z�b�gJPC.SSD��1,211,212�o�C�g�܂��1.2MB�̑傫����MS-DOS�t�@�C���ƂȂ�B��{�^SAS�v���O������82�ϐ��ɑ��āA���̒ʏ�^SAS�v���O�����ł�164�ϐ�����`����邱�ƂɂȂ�̂ŁA��{�^SAS�v���O�����̖�2�{�̃t�@�C���e�ʂ�K�v�Ƃ��邱�ƂɂȂ�B
�@CMS��SAS�p�̃v���O�����́A����PC��SAS�p�̃v���O�����̂����̂킸��2�s�A(i)��(ii)�����̂悤�ɒu��������悢�B
�@�i�vSAS�f�[�^�E�Z�b�g�͈�x�쐬���Ă��܂��A�����f�[�^�̓ǂݍ��݂�ϐ��̒�`�A�f�[�^�̉��H���J��Ԃ��K�v�͂Ȃ��A���Ƃ͂����ʂ̃v���O�����̒��ŌĂяo���Ă�邾���ŁASAS�͂���SAS�f�[�^�E�Z�b�g���Q�Ƃ��āAPROC�X�e�b�v���s�����Ƃ��ł���B���������āA�����̉i�vSAS�f�[�^�E�Z�b�g���g��SAS�v���O�����́A�Ȍ����ȒP�Ȃ��̂ōς܂��邱�Ƃ��ł���B������3���ȍ~�Ŏ��グ��SAS�v���O�����́A���̂��߂ɁA�����ȒP�Ȃ��̂ɂȂ�B�����ł͉i�vSAS�f�[�^�E�Z�b�g���J��Ԃ��čė��p����ۂ̈�ʓI�ȕ��@�ɂ��Ă܂Ƃ߂Ă������B�i�vSAS�f�[�^�E�Z�b�g�̌Ăяo���͎��̂悤�ɍs���B
�@PC��SAS�ŁA�i�vSAS�f�[�^�E�Z�b�g��1�̉i�vSAS�f�[�^�E�Z�b�g�̓ǂݍ��݂��s���A�܂��V���ɒ�`�����ϐ���A�V���ɉ��H���ꂽ�f�[�^���܂߂āA�i�vSAS�f�[�^�E�Z�b�g��2�̉i�vSAS�f�[�^�E�Z�b�g�ɏ����o���ɂ͎��̂悤�ɂ���悢�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; DATA libname.�i�vSAS�f�[�^�E�Z�b�g��2�{��;�@ SET libname.�i�vSAS�f�[�^�E�Z�b�g��1�{��; �@�@�@�f�[�^�̉��H�E���� �@�@�@ |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; DATA SAVE.JPC; �@�@SET SAVE.JPC; SELECT; WHEN(TI1=1) I1=1; �@�@�@�@WHEN(TI1=2) I1=0; �@�@�@�@OTHERWISE I1=.; END; END; |
�������邱�ƂŁASAS�f�[�^�E�Z�b�g�͉i�vSAS�f�[�^�E�Z�b�g�ƂȂ�ADATA�X�e�b�v�ōs�������H�����́A���̂܂�MS-DOS�t�@�C���Ƃ��ĕۊǂ���邱�ƂɂȂ�B���̃v���O������̂悤�ɓ�̉i�vSAS�f�[�^�E�Z�b�g�����ɂ���ƁA�v���O�������s�̓s�x�A�i�vSAS�f�[�^�E�Z�b�g�͏����������A�X�V����邱�ƂɂȂ�BDATA����SAS�f�[�^�E�Z�b�g��2���i�vSAS�f�[�^�E�Z�b�g��1�ƕʂ̂��̂ɂ���A�V���ɂ�����ʂ̉i�vSAS�f�[�^�E�Z�b�g�������I�ɐ��������B
�@CMS��SAS�ł́APC��SAS�̂悤��libname�̎w�肪����Ȃ��B�܂�CMS��SAS�ł�1�s�ڂ�LIBNAME���͂����ɁA2�s�ڂ�DATA������n�߂�킯�����A���̍ہAPC��SAS��DATA������libname�ɑ���������̂Ƃ��āACMS��SAS�ł͉i�vSAS�f�[�^�E�Z�b�g����ft���w�肷�邱�ƂɂȂ�B���̂��߁A�i�vSAS�f�[�^�E�Z�b�g����ft.fn ��ft����ɂ��邱�Ƃɒ��ӂ���BCMS��SAS�ł́A���̂悤�Ɏw�肷�邾���ŁCSAS�f�[�^�E�Z�b�g�͉i�vSAS�f�[�^�E�Z�b�g�ƂȂ�ADATA�X�e�b�v�ōs�������H�����́A���̂܂�CMS�t�@�C���Ƃ��ĕۊǂ���邱�ƂɂȂ�B���������āA�`���I�ɂ́A�v���O������ŁA1�s�ڂ��폜�������̂��A���̂܂�CMS��SAS�̃v���O������ƂȂ�B���Ȃ킿�A�i�vSAS�f�[�^�E�Z�b�g��1�̉i�vSAS�f�[�^�E�Z�b�g�̓ǂݍ��݂��s���A�܂��i�vSAS�f�[�^�E�Z�b�g��2�̉i�vSAS�f�[�^�E�Z�b�g�ɏ����o���ɂ͎��̂悤�ɂ���悢�B
| CMS��SAS |
|---|
|
DATA �i�vSAS�f�[�^�E�Z�b�g��2;�@ SET �i�vSAS�f�[�^�E�Z�b�g��1; �@�@�@�f�[�^�̉��H�E���� �@�@�@ |
| ��) |
|---|
|
DATA SAVE.JPC; �@SET SAVE.JPC; SELECT; WHEN(TI1=1) I1=1; �@�@�@�@WHEN(TI1=2) I1=0; �@�@�@�@OTHERWISE I1=.; END; END; |
�����ŁA�v���O������ł�ft��SAVE�ɂ��Ă��邪�A����͑��̂��̂ɂ��Ă������B�������A����ft��WORK�ɂ���ƁA�ꎞSAS�f�[�^�E�Z�b�g�Ƃ��ĔF������Ă��܂��̂ŁA����ȊO�̂��̂ɂ��邱�ƁB
�@�i�vSAS�f�[�^�E�Z�b�g�̓ǂݍ��݂������s���A�i�vSAS�f�[�^�E�Z�b�g��������������A�����o�����肷��悤�Ȃ��Ƃ͂������Ȃ��Ƃ��ɂ́A���̂悤��DATA���ňꎞSAS�f�[�^�E�Z�b�g���w�肵�āA���̒��ɁA��]����i�vSAS�f�[�^�E�Z�b�g��ǂݍ���ł���`���Ƃ�悢�B(a)�Ƃ̈Ⴂ�́APC��SAS�ł�DATA���̒���libname�̗L�������ACMS��SAS�ł͓�����DATA����SAS�f�[�^�E�Z�b�g����ft�̗L�������ł���B
| PC��SAS |
|---|
|
LIBNAME libname '�f�B���N�g����'; DATA �ꎞSAS�f�[�^�E�Z�b�g��;�@�@�@�@�@�@ SET libname.�i�vSAS�f�[�^�E�Z�b�g���{��; �@�@�@�f�[�^�̉��H�E���� �@�@�@ |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; DATA�@�@�@�@JPC; �@�@SET SAVE.JPC; SELECT; WHEN(TI1=1) I1=1; �@�@�@�@OTHERWISE�@DELETE; �@�@�@�@END; |
| CMS��SAS |
|---|
|
DATA �ꎞSAS�f�[�^�E�Z�b�g��;�@�@�@�@�@�@ SET �i�vSAS�f�[�^�E�Z�b�g��; �@�@�@�f�[�^�̉��H�E���� �@�@�@ |
| ��) |
|---|
|
DATA�@�@�@�@JPC; �@�@SET SAVE.JPC; SELECT; WHEN(TI1=1) I1=1; �@�@�@�@OTHERWISE�@DELETE; END; |
�@���̏͂ł�SAS��6�ł̎g�p���@��������Ă������A�ŐV�ł̑�6�ł������[�X����Ă܂��Ԃ��Ȃ����A���݂ł�IBM�̃��C���t���[����IBM�݊����Y���C���t���[���̈ꕔ�ł́ASAS��5�ł̍ŐV�łł����������[�X5.18�����̂܂g�p����Ă���Ƃ��������悤�Ȃ̂ŁA���̐߂ł́ACMS��SAS�����[�X5.18�̊�{�I�Ȏg�p���@�ɂ��ĊT�����Ă������B�����Ƃ��ACMS��SAS�̑�6�łƂ̑���_�́A�f�B�X�v���C�E�}�l�[�W���E�V�X�e���̎g�p���@�Ɋւ�����̂����S�ł���B
�@SAS���N������ƁA�v���O�����쐬�A���s�̂��߂̃V�X�e�����N������āACMS��SAS�̑�5�łł́A�[���̃f�B�X�v���C��ʂɐ}2.12�̂悤�ȕҏW�^���O��ʂ��\�������B����͍\���I�ɂ�CMS��SAS�̑�6�ł̃E�B���h�E�Ɗ�{�I�ɂ͓����ł���B
�}2.12�@CMS��SAS�����[�X5.18�̃f�B�X�v���C�E�}�l�[�W���E�V�X�e���̉��

�@CMS��SAS��6�łƓ��l�ɁAkeys�R�}���h���g����̂ŁA���̕ҏW�^���O��ʂ�PF�L�[(�t�@���N�V�����E�L�[)�̐ݒ�́A�����Ŋm�F���邱�ƁBCMS��SAS�̑�6�łƂ̈Ⴂ�����ɋ����Ă����B���̑��ɂ��Ă͂��܂�Ⴂ�͂Ȃ��B
�@�o�͉�ʂ�file�R�}���h���g���Ȃ����Ƃ���A�o�͂�CMS�t�@�C���ɕۑ��������ꍇ�ɂ́A���ځA�o�͂�CMS�t�@�C���ɑ��čs�������Ȃ��B�����ɏq�ׂ���@�́ACMS��SAS��6�łł����̂܂g����(�����Ƃ����̕K�v�͂Ȃ����낤���c�c)�B
�@CMS�ł́A�f�[�^���o�͋@��̊���l�͒[���ɂȂ��Ă���̂ŁACMS�t�@�C���ɏo�͂���ꍇ�ɂ��ACMS�t�@�C������f�[�^��ǂݍ��ލۂƓ��l�ɁA"X CMS�R�}���h" �Őݒ��ύX���Addname���w�肷�邱�Ƃ��K�v�ɂȂ�B��̓I�ɂ́ACMS�t�@�C��(�v���O������ł́Afileid=JPC LST [A])���ʂ��o�͂������Ǝv���Ă���PROC���̑O�ցA����2�s��}������Ƃ悢�B
|
X FIledef ddname DISK fileid;�@ PROC PRINTTO UNIT=ddname; |
| ��) |
|---|
|
X FI 18 DISK JPC LST; PROC PRINTTO UNIT=18; |
"UNIT=" �ɂ͑��u�ԍ������g���Ȃ��̂ŁA�M�҂�ddname�Ƃ���18���悭�g��(11�`15�͎g���Ȃ�)�B����fileid��CMS�t�@�C�������ɑ��݂��Ă���ꍇ�ɂ́A�d�ˏ�������Ă����̂Œ��ӂ�����B�܂��A����PROC���̌�ŏo�͋@��̐ݒ��[���ɖ߂��ɂ͎��̈ꕶ������B
| PROC PRINTTO;�@ |
���̕����Ȃ���Γ�SAS�Z�b�V�������͐ݒ�ύX�����������邱�ƂɂȂ�B
�@������SAS������5��(5)�̊�{�^SAS�v���O�����ɂ́A���̉������̂悤�ɑ}�������B
X FI IN1 DISK JPCDATA SAS;
DATA SAVE.JPC;
INFILE IN1;
INPUT (KC SC IC)(2*1. 2.)(TI1 -TI4 TII1-TII15 TIII1-TIII15)(34*1.)
�@�@�@/+4�@�@�@�@�@�@�@(TIV1-TIV15 TV1 -TV15 TVI1 -TVI15 )(45*1.);
X FI 18 DISK JPC LST;
PROC PRINTTO UNIT=18;
PROC FREQ;
�@�@�@OPTIONS NOCENTER;
PROC PRINTTO;
RUN;
2.1 ��{�^SAS�v���O�����̎��s �@��5��(5)�Ɏ������ʂ��SAS�v���O�������쐬�A���s���āA�P���W�v���s���Ă݂�B���̍ۂ̃f�[�^�͐}2.8�Ɏ�����Ă���20�l�������̂܂ܗp���čs���B
2.2 �ʏ�^SAS�v���O�����̗��� �@��6��(5)�ɗᎦ����Ă���ʏ�^SAS�v���O�������ǂ�ȏ������s���Ă���̂��A���{��Ő�������B�q���g����5���A��6���̊e���ɕ��U���Ă���B
2.3 �ʏ�^SAS�v���O�����̎��s �@��6��(5)�ɗᎦ����Ă���ʏ�^SAS�v���O�����������œ��͂��A���ۂɒP���W�v���s���Ă݂�B���̌��ʂ���6��������F�̌`�����Q�l�ɂ��Ȃ���A����B�̎��⒲���[�Ɏ菑���ŏ������݁A�P���W�v�̌��ʂ����B
2.4 �P���W�v�̗����p �@���K���2.1 (�܂���2.3)�ō쐬�����P���W�v�Ɋ�Â��āA���̂��Ƃɂ��Đ������Ă܂Ƃ߂�B
�@���̏͂���́A�����ɂ���ē���ꂽ�f�[�^����̓I�ɂǂ̂悤�ɓ��v��������̂���������邱�Ƃɂ��悤�B�܂������ɂ���ē���ꂽ�f�[�^�ɂ��čl���Ă݂悤�B�Ⴆ�u�g�D�������̂��߂̏]�ƈ��ӎ������v(�ڍׂɂ��Ă���6���ʼn������)���s���A�l�P�ʂ̎��⒲���[������ł���B��2�͑�5���̐}2.7�ɂ́A���̒����ɂ���ē���ꂽ�̈ꕔ20�l�����f�[�^�Ƃ��ĕ\������Ă��邪�A���܂��̍ŏ���8�l�A���Ȃ킿�g�D�P�ʃR�[�h57�́uE�T�[�r�X���̏����ۑS�T�[�r�X����v�ɂ��āA���ʁA�E��A�E�ʂ�}�ɕ\������Ă���R�[�h�̂܂܂ŕ��ׂ�A�\3.1(A)�̂悤�ȃf�[�^������ꂽ���ƂɂȂ�B����ł͐l�Ԃɂ̓s���Ƃ��Ȃ��̂ŁA���̃J�e�S���[�̌`�ɖ߂��ĕ\������ƕ\3.1(B)�̂悤�ɂȂ�B
�\3.1�@E�T�[�r�X���̏����ۑS�T�[�r�X����̐��ʁA�E��A�E�ʃf�[�^
(A)�R�[�h�\���@�@�@�@�@�@(B)�J�e�S���[�\��
| �l�ԍ� | ���� | �E�� | �E�� |
|---|---|---|---|
| �@1�@ | 1 | 1 | 4 |
| �@2�@ | 1 | 1 | 4 |
| �@3�@ | 1 | 1 | 3 |
| �@4�@ | 1 | 1 | 4 |
| �@5�@ | 1 | 1 | 2 |
| �@6�@ | 1 | 2 | 3 |
| �@7�@ | 1 | 1 | 2 |
| �@8�@ | 1 | 1 | 2 |
| �l�ԍ� | ���� | �E�� | �E�� |
|---|---|---|---|
| 1 | �j | ���� | ��� |
| 2 | �j | ���� | ��� |
| 3 | �j | ���� | �W�� |
| 4 | �j | ���� | ��� |
| 5 | �j | ���� | �ے� |
| 6 | �j | �Z�p | �W�� |
| 7 | �j | ���� | �ے� |
| 8 | �j | ���� | �ے� |
�@�\3.1������ʉ����āAn �l�̃f�[�^�Ƃ��ď����\���A�\3.2�̂悤�ɂȂ�B�����ŁAx, y, z �͂��ꂼ��ϐ�(variable)���邢�͕ϗ�(variate)�ƌĂ��B(�������A���v�̕���ł͈��q���́A�听�����́A���ʕ��͓��̂��đ��ϗʉ��(multivariate analysis)�ƌĂԂ��A�����"�ϐ�"��͂Ƃ͂���Ȃ��̂Œ��ӂ�����B) ����ɑ��āAxi, yi, zi�͊ϑ��l�A����l�ƌĂ��B�ϑ��l�́A�ϐ��Ƌ�ʂ��邽�߂ɓY����t���ĕ\�����Ƃɂ��悤�Bn �̓f�[�^�̃T�C�Y��\���Ă���B
�\3.2�@��ʂ�3�ϐ��� n �l�f�[�^
| �@�@�@ | �@x�@ | �@y�@ | �@z�@ |
|---|---|---|---|
| 1 | x1 | y1 | z1 |
| 2 | x2 | y2 | z2 |
| : | : | : | : |
| i | xi | yi | zi |
| : | : | : | : |
| n | xn | yn | zn |
�@�Ⴆ�A���ʂ����̃f�[�^�A���͂���8�l�͑S�����j���Ȃ̂����A
�@�@�@�j, �j, �j, �j, �j, �j, �j, �j
�̂悤�Ȉ�̕ϐ��̊ϑ��l����Ȃ�f�[�^�Ax1, x2, ... ��1�ϐ��f�[�^���邢��1�����f�[�^(1-dimensional data)�Ƃ�����B����ɑ��āA�Ⴆ�A���ʂƐE�킩��Ȃ�f�[�^�A
�@�@�@(�j, ����), (�j, ����), (�j, ����), (�j, ����), (�j, ����), (�j, �Z�p), (�j, ����), (�j, ����)
�̂悤�ɓ�̕ϐ��̊ϑ��l����Ȃ�f�[�^�A(x1, y1), (x2, y2), ... ��2�ϐ��f�[�^���邢��2�����f�[�^(2-dimensional data)�Ƃ�����B����2�ϐ��̏ꍇ���܂߂āA2�ϐ��ȏ�̊ϑ��l����Ȃ�f�[�^�A�Ⴆ��3�ϐ�����Ȃ�f�[�^�A
�@�@�@(�j, ����, ���), (�j, ����, ���), (�j, ����, �W��), (�j, ����, ���), (�j, ����, �ے�), (�j, �Z�p, �W��), (�j, ����, �ے�), (�j, ����, �ے�)
��ʓI�ɂ́A(x1, y1, z1),(x2, y2, z2),... �Ȃǂ́A���ϐ��f�[�^���邢�͑������f�[�^(multidimensional data)�ƌĂ��B
�@���́A�ʏ퓾���钲���f�[�^�́A���̂悤�Ɋe�ϐ��ɂ��Ă̂��邱�Ƃ�1�ϐ��f�[�^�Ƃ��Ĉ������Ƃ��ł��邵�A�����̕ϐ��̑g�����邱�ƂŁA���ϐ��f�[�^�Ƃ��Ĉ������Ƃ��ł���B1�ϐ��f�[�^�Ƃ��Ĉ����̂ł���A�e�ϐ��P�Ƃł̓����ׂ邱�ƂɂȂ邵�A���ϐ��f�[�^�Ƃ��Ĉ����̂ł���A�ϐ��Ԃ̊W�ׂ邱�ƂɂȂ邪�A������ɂ���A1�ϐ����邢�͑��ϐ��̃f�[�^���E�v�āA�W�{�����Ȃ�ΕW�{�́A�S�������Ȃ�Ε�W�c�̏W�c�Ƃ��Ă̓������L�q���邱�Ƃ��L�q���v�w(descriptive statistics)�̖����ł���B�������A�L�q���v�w�Ƃ������O�����Ă��邩�ǂ����ɂ�����炸�A�f�[�^���E�v�邱�Ƃ͏d�v�Ȃ��Ƃł���B
�@���̏͂ł́A1�ϐ��f�[�^�̐����E�v��ɂ��Ď�舵�����A�f�[�^���玖����T��A�m�邽�߂ɂ͂��̃X�e�b�v�͌������Ȃ��B���v�I�ɕ��͂�����ۂɂ́A��������Ƃ����Ȃ荂�x�Ȏ�@�ɑ��肪���ł��邪�A����ꂪ�u���́v�ƌĂ�ł���ߒ��́A���̃f�[�^�̐����E�v��A����1�ϐ��̃f�[�^�̐����E�v���������Ƃ��Ă����Ȃ��ƁA�����Ζ��Ӗ��ɂȂ��Ă��܂����Ƃ�����B�������A���̃f�[�^�̐����E�v��̉ߒ����̂��A
�@��1���ŏq�ׂ��悤�ɁA���`�ړx�A�����ړx�ɂ��ƂÂ��f�[�^�̂��Ƃ����I(�萫�I)�f�[�^(qualitative data)�Ƃ����A�Ԋu�ړx�A�䗦�ړx�ɂ��ƂÂ��f�[�^�̂��Ƃ�ʓI(��ʓI)�f�[�^(quantitative data)�Ƃ����B���I�f�[�^�A�ʓI�f�[�^�̋�ʂƂ���Ӗ��ł͍������ꂪ���Ȃ��̂ɁA���U�ϐ��ƘA���ϐ��̋�ʂ�����̂ŁA�ꉞ�������Ă������B���U(discrete)�ϐ��Ƃ́A�Ƃ肤��l�����X�Z�A�܂�L���܂��͉Z�����A�Ⴆ�A�Ƃ肤��l�̏W�����A�����A�L�����̕ϐ��ł���B����ɑ��āA�A��(continuous)�ϐ��Ƃ́A�Ƃ肤��l���Z�ł͂Ȃ��A�Ⴆ�A�Ƃ肤��l�̏W���������S�̂ł���悤�ȕϐ��ł���B���́A�����ł����u�A���v�͒ʏ�̐��w�I�Ӗ��Ŏg���Ă���̂ł͂Ȃ��A�u���U�v�ƑΔ䂵�Ďg�p����Ă���ƍl���������悢�B
�@���U�ϐ��ƘA���ϐ��̋�ʂ͐������v�w�A�m���_�̏�ł͈Ӗ��̂���敪�����A���ۂ̃f�[�^���W�A���v������́A�����ɋ�ʂ��邱�Ƃɂ͂��܂�Ӗ����Ȃ��B�Ȃ��Ȃ�A�܂��A���ۂ̊ϑ��l�͐��m�ɂ͏�ɗ��U�I������ł���B�����̏�ł͘A���ϐ��ł����Ă��A���̊ϑ��l�͑���@��̐��x�̌��E�A���̖͂ړI�ɂ��A�K���Ȍ����̗L�������Ɋۂ߂��A���U�I�ƂȂ�̂ł���B�������A�t�ɁA���Ƃ������̏�ł͗��U�ϐ��̏ꍇ�ł��A�Ƃ肤��l�������Ƃ��ɂ́A�u�����̓_���v�̂悤�ɁA�A���ϐ��Ƃ݂Ȃ��ď������邱�Ƃ������̂ł���B
�@�����ŁA�{���ł́A���I�f�[�^�ƗʓI�f�[�^�̊�{�I�ȋ�ʂɒ��ӂ��Ȃ���A������i�߂Ă������Ƃɂ��悤�B
�@���v�f�[�^�����Ƃ͌��ǁA���ɐ}�E�\�ɂ܂Ƃ߂邱�Ƃł���B�ƌ������猾���߂����낤���B�����Ƃ��ẮA���v�f�[�^�̖{�������Ă�������͂����Ɉ����o���}�E�\�ɂ�鐮�����o����̂ł���A����ȏ�̍��x�ȓ��v��@�͕s�v�Ȃ��̂Ɏv����B���Ȃ��Ƃ��A�}�E�\�ɂ܂Ƃ߂āA�S�̂��L�q������ŁA�͂��߂Ă��ꂩ���̏����A���͂ɐi�ނ��Ƃ��ł���Ƃ������Ƃ��̂ɖ����Ă����ׂ��ł��낤�B���̏͂ł��ꂩ��������Ă������A���ρA���U�Ƃ��������ɂ悭�p�������{�I�ȓ��v�ʂł���A���z�̌`���Ȃ߂炩�Ő����Ă�������A�p���邱�Ƃ��\�ɂȂ�̂ł���B
�@�\�ɂ��L�q�́A���I�f�[�^�ɑ��Ă��ʓI�f�[�^�ɑ��Ă��s���邪�A�ʓI�f�[�^�ł́A�܂��f�[�^�̒l���������̒i�K�ɕ������u�K���v(class)�ƌĂ����̂�ݒ肷��B���̊K���͎��I�f�[�^�́u�J�e�S���[�v�ɑ���������̂ł���A���̂��ߌ`���I�ɂ́A���I�f�[�^���ʓI�f�[�^�����̓x�����z�\(frequency table)�A�ݐϓx�����z�\(cumulative frequency table)�͓������̂ɂȂ�B�����ŁA�x���Ƃ́A���Y�J�e�S���[�������͊K���ɊY������I�u�U�[�ׁ[�V���������v���������̂ł���B�ݐϓx���Ƃ́A�ʓI�f�[�^�̏ꍇ�ɂ͓x�������̊K�����珇�ɐςݏグ���Ƃ��̓x���ł���B���I�f�[�^�̏ꍇ�ɂ́A�J�e�S���[�̕���ł��鏇�ɐςݏグ���Ƃ��̓x���ɂȂ�B
�@���ہA���I�f�[�^�̕\�A�ʓI�f�[�^�̕\�́A�Ⴆ�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̃f�[�^��p����ƁA���ꂼ��\3.3(A)(B)�̂悤�ɂȂ�A�`���I�ɂ͓������̂ƂȂ�B
�\3.3�@�x�����z�\�E�ݐϓx�����z�\�̗�
(A)���I�f�[�^(����)�̓x�����z�\�E�ݐϓx�����z�\
| �J�e�S���[ | �@�x���@ | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|
| �j | 765 | 87.2 | 765 | 87.2 |
| �� | 112 | 12.8 | 877 | 100.0 |
| �v | 877 | 100.0 | - | - |
(B)�ʓI�f�[�^�i�N��j�̓x�����z�\�E�ݐϓx�����z�\
| �K�� | �@�x���@ | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|
| 20�`24�� | 60 | 6.7 | 60 | 6.7 |
| 25�`29�� | 169 | 18.8 | 229 | 25.5 |
| 30�`34�� | 175 | 19.5 | 404 | 45.0 |
| 35�`39�� | 153 | 17.1 | 557 | 62.1 |
| 40�`44�� | 159 | 17.7 | 716 | 79.8 |
| 45�`49�� | 99 | 11.0 | 815 | 90.9 |
| 50�`54�� | 62 | 6.9 | 877 | 97.8 |
| 55�`60�� | 20 | 2.2 | 897 | 100.0 |
| �@�@�v�@�@ | 897 | 100.0 | - | - |
�@�\3.3�̒��̊e���x�����z�A���Γx�����z�A�ݐϓx�����z�A�ݐϑ��Γx�����z�Ƃ������Ƃ�����B�u���v�Ƃ��Ă���̂́A�S�̂ɑ��鑊�ΓI�ȕS������\���Ă��邩��ł���B���Γx���́A�W�c�̑傫��n���قȂ镡���̏W�c�̕��z���r����Ƃ��ɗL���ł���BSAS���g���ďW�v���������ꍇ�ɂ��A����������{�I�ȓx��(frequency)�A���Γx�� (relative frequency)�A�ݐϓx��(cumulative frequency)�A�ݐϑ��Γx��(relative cumulative frequency)�͏o�͂���邱�ƂɂȂ�B������ɂ���A(A)(B)���҂��`���I�ɂ͓������̂ł��邱�Ƃ��킩�邾�낤�B���I�f�[�^�̕\�A�ʓI�f�[�^�̕\������ʓI�ɑΏƂ��Ď����A�\3.4�̂悤�ɂȂ�B
�\3.4�@�x�����z�\�E�ݐϓx�����z�\
(A)���I�f�[�^
| �J�e�S���[ | �@�x���@ | �@���Γx���@ | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|
| A1 | f1 | f1 /n�~100 | F1 | F1 /n�~100 |
| A2 | f2 | f2 /n�~100 | F2 | F2 /n�~100 |
| : | : | : | : | : |
| Ai | fi | fi /n�~100 | Fi | Fi /n�~100 |
| : | : | : | : | : |
| Ak | fk | fk /n�~100 | Fk | Fk /n�~100 |
(B)�ʓI�f�[�^
| �@�K�@���@ | �@�x���@ | �@���Γx���@ | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|
| a1�`b1 | f1 | f1 /n�~100 | F1 | F1 /n�~100 |
| a2�`b2 | f2 | f2 /n�~100 | F2 | F2 /n�~100 |
| : | : | : | : | : |
| ai�`bi | fi | fi /n�~100 | Fi | Fi /n�~100 |
| : | : | : | : | : |
| ak�`bk | fk | fk /n�~100 | Fk | Fk /n�~100 |
�@���������\������킩��悤�ɁA�ݐϓx�����z�͓x�����z����ȒP�Ɍv�Z�ł��邵�A�t�ɗݐϓx�����z����x�����z���Z�o���邱�Ƃ��ł���B���̂��Ƃ́A�x�����z�Ɨݐϓx�����z�Ƃ����������̏����܂�ł��邱�Ƃ��Ӗ����Ă���B���������āA�ǂ��炩����������Ώ\���Ȃ킯�����A�ʏ�́A�x������ё��Γx���̕��z���������悢�B�����ł͐G��Ȃ����A�ݐϓx������їݐϑ��Γx���͂�����ȗp�r�ɗp������B
�@�����ŁA�u���z�v�Ƃ����p��̎g�p�ɂ��Ă�⒍�ӂ��q�ׂĂ����ƁA��W�c�̕��z�̌`�𐳋K���z�Ȃǂŕ\�����邱�Ƃ����邪�A����͑��Γx�����z���m�����z�Ɍ����Ăėp����̂ł���B���̏ꍇ�A�u��W�c���z�v�͐��m�ɂ͑��Γx�����z�̂��Ƃł����āA�m�����z���Ӗ�������̂ł͂Ȃ��B�u�m���v���z�́A�W�{���o�A���m�ɂ͖���ג��o�Ƃ����m���I���u��ʂ��āA�W�{���z�ɂ͂��߂Č����̂ł����āA��W�c�ɂ͘_���I�ɂ͑��݂��Ȃ��T�O�ł���B���Ȃ݂ɁA���v�w�ł����u�W�{���z�v�Ƃ͕W�{�ɂ����镽�ςȂǂ̓��v�ʂ̕��z�̂��Ƃł����āA����͊m�����z�ł���B�W�{�ɂ�����L�q���v�Ƃ��Ă̓x�����z�̂��Ƃł͂Ȃ��̂ŁA���̓_�ɂ����ӂ�����B
�@�x�����z�\�A���Γx�����z�\�A�ݐϕ��z�\�A�ݐϑ��Γx�����z�\�����߂邱�Ƃ́ASAS���g���ΊȒP�ł���B�P���W�v�̂Ƃ��Ɠ��l��FREQ�v���V�W�����g���悢�̂ł���B���ہA���I�f�[�^�ł���A�P���W�v�Ƃ͓x�����z�\����邱�ƂƓ������ƂɂȂ�B��2���ō쐬�����i�vSAS�f�[�^�E�Z�b�g(PC��SAS�̃v���O������ł�JPC.SSD�ACMS��SAS�̃v���O������ł�JPC SAVE)�𗘗p����A�x�����z�\�쐬�̂��߂�SAS�v���O�����͂킸���ɐ��s�ōςށB
�@����ɂ�2�ʂ�̕��@�������āA�܂��ŏ��̕��@�Ƃ��ẮASAS�v���O�����̊�{�`�ł���DATA�X�e�b�v��PROC�X�e�b�v��2�X�e�b�v�\���ɂ��������@�ŁA���̂Ƃ��͎��̂悤�ȃv���O�����ɂȂ�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; DATA libname.�i�vSAS�f�[�^�E�Z�b�g���{��; SET libname.�i�vSAS�f�[�^�E�Z�b�g���{��; PROC FREQ; TABLES �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; DATA SAVE.JPC; �@SET SAVE.JPC; PROC FREQ; �@�@�@TABLES I2; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
DATA �i�vSAS�f�[�^�E�Z�b�g��; SET �i�vSAS�f�[�^�E�Z�b�g��; PROC FREQ; TABLES �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
DATA SAVE.JPC; �@SET SAVE.JPC; PROC FREQ; �@�@�@TABLES I2; �@�@�@OPTIONS NOCENTER; RUN; |
�@CMS��SAS�̃v���O�����́A�`���I�ɂ�PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�B���̃v���O�����̂悤��DATA�X�e�b�v������ƁA���e�I�ɂ͉��̕ύX���Ȃ��S�������i�vSAS�f�[�^�E�Z�b�g�������I�ɂ܂���蒼���Ă��邱�ƂɂȂ�̂ŁA���̕��������Ԃ�������B���C���t���[���ł͋C�ɂȂ�Ȃ����A�p�[�\�i���E�R���s���[�^�ł́A�M�҂̎����ł�DATA�X�e�b�v�ɖ�2���قǂ�����BPROC�X�e�b�v�ɂ�20�b����������Ȃ��̂ŁA���Ԃ̖��ʂƂ����Ȃ����Ƃ��Ȃ��B
�@�����ŁA������̕��@�Ƃ��ẮADATA�X�e�b�v���Ȃ����āAPROC�X�e�b�v�����ɂ��āA���ډi�vSAS�f�[�^�E�Z�b�g���Q�Ƃ�������@������B���̕��@�ł́APROC�X�e�b�v�ɂ����鎞�Ԃ����ōςނ̂ŁA20�b�ȓ��ɏ������\�ł���B�܂�DATA�X�e�b�v���Ȃ��������A�v���O�������ȒP�ɂ��邱�Ƃ��ł���B����ɂ́A���̂悤��PROC FREQ����DATA=�I�v�V�����ʼni�vSAS�f�[�^�E�Z�b�g�����w�肵�Ă��܂��̂ł���B������̕����ł́ADATA�X�e�b�v�͕s�v�ɂȂ�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC FREQ DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; TABLES �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I2; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC FREQ DATA=�i�vSAS�f�[�^�E�Z�b�g��; TABLES �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I2; �@�@�@OPTIONS NOCENTER; RUN; |
�@�����قǂƓ��l�ɁACMS��SAS�̃v���O�����́A�`���I�ɂ�PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�B�{���ł͂���ȍ~�A���ɒf��Ȃ�����A���̌�҂̕�����PROC����DATA=�I�v�V�����Ŏw�肷����@�ł̂݁ASAS�v���O�����̉�������邱�Ƃɂ��悤�B
�@�v���O������̒��̕ϐ�I2�́u�g�D�������̂��߂̏]�ƈ��ӎ������v(�ڍׂ���6��)�ł́A�N���\���ϐ��ł���B�ϐ�I2�ɂ��ẮA����܂ł̒����o���Ǝ��O�m������A���ɒ������Ƀv���R�[�f�B���O���Ă���̂ŁA���́A�P���W�v�����߂邱�ƂŁA���N��K�w�ʂ̓x�����z�����߂邱�Ƃ��o����B��������q����悤�ɁA�ʏ�͂ǂ̂悤�ȊK����ݒ肷��̂��ɂ��ẮA���̓x�����z�\���쐬���Ȃ��玎�s������d�˂Ĕ[���̂����悤�ȊK����ݒ肵�Ȃ��Ă͂Ȃ�Ȃ��B�����Ŏ��������ނ́A������������܂ł̎��s����̈ꐬ�ʂł���ƍl���Ăق����B
�@����SAS�v���O���������s������ƁA�ǂ���̃v���O������ł����̂悤�ȏW�v���ʂ��[���̉�ʂɕ\������邱�ƂɂȂ�B
�}3.1�@SAS�ŋ��߂��x�����z�\
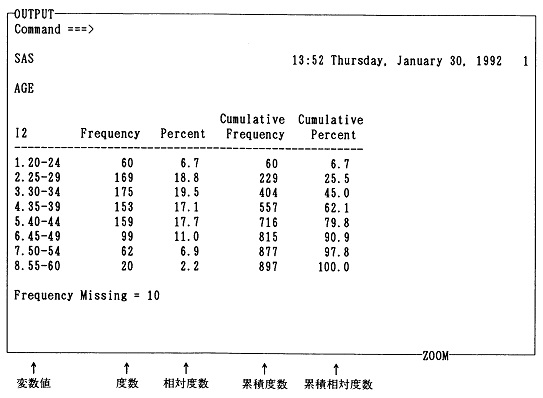
�@���́A���̐}3.1�̏W�v���ʂ���A���ɒ����\3.3(B)���쐬����Ă���B�����ŁA�}3.1�Ɏ�������ʂ̈�ԉ��̍s�ɂ�
�@�@�@Frequency Missing = 10
�Ƃ��邪�A����͔N���\���ϐ�I2�Ō����l�ƂȂ��Ă���l��10�l�������Ƃ������Ă���B�S�̂�1.1% (��10/(897+10))���x�������l���������ƂɂȂ邪�A���̒��x�̒ᐅ���ɗ}�����Ă���̂ł���A�����f�[�^�Ƃ��Ă͗ǍD�Ȃ��̂��Ƃ����邾�낤�B
�@�\�ŋL�q����ꍇ�̓x�����z�\�A�ݐϓx�����z�\�ɑΉ����āA�ʓI�f�[�^�A���I�f�[�^�Ƃ��ɁA���ꂼ��2��ނ̐}�ŋL�q���邱�Ƃ��ł���B
�@���̏ꍇ�ɂ́A�x�����z�\�ɑΉ����ăq�X�g�O�����A�ݐϑ��Ε��z�\�ɑΉ����ėݐϓx�����p�`���`�����B
�@�q�X�g�O�����Ɨݐϓx�����p�`�̗�Ƃ��āA�\3.3(B) (���邢�͐}3.1)�̓x�����g���ĕ`���Ă݂�ƁA�}3.2�̂悤�ɂȂ�B���̂����A�ݐϓx�����p�`�̃O���t�ł́A�����̂��߂Ƀq�X�g�O�����̒����d�ˍ��킹�Ď�����Ă��邪�A�ݐϓx�����p�`�͐܂���̕��������Ȃ̂ŁA���ӂ��Ăق����B
�}3.2�@�q�X�g�O�����Ɨݐϓx�����p�`
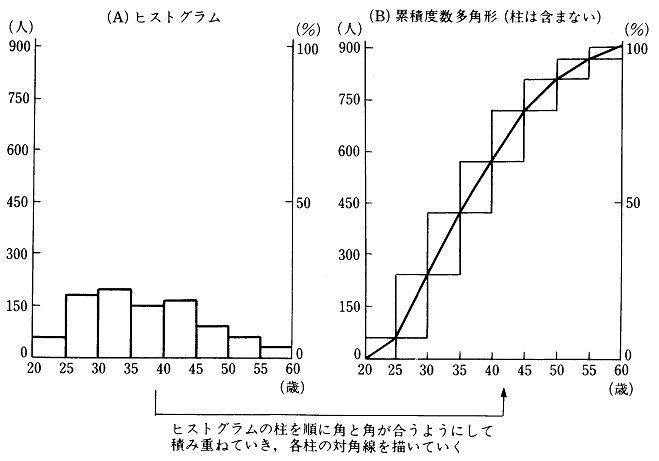
�@�Ƃ���ŁA���̗�ł́A�N���60�܂łɂȂ��Ă��邪�A��Ƃ̂悤�ɒ�N���̂���Ƃ���͕ʂƂ��āA��ʓI�ɂ͔N��̂悤�ȕϐ��̍Ō�̊K���́A�I�[�v���E�G���h�̊K���A�܂������킩��Ȃ��K���ƂȂ��Ă��邱�Ƃ������B���������I�[�v���E�G���h�̊K���̏��u�����͂��₵���Ȃ��Ă��܂��B���m�ɐ}��`�����Ƃ��o���Ȃ��̂ł���B�q�X�g�O�����̏ꍇ�ɂ́A�����ʐς������߂ɂ��āA�ڕ��ʂŋL�����邵���Ȃ����A�ݐϓx�����p�`�̏ꍇ�ɂ́A100%����≺�̂Ƃ���ɖڕ��ʂŐ������Ԃ����Ȃ��̂ł���B���������āA�q�X�g�O������ݐϓx�����p�`�𐳊m�ɕ`�����Ƃ��l���Ă���̂ł���A�I�[�v���E�G���h�̊K���͕s�p�ӂɍ��ׂ��ł͂Ȃ��B�������̂ł���A���̊K���ł̃f�[�^�̕��ϒl�A�ŏ��l�܂��͍ő�l�𒍋L����S�������ق����B
�@���̏ꍇ�ɂ́A�x�����z�\�ɑΉ����Ė_�O���t�A�ݐϑ��Ε��z�\�ɑΉ����ėݐϓx���܂�����l������B
�@�����������̂ɂ͗ʓI�f�[�^�ŁA�K�����J�e�S���[�Ƃ��Ĉ����ꍇ���܂߂���B���́A�{���ň����Ă���悤�ȕ���̓��v�ł́A�q�X�g�O������ݐϓx�����p�`��`�����Ƃ͂قƂ�ǂȂ��B�Ƃ��������ASAS�Ȃǂ̓��v�p�b�P�[�W���g���ďW�v����ꍇ�ɂ́A�ʓI�f�[�^�ł����Ă��A���ǂ͊K�����J�e�S���[�Ƃ��Ĉ����āA�����������I�f�[�^�ł��邩�̂悤�ɖ_�O���t��`�����邱�ƂɂȂ��Ă��܂��B�Ⴆ�A���̗�́A�}3.2�̃q�X�g�O�����A�ݐϓx�����p�`���A�K�����J�e�S���[�Ƃ��āA(����)�_�O���t�A�ݐϓx���܂����`�������̂ł���B
�}3.3�@�_�O���t�Ɨݐϓx���܂��
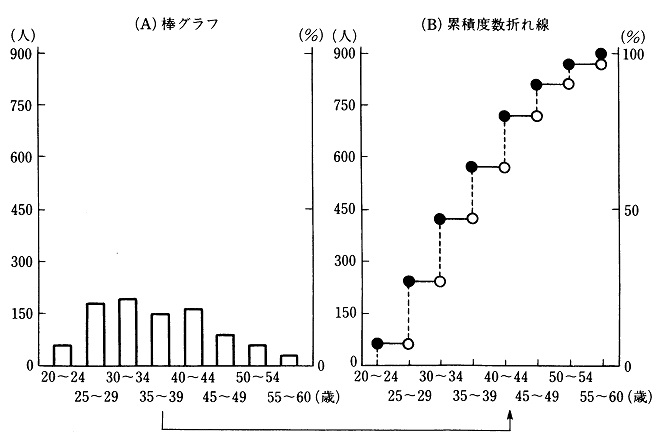
�@�_�O���t���쐬���邱�Ƃ́ASAS���g���ΊȒP�ł���BCHART�v���V�W�����g���悢�B��3�͂ō쐬�����i�vSAS�f�[�^�Z�b�g(��ł�JPC91 SAVE)��PROC����DATA=�I�v�V�����Ŏw�肷��A�_�O���t�쐬�̂��߂�SAS�v���O�����͂킸����3�`4�s�ōςށB
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC CHART DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; HBAR �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC CHART DATA=SAVE.JPC; �@�@�@HBAR I2; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC CHART DATA=�i�vSAS�f�[�^�E�Z�b�g��; HBAR �ϐ����̕���;�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
PROC CHART DATA=SAVE.JPC; �@�@�@HBAR I2; �@�@�@OPTIONS NOCENTER; RUN; |
�@����������قǂƓ��l�ɁACMS��SAS�̃v���O�����́A�`���I�ɂ�PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�B�x�����z�\�����߂�v���O�����Ɣ�r���Ă��A�L�[���[�h��FREQ��TABLES���A���ꂼ��CHART��HBAR�ɒu���������Ă��邾���ł���B
�@�v���O������̒��̕ϐ�I2�͊��ɏq�ׂ��悤�ɁA�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̗�ł͔N���\���ϐ��ł���B����ɂ���āA�N��̓x�����z�����߂邱�Ƃ��o����B����SAS�v���O����������s������ƁAPC��SAS�ł�20�b��Ő}3.4�̂悤�ȏW�v���ʂ���ʂɕ\������邱�ƂɂȂ�B
�}3.4�@SAS�ŋ��߂������_�O���t
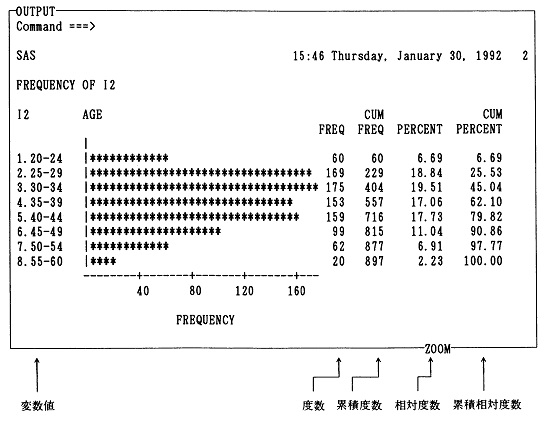
�@�v���O�������̃L�[���[�h"HBAR"��"VBAR"�ɕς���ƁA�}3.4�ɗᎦ�����悤�Ȑ����_�O���t�̑���ɁA�}3.5�ɗᎦ�����悤�Ȑ����_�O���t���\������邱�ƂɂȂ�B�������A�}3.5�����Ă��킩��悤�ɁA�����_�O���t�ł͓x���A�ݐϓx���A���Γx���A�ݐϑ��Γx���͕\�����ꂸ�A�����_�O���t�݂̂̕\���ƂȂ�B
�}3.5�@SAS�ŋ��߂������_�O���t
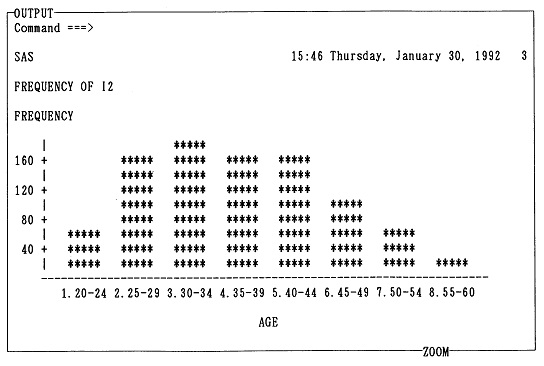
�@�K���̐ݒ�ɂ́A����������ǂ��Ƃ����悤�Ȉ�ʓI�ȃ��[���͑��݂��Ȃ��B�ނ���A���s������J��Ԃ��Ȃ��猈�߂Ă����ׂ����Ƃ����������悢���낤�B�������A���s����Ƃ͂����Ă��A���Ƃł��̂͑�ςł���B�W�v�͂��Ă����Ă��A���x���}�\����蒼���̂́A���ꂾ���ł���ςȍ�ƗʂƂȂ�B���������āA���p�I�ȈӖ��ŁA���x���C�̍ςނ܂Ŏ��s���낪�ł���̂́ASAS���̓��v�p�b�P�[�W�̂������Ƃ������ƂɂȂ�B���̌��ʂƂ��āA�Ȃ߂炩�Ȑ������`�̕��z�̃q�X�g�O������_�O���t��������A�ꉞ�������Ď��s������I������킯�ł���B�������A�Ȃ߂炩�Ő������`�ł��邱�Ƃ��A�ǂ��K���ݒ�̗B��̊�ł͂Ȃ��B����K���ݒ肪�ǂ����̂ł��邩�ǂ����́A���v���������ĕ��͂��鑤�̈Ӑ}�ɑ傫���ˑ����Ă���̂ł���B���̂��Ƃ́A��q�̗��������ōl���Ă݂�Ƃ悭�킩��B
�@�������A���̂悤�ȃ|�C���g�́A�ꉞ�A���̕Ћ��ɒu���Ē��ڂ��Ă݂�Ɩ��ɗ��̂ŁA�����l����ۂɂ��Q�l�ɂ��Ăق����B
�@�����ŁA�|�C���g2�̃X�^�[�W�F�X�̌o�������̒��� log �͏�p�ΐ� log10 �̂��Ƃł���B���̌����ɂ��A�܂��f�[�^��1�̏ꍇ�ł��K���͈�͕K�v�ł���B����ɁA�f�[�^�̃T�C�Yn��2�{�ɂȂ邲�ƂɊK���̌�k������₵�������悢�Ƃ����̂ł���B���ۂɂ������̃f�[�^�E�T�C�Y�ɂ��āA���̌�����p���ĊK���̌����v�Z���Ă݂�ƁA�\3.5�̂悤�ɂȂ�̂ŁA�Q�l�ɂ���Ƃ悢�B
�\3.5�@�f�[�^�̃T�C�Y�ƊK���̌�
| �f�[�^�̃T�C�Y(n) | 10 | 20 | 50 | 100 | 200 | 500 | 1,000 | 2,000 | 5,000 | 10,000 |
|---|---|---|---|---|---|---|---|---|---|---|
| �K���̌�(k) | 4.32 | 5.32 | 6.64 | 7.64 | 8.64 | 9.96 | 10.96 | 11.96 | 13.28 | 14.28 |
���)�@���̃f�[�^�́A�^���A�����s�̂��鏬���X�̂����A100�������������I�ɒ��o���āA�����ɂ�����^�i�̍ɗ�(�P�ʂ͌�)�ׂ����̂ł���(��, 1973, p.11)�B�x�����z��}�\�����Ă݂�B�������SAS�����g�킸�Ɏ�v�Z�ł���Ă��܂�Ȃ��B���̓x�����z����ǂ�Ȃ��Ƃ������邩�B
| 21 | 142 | 0 | 282 | 187 | �@ 100 | 0 | 0 | 225 | 42 |
| 72 | 159 | 33 | 21 | 61 | 593 | 0 | 47 | 97 | 0 |
| 0 | 4 | 192 | 0 | 17 | 75 | 133 | 125 | 13 | 163 |
| 122 | 30 | 0 | 263 | 27 | 186 | 23 | 41 | 18 | 44 |
| 0 | 8 | 12 | 4 | 47 | 20 | 0 | 16 | 91 | 20 |
| 0 | 18 | 6 | 0 | 25 | 29 | 178 | 8 | 110 | 0 |
| 62 | 0 | 98 | 0 | 55 | 0 | 0 | 43 | 75 | 61 |
| 14 | 0 | 63 | 0 | 25 | 0 | 27 | 12 | 561 | 62 |
| 14 | 20 | 34 | 64 | 43 | 90 | 169 | 4 | 81 | 44 |
| 85 | 4 | 10 | 19 | 0 | 35 | 39 | 28 | 0 | 0 |
�@�����������ɂ͂�����̐����Ƃ������̂͂Ȃ��B�|�C���g2�ɂ��ẮAn=100 �ł��邩��A�X�^�[�W�F�X�̌�������K���̐���7�`8�Ƃ������Ƃ���ł���B���̓|�C���g1�ŁA����ɂ��ē�̉���l���Ă݂悤�B
�@�K���̋�ԂԊu�ɂƂ����ꍇ�A���̂悤�ȓx�����z�\�A�_�O���t���`����B�f�[�^���ꌩ���āA0���������Ƃ��킩��̂ŁA�u0�v�����ň�̊K���ɂ��Ă���B�Ȃ��_�O���t�͓x�����z�ƑΏƂ����邽�߂ɁA�����_�O���t�ɂ��Ă���B
�}3.6�@��1
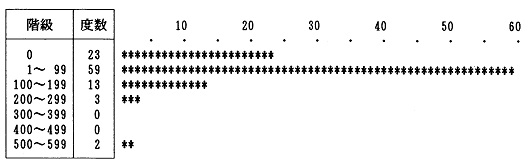
�@���̖_�O���t����A��r�I���ꂢ�ɕ��z���Ă���l�q���킩��B�������A���́A���������f�[�^�ɑ��āA���̉�̂悤�ɁA���Ԋu�������`���I�ɓK�p����ƁA�ϑ��l���Е��̒[�̂������������ɋ�̓I�ɂ�0�`199�ɏW�����āA�W�������̏�����Ă��܂����ƂɂȂ�B���̂��Ƃ́A���̉�2�Ɣ�r����Ƃ悭�킩��B
�@�K���̋�Ԃ�ΐ��̈Ӗ��œ��Ԋu�ɂƂ����ꍇ�B����͑ΐ����Ƃ�A
�@�@�@log a�b��log a�{log b
�@�@�@log a�bn��log a�{n log b
�Ƃ������������邱�Ƃ���A�܂�b�{���Ƃɑΐ��̈Ӗ��œ��Ԋu�ɂȂ��Ă���ƍl����̂ł���B�X�^�[�W�F�X�̌�������K���̐���7�`8�Ƃ������Ƃ�z�����āA����2�{���Ƃɋ���ĊK��������Ă݂�Ǝ��̂悤�ɂȂ�B
�}3.7�@��1
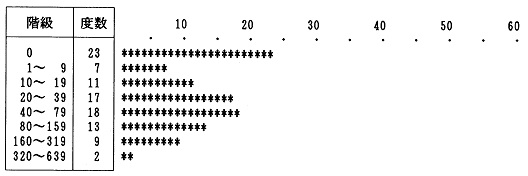
�@�O�̂��߁A�e�K���̋��̒l�̑ΐ����Ƃ�Ǝ��̂悤�ɂȂ��Ă���B
�@�@�@log 10
�@�@�@log 20=log 10+log 2
�@�@�@log 40=log 10+2 log 2
�@�@�@log 80=log 10+3 log 2
�@�@�@log 160=log 10+4 log 2
�@�@�@log 320=log 10+5 log 2
�@�@�@log 640=log 10+6 log 2
�@��������ƁA�u0�v�Ƃ����K���������āA���ꂢ�ȕ��z�����Ă��邱�Ƃ��킩��B���̂悤�ȍl�����́A�]�ƈ��K�͂ɑ傫�ȈႢ�̂����Ƃ̏W�c�ɂ��āA�]�ƈ��K�͕ʊ�Ɛ��̓x�����z�ׂ�悤�ȏꍇ�ɂ������悤�ɂ��Ă͂܂�B�Ⴆ�Ώ]�ƈ��K��10�l�̊�ƂɂƂ��ď]�ƈ���10�l��������Ƃ������Ƃ͑�ςȂ��Ƃł���B�������A�]�ƈ��K��10,000�l�̊�Ƃŏ]�ƈ���10�l�������邱�Ƃ͂��܂���ɂ͂Ȃ�Ȃ��B�Ȃ��Ȃ�A�O�҂ł͂�����10�l�ł��]�ƈ��K�͔͂{���������͏��ł��Ӗ����Ă���̂ɁA��҂ł�10�l�ł�0.1���ɂ����Ȃ炸�A���̒��x�̏]�ƈ����̕ϓ��͓���I�ɋN���Ă���\��������B���̂悤�ɁA��ΐ��ł̍������A�ނ��둊�ΓI�Ȕ䗦�ɈӖ�������ƍl������ꍇ�ɂ́A�������䗦���������Ԋu�ɂȂ�悤�ɂ��������悢�B�܂�A�ΐ��̈Ӗ��ł̓��Ԋu�ł���B(�����K���3.1)
�@�Ƃ���ŁA���̉�2�ł́A�K���u0�v�ɏW���������z�̎R�ƁA�K���u40�`79�v���s�[�N�Ƃ������ꂢ�ȕ��z�̎R�̓�̎R�̂��邱�Ƃ��킩��B���̂悤�ɁA���z�̕�������ꍇ�ɂ́A�S�������̈قȂ镡���̕�W�c����̕W�{���������Ă���\��������B���������ꍇ�ɂ́A�w��(stratification)�ɂ���āA�K�ɃO���[�v������ƁA���ꂼ��̃O���[�v�ŁA��̒P���ȕ��z(�P��^;unimodal)������邱�Ƃ������B
�@���̏ꍇ�����̍�Ƃ��K�v��������Ȃ��B���Ȃ��Ƃ��A�u0�v�Ƃ����l�ُ͈�l�ŁA�������ʂȗ��R������͂��ł���B�����炭�A�u�^�i�̍ɗʁv�����Ƃ͂������̂́A���ۂɂ́A���܂��ܒ������ɍɂ�������Ă��āA�ɗʂ�0�������Ƃ��������X�͂��������ŁA�ނ��낻�̑����͂����ƍP��I��0�A�܂�A�����������Y���i���܂�������舵��Ȃ������X��������������̂ł��낤�B�����A���Y���i�������Ă��鏬���X�ł́A���̋K�͓��ōɗʂɂ�������܂�邽�߂ɁA���ꂢ�ȕ��z�����ꂽ���̂Ǝv����B���Y���i���ŏ�����܂���������ɂ��Ă��Ȃ������X��������������Ƃ������Ǝ��̂��A���̏��i�̔̔��S���҂ɂƂ��Ă͏d�v���L�p�ȏ��ƂȂ�ł��낤�B�����Ƃ��A���������L�p�ȏ����A��2�̂悤�ɐ�����������킩�������̂ŁA��1�̂悤�ɐ������Ă��ẮA�C�t����邱�Ƃ��Ȃ��������낤���c�c�B
�@�O�߂̗��̂悤�ɁA�S�������̈قȂ镡���̕�W�c����̕W�{���������Ă���悤�ȏꍇ�ɂ́A������u���ρv�̂悤�ȑ�\�l�ɁA��\�l�Ƃ��Ă̈Ӗ��͂قƂ�ǂȂ��Ƃ������Ƃ͂������킩�肾�낤�B���ꂩ��A���̐߂ň������ρA���U�͒P��^�̕��z��v��ۂɗp������ׂ����̂ł���B
�@�ʏ�A���ςƂ����ΎZ�p����(arithmetic mean)�̂��ƂɂȂ邪�A�Z�p���ς��v�Z���邱�Ƃ́A���v�w��m��Ȃ��l�ł��s���������ʂ̑���ł���Ƃ�����B
�@�T�C�Yn�̃f�[�^x1, x2, ..., xn�̕���x��
�@�@�@x��(x1+x2+���+xn)/n��(1/n)��i=1n xi
���ς͕ϐ�x�̋L���̏�ɉ��_��t����x (�ux�o�[�v�܂��́u�o�[x�v�Ɠǂ�)�ƕ\�L����̂�����ƂȂ��Ă���B
�@�C�ӂ̒萔a, b, c�ɑ��āAax+by+c �̎Z�p���ς��l����ƁA
�@�@�@ax+by+c��(1/n)��i=1n(axi+byi+c)��(a/n)��xi�{(b/n)��yi�{(1/n)nc��ax+by+c
�܂�A�Z�p���ς͎��̂悤�Ȑ���������B
�@�@�@ax+by+c��ax+by+c
���������āA���ϒl���g�������Z�́u�펯�I�v�ɍs�����Ƃ��o����B
�@���R�Ƃ����Γ��R�̂��Ƃł��邪�A���ς͎��ۂɂ͊ϑ�����Ă��Ȃ��l�ɂȂ邱�Ƃ������B���ɗ��U�^�f�[�^�̏ꍇ�ɂ́A�����������肦�Ȃ��l�ɂȂ邱�Ƃ������B
�@�܂� xi-x, i=1, ..., n �ς���̕��ƌĂԂ��A���̘a�͎��Ɏ����悤��0�ɂȂ�B
�@�@�@��i=1n(xi-x)����xi-��x��nx-nx��0
�̐����̈Ӗ�����Ƃ���́A���Ɋe�ϑ��l�ɏd��1�̕��������蓖�āA�������ɂԂ牺�����Ƃ��ɁA���ς̉��̃��[�����g��0�ɂȂ�Ƃ������Ƃł���B�܂�A���ς̏��Ɏx�_������A���̓V���͂荇�����ƂɂȂ�B���̂��Ƃ́A���ς͑S�f�[�^�́u�d�S�v�ɓ���Ƃ������Ƃ��Ӗ����Ă���B���������āA�S�f�[�^�́u���S�v�ɓ�����ƍl����ƌ�����邱�Ƃ�����B
�@�Ⴆ�A10�Ђ��璆�ԊǗ��E1�l���̌v10�l����Ȃ�O���[�v�ŁA�u�����̒��ڂ̕����̐��v�ɂ��Ē��ׂāA�V���Ő}�����Ă݂�ƁA�}3.8�̂悤�Ȍ��ʂɂȂ����Ƃ��悤�B���{�̊�Ƃł́A�|�X�g�s������A���ڂ̕������̏��Ȃ����ԊǗ��E���ȊO�Ƒ����A���ɂ͕����̂��Ȃ��u�X�^�b�t�Ǘ��E�v������̂ł���B�������}3.8�͉��z��ł��邪�A�����������Ԃ́A���̖̏͂`���ɂ������uE�T�[�r�X���̏����ۑS�T�[�r�X����v�̃f�[�^�����Ă����炩�ł���B�Ȃɂ���A8�l�̐E��ŁA�ے�3�l�A�W��2�l�A���3�l�Ȃ̂ł��邩��A�ǂ��l���Ă����ڂ̕�������1�l���邩���Ȃ����ł���B���́A���ς͏����̂͂���l���邢�ُ͈�l�ɑ傫���e������̂ŁA���������ꍇ�ɂ́A���ς��W�c���\���Ă���ƍl����ɂ͖�肪����B���̗�ł́A1�l�������đS�������ς�������Ă���A���ڂ̕����̐��̕��z��3.1�ő�\������ƁA�R�����ꂽ�悤�ȋC�ɂȂ�B
�}3.8�@�d�S�Ƃ��Ă̕���
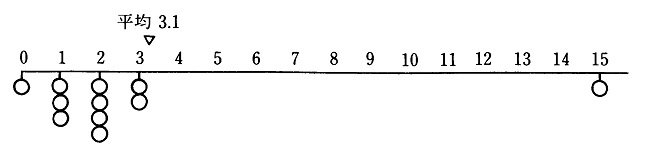
�@���́A��ʂɕ��z���䂪��ł���ꍇ�A�Z�p���ς̂��Ӗ��ɂ��Ă͒��ӂ��K�v�ɂȂ�B���܁A��r�̂��߂Ƀ��f�B�A�����l���悤�B���f�B�A��(median)�͒����l�A���邢�͒��ʐ��Ƃ������A�f�[�^ x1, x2, ..., xn ���������l���珇�ɕ��ׂ����̂� x(1), x(2), ..., x(n) �Ƃ���ƁA���f�B�A���͂��̒����̒l�Ƃ������ƂɂȂ�B�����̃f�[�^�̏ꍇ������̂ŁA���f�B�A���̒�`�͎��̂悤�ɂȂ�B
�@�}3.8�ł̓��f�B�A����2�l�ɂȂ�A����Ȃ�܂�����3.1�l�ł��̕��z���\��������͂܂��̂悤�ł���B��ʂɁA
�@�f�[�^x1, x2, ..., xn�ɑ��āA�E�F�C�gw=(w1, w2, ..., wn) �ɂ����d���ς�
�@�@�@xw��(w1 /��jwj) x1�{(w2 /��jwj) x2�{�������{(wn /��jwj) xn����i=1n(wi /��jwj) xi
�ƒ�`�����B�������Awi��0, i=1, 2, ..., n �ł���Bw1��w2�������wn �̂Ƃ��̉��d���ς͎Z�p���ςƓ������ƂɂȂ�B
�@���̒�`�����ł͈�̉��̖ړI�̂��߂ɉ��d���ς����߂�̂��悭�킩��Ȃ����낤�B���������́A���d���ς͈Öق̂����ɑ��p����Ă���̂ł���B�Ⴆ�A��Ƃ̎��Ȏ��{�䗦�́A���Ȏ��{�䗦�����Ȏ��{�^�����Y �Œ�`����A�e��Ƃ̎��Ȏ��{�Ƒ����Y���킩��A���ꂼ��̊�Ƃ̎��Ȏ��{�䗦���v�Z���邱�Ƃ͊ȒP�ł���B����ł́A�\3.6�̂悤�� n �Ђ̃f�[�^���^����ꂽ�Ƃ��ɂ́A�S�̂̎��Ȏ��{�䗦�͂ǂ̂悤�Ɍv�Z���邾�낤���B�e�Ђ̎��Ȏ��{�䗦���v�Z���āA���̕��ς��Ƃ邾�낤���BSAS���g���A����ȏ����͂��Ƃ����₷���B�������A�\3.6�̂悤�ȕ\���^�����Ă���ƁA���Ȏ��{�̍��v�z���Y�̍��v�z�Ŋ����Ă݂����Ȃ�U�f�ɂ�����B����͖��Ӗ��Ȃ��Ƃ��낤���B���͂��ꂪ���d���ςɂȂ��Ă���̂ł���B
�\3.6�@�����Y�E���Ȏ��{�E���Ȏ��{�䗦
| �@��Ɓ@ | �����Y | ���Ȏ��{ | ���Ȏ��{�䗦 |
|---|---|---|---|
| 1 | x1 | y1 | z1 |
| 2 | x2 | y2 | z2 |
| : | : | : | : |
| n | xn | yn | zn |
| �S�� | xw | yw | ? |
���Ȏ��{�䗦��yw /xw��(y1+y2+���+yn) /(x1+x2+���+xn)
�@�@�@�@�@�@��{x1 /(x1+x2+���+xn)}(y1 /x1)
�{{x2 /(x1+x2+���+xn)}(y2 /x2)
�{�������{{xn /(x1+x2+���+xn)}(yn /xn)
�@�@�@�@�@�@��{x1 /(x1+x2+���+xn)}z1
�{{x2 /(x1+x2+���+xn)}z2
�{�������{{xn /(x1+x2+���+xn)}zn
�܂�A�����Y�z�ɂ����d���ςƂȂ��Ă���̂ł���B�����̏ꍇ�A�e�Ђ̎��Ȏ��{�䗦���v�Z���āA���̕��ς����߂����̂����A���̉��d���ς̕��������I�ɂ́A�͂邩�ɈӖ������邾�낤�B���������āA�R���s���[�^��SAS���g���āA���ł�����ł��͂܂����ɕ��ς����߂�悢�Ƃ������̂ł͂Ȃ��B
�@�x�����z�\���畽�ς��ߎ��I�ɋ��߂�ꍇ�ɂ́A���̉��d���ς��g����B��ʂɁAm �g�̃f�[�^�����݂ɂ����S�f�[�^�̕��ς͊e�g�̕��ς��T�C�Y�ɂ���ĉ��d���ς������̂ƂȂ�B
�\3.7�@�O���[�v�̃T�C�Y�ƕ���
| �O���[�v | �@�T�C�Y�@ | �@���ρ@ |
|---|---|---|
| 1 | n1 | x1 |
| 2 | n2 | x2 |
| : | : | : |
| m | nm | xm |
| �S�� | n | x |
�܂�A���܃O���[�v k �� i �Ԗڂ̃f�[�^�� xki �ŕ\���ƁA
�@�@�@x ��(1/n)(��i=1n1 x1i
�{��i=1n2 x2i�{������
�{��i=1nm xmi)
�@�@�@�@��(n1/n){(1/n1)��i=1n1 x1i}
�{(n2/n){(1/n2)��i=1n2 x2i}�{������
�{(nm/n){(1/nm)��i=1nm xmi}
�@�@�@�@��(n1/n) x1
�{(n2/n) x2�{������
�{(nm/n) xm
�����ŁA�O���[�v1, 2, ..., m�́A�J�e�S���[�ł��������A�K���ł������̂ł���B���������āA���̍l�����́A�ʓI�f�[�^�̓x�����z�\����̑S�f�[�^�̕��ς̎Z�o�ɓK�p���邱�Ƃ��o����B�v�Z�@���g�p���ĕ��ς��v�Z�ł���ꍇ�ɂ͕K�v�̂Ȃ����Ƃł��邪�A����[�̒i�K�ŊK���Ƀv���R�[�f�B���O���Ă���ꍇ�ɂ͎��̂悤�Ȏ葱�����K�v�ɂȂ�B�܂�A
�@�e�K���̋�Ԃł̈�l���z�����肷�邱�Ƃ��ł���A�e�K���ł̕��ρA�K���l�ŋߎ��ł���B���ۂɂ́A�e�K���̋�Ԃł̈�l���z���قډ���ł���̂ŁA���ς��v�Z����Ƃ������Ƃ́A�K���l(class value)���v�Z����Ƃ������ƂɂȂ�B�K���̋��E ai, bi ���킩���Ă���A�K���l mi �͎��̒�`�̂悤�ɂ������ĊȒP�Ɍv�Z�ł���B
�@�@�@mi��(ai�{bi)/2,�@i=1, 2, ..., k
�������A���͊K���̋��E�ł���B�K���̋��E ai, bi �ɂ��Ă͕ϐ��Ƃ��̊ϑ��l�̐������l�����邱�Ƃ��K�v�ɂȂ�B
�}3.9�@�K���u50�_�ȏ�`60�_�����v�̓_���̈�l���z�ƕ���
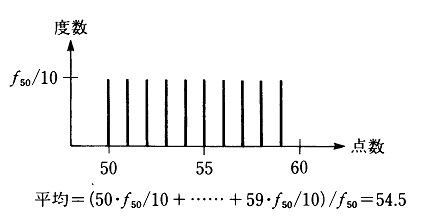
�@�ׂ������Ƃ̂悤�ł��A�K���l��0.5�|�C���g�����Ƃ������Ƃ͖����ł��Ȃ��傫���ł���B�܂�A�s���ӂɕ��ς��v�Z����A�v���R�[�f�B���O���������ƂŁA���ϔN��╽�ϑ̏d�A���ϓ_�����ꂼ��0.5�A0.5kg���邢��0.5�_������Č��_���o���Ă��܂��̂ł���B
�@�T�C�Y n �̂��ׂĐ��̃f�[�^ x1, x2, ..., xn �̊���(geometric mean) G ��
�@�@�@G��(x1�Ex2�E����Exn)1/n
�Œ�`�����B���̊��ς͎��n��I�ɓ���ꂽ�ω��̔䗦�ς���ꍇ�Ȃǂɗp������B
�@�Ⴆ�A�����Ƃ�3�N�Ԃ̔��㍂�̑ΑO�N�L�ї����A20���A25���A20���������Ƃ��A����3�N�Ԃ̔N���ς̔��㍂�L�ї��͎��̂悤�Ɋ��ςŋ��߂���B
�@�@�@G��(1.20�E1.25�E1.20)1/3��1.801/3��1.216
�������A�����3�N�ԂŔ��㍂�� 1.20�E1.25�E1.20��1.80 ��80���L�тĂ���̂ŁA���̂悤�ɍl���邱�Ƃƌ��Ǔ����ł���B�܂�A�����Ƃ̔��㍂��3�N�Ԃ�1.8�{�ɂȂ����B���N�����L�ї�G�Ŕ��㍂���L�тĂ���Ƃ���ƁA3�N�ԂŔ��㍂��1.8�{�ɂȂ�悤��G�����߂��
�@�@�@G�EG�EG��G3��1.8
�@���@G��1.81/3��1.216
���̂悤��G��N���ς̔��㍂�L�ї��ƍl����̂ł���B
�@�������A���̗Ⴉ����킩��悤�ɁA���ςł͌��ʓI�ɓr���̐����̓����͂��ׂČv�Z�ɓ���Ȃ����ƂɂȂ�B���̂��Ƃ�m�炸�Ƀf�[�^���W�߂�ƁA���������W�߂��f�[�^����������Ȃ��P�[�X���N���肤��B�Ⴆ�A�����ŁA�����Ƃ̔��㍂���A����100���~�ŁA����3�N�Ԃ�120���~�A150���~�A180���~�ƐL�т����Ƃ��킩�����Ƃ��悤�B���̂Ƃ��A3�N�Ԃ̑ΑO�N���㍂�L�ї� 120/100(=1.20), 150/120(=1.25), 180/150(=1.20) �̊��ς�
�@�@�@G��(120/100)�E(150/120)�E(180/150)1/3��1.81/3��1.216
�ƂȂ�B�������A���̎����悭����ƁA���ς̌v�Z�̓r���ŁA���q���ꂪ�݂��ɏ��������̂ŁA���ǂ̂Ƃ���A���� G �͍ŏ��ƍŌ�̔��㍂100���~��180���~�������f���Ă��Ȃ����Ƃ��킩��B�܂�A���m�� a, b, c ���܂��̎��ł��\���Ȃ̂ł���B
�@�@�@G��(a/100)�E(b/a)�E(180/b)1/3��1.81/3��1.216
���̂��Ƃ́A�t�ɔ��ɒ����ɂ킽��A�Ⴆ��50�N�Ԃ̕��ς̔��㍂�L�ї��ł����Ă��A���́A���ς��g������́A�ŏ��̔N�ƍŌ�̔N�̔��㍂�f�[�^��������A�r���̃f�[�^���������蔲���Ă��Ă��v�Z�ł���Ƃ������ƂɂȂ�B
�@�Ƃ���ŁA���ӂ̑ΐ����Ƃ�ƁA���ς̑ΐ��́A�ϑ��l��ΐ��ɕϊ������Ƃ��̎Z�p���ςɓ������̂ŁA���v�p�b�P�[�W���g���Ƃ��ɕ֗��ł���B
�@�@�@log G��(log x1�{log x2�{�c�c�{log xn)/n��(��i=1n log xi)/n
�@�x�����z�����E�Ώ̂ŁA���������ĕ��ςƃ��f�B�A�����������Ƃ��ł��A����4�̕��z�̌`�͖��炩�ɈقȂ�A���̂��Ƃ͐}3.10�̂悤�ɖ_�O���t�����Ƃ͂����肷��B
A: 1, 1, 1, 2, 2, 2, 3, 3, 3
B: 1, 1, 2, 2, 2, 2, 2, 3, 3
C: 1, 2, 2, 2, 2, 2, 2, 2, 3
D: 2, 2, 2, 2, 2, 2, 2, 2, 2
�}3.10�@���ς��������āA���U�̈قȂ镪�z
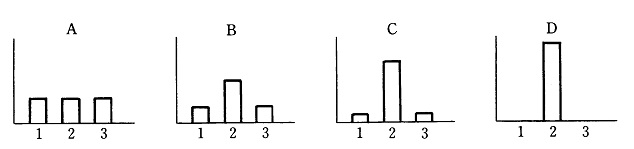
4�̕��z�͂���������E�Ώ̂ŁA���̕��ς�2�ł���B�������A���z�̌`�͖��炩�ɈقȂ��Ă���B����͎��͕��z�̎U����Ă�����x(�t�Ɍ����A���z�̂����܂��Ă�����x)���قȂ��Ă��邩��ł���B���̒��x��\����\�I�Ȃ��̂����U�ł���B
�@�f�[�^x1, x2, ..., xn�̕��U(variance)�͎��̂悤�ɒ�`�����B
�@�@�@sx2��{��i=1n (xi�|x)2}/n
��{(x1�|x)2�{(x2�|x)2�{����{(xn�|x)2}/n
�����ŁA���U�̕��q�͕����a(sum of squares)�܂��͕ϓ��ƌĂ�A
�@�@�@Sx��nsx2��{��i=1n (xi�|x)2}
����xi2�|2x��xi�{nx2
����xi2�|2nx2�{nx2
����xi2�|nx2
�@���U�͂��̂悤�ɕ������a��p���Ă���̂ŁA���̒P�ʂ͊ϑ��l�̒P�ʁA�܂�ϐ��̑���P�ʂ�2��ł���B�����ŁA�ϑ��l�Ɠ���̒P�ʂɂ��邽�߂ɕ��U�̐��̕��������Ƃ����W�������L�����p�����B������ƒ�`���Ă����A�W����(standard deviation)��
�@�@�@sx��(sx2)1/2
�̂悤�ɒ�`�����B
�@�C�ӂ̒萔a, b�ɑ��āAax+b �̕��U��
�@�@�@sax+b2
��{��(axi+b�|(ax+b))2}/n
��{��(axi+b�|(ax+b))2}/n
��{��(a2(xi�|x)2}/n
��a2sx2
�ƂȂ�B�܂�A���̂悤�Ȑ���������B
�@�@�@sax+b2
��a2sx2
�@���z�̎U����Ă�����x��\�����̂Ƃ��ĕ��U��W�������l�������A���͕��U��W�����ł͕��z�̎U������`���I�ɔ�r�ł��Ȃ��悤�ȏꍇ������B���̂悤�ȂƂ��ɂ́A�ϓ��W��(coefficient of variation)
�@�@�@C.V.��(sx/x)�~100
���p������B�ϓ��W���͂��̒�`�̂悤��%�ŕ\�����Ƃ������B��̓I�ɂ́A�ϓ��W���͊ϑ��l�����ׂĐ��̂Ƃ��A���̂悤�ȃP�[�X�ő��ΓI�ȎU������r����̂ɗp������B
�@�ϓ��W���́A���Ƃ��Α���P�ʂ̈قȂ�f�[�^(�������Am��cm�̂悤�Ɍ��_�̈�v���Ă��鑪��P��)���r����ꍇ�ɗp������B���̂Ƃ��A���ςƕW�����͓����P�ʂȂ̂ŁA�ϓ��W���͖������ƂȂ�A��r���\�ɂȂ�B�܂�Ayi��axi, i=1, 2, ..., n, a>0 �Ƃ����Ă�
�@�@�@sy /y�~100��{(asx)/(ax)}�~100��(sx /x)�~100
�ƂȂ�̂ŁA����P�ʂ��قȂ��Ă��Ă��ϓ��W���͕ς��Ȃ��Ƃ����������g���Ă���̂ł���B
�@�Ⴆ�A�n��Ԍ��������i���̃f�[�^�ɂ��ƁA1965�N�̕��Ϗ�����26.6���~�A�W������7.5���~�A1975�N�̕��Ϗ�����117.5���~�A�W������23.8���~�ł������B�W��������������ƁA1965�N�̕������|�I�ɏ������B�������A1975�N��1965�N�ɔ�ׂāA���Ϗ����͖�4.5�{�A�W�����͖�3�{�ƂȂ��Ă���A���ΓI�Ȓn��ԏ����i����1975�N�̕����������Ȃ��Ă���Ƃ����Ă悳�������B���̂悤�ɁA����P�ʂ������ł����Ă����S�̈ʒu���������قȂ�f�[�^�̏ꍇ�ɂ́A�ϓ��W�����p������B1965�N�̕ϓ��W����28.2�A1975�N�̕ϓ��W����20.3�ƂȂ�A�m���ɁA1975�N�̕����ϓ��W���͏������Ȃ�B
�@���I�f�[�^���J�e�S���[A�ƃJ�e�S���[��A���������Ȃ��Ƃ��A2�l���I�f�[�^�ƌĂ��B������1�͑�3���ŏq�ׂ��ړx�ɂ��ϑ��l�̉��Z�\�����J��Ԃ��A
�@�܂��A���ς��l����ꂽ�悤�ɁA2�l���I�f�[�^�̕��U���l���邱�Ƃ��o����B���ς��J�e�S���[A�̔䗦 p �ɂȂ��Ă���̂ŁA���U�͎��̂悤�ɂȂ�B
�@�@�@sx2��{��(xi�|x)2}/n
��[{(1�|p)2�{�����{(1�|p)2}�{{(0�|p)2�{�����{(0�|p)2}]/n
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@f1�@�@�@�@�@�@�@�@�@�@�@f0��
�@�@�@�@��[f1(1�|p)2�{f0(0�|p)2]/n
��p(1�|p)2�{(1�|p)p2��p(1�|p)
���������āA���U�� p��1/2�ōő�l1/4���Ƃ邱�ƂɂȂ�B�Ƃ���ŁA���̂��Ƃ���A�W�����͊e�J�e�S���[�̔䗦�̊��ςɂȂ��Ă���̂ł���B
�@���̂悤��2�l���I�f�[�^�̏ꍇ�ɂ́A���I�f�[�^�ł����Ă����ʉ����邱�Ƃ��\�ƂȂ�A���̂��Ƃɂ��A��荂�x�̉��Z��K�v�Ƃ��铝�v��@���g�p���邱�Ƃ��\�ƂȂ�B�������A���̂悤�ȕ��@�́A���Ĕ�Ȃ���̂Ȃ̂Œ��ӂ�����B���܁A�l�̔��f����D��������ǂ������Ȃǂ̕]�����A���Ƃ���
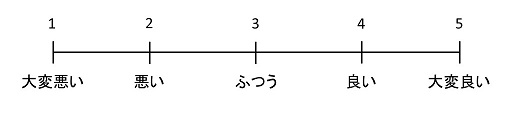
�Ƃ�����5�i�K���炢�œ��������A��1�`5�_�̃X�R�A�ɒu�������邱�Ƃ��l���悤�B���̂悤�ɂ��ē���ꂽ�����̎���̃X�R�A�����Z���ėp����ړx�����b�J�[�g�E�X�P�[��(Likert scale)�Ƃ����B
�@��������5�_�ړx���邢��7�_�ړx�ȂǂŎ���̉����߂邱�Ƃ́A���b�J�[�g�E�X�P�[���Ƃ����ӎ����Ȃ��Ă��A�����ł͂悭�p��������@�ł���B�������A���̕��@�œ���ꂽ�ϑ��l�Ԃ̉��Z���s�����Ƃ́A���͗����̏�ł͖�肪�����B�Ȃ��Ȃ�A�����́A���Ƃ��ΒʐM��̓_�̂悤�ɁA����l��������I�ɕ]���������̂ł͂Ȃ��A�����̐l���܂������Ɨ��Ɏ�ϓI�ɕ]���������̂Ȃ̂ŁA�����ړx�Ƃ��Ĉ������Ƃɂ���^�₪���邩��ł���B�ɂ�������炸�A5�_�ړx�A7�_�ړx�̊ϑ��l�́A�Ƃ肤��l��5�A7�Ƒ������߂ɁA�J�e�S���[�Ƃ��Ĉ����ɂ͕s�ւł���Ƃ������Ƃ������āA���ϒl���Ƃ�����A��蕡�G�ȉ��Z�ɂ��ƂÂ��f�[�^�������s��ꂽ�肷�邱�Ƃ������B�������A���̎�̊ϑ��l���Ԋu�ړx�ȏ�̎ړx�ɂ��ƂÂ��ϑ��l�Ƃ��Ĉ������Ƃɂ́A�O�q�̉��Z�\���̋K�����炢���ƍ������Ȃ��B
�@���������āA5�_�ړx��7�_�ړx�̃f�[�^�������ꍇ�ɂ́A������ȉ��Z�͋�����Ȃ��B�אS�̒��ӂ��K�v�ł���B�����A���̕��ϒl���Ƃ�ꍇ�ɂ́A���Ȃ��Ƃ����z�̕�ŁA�P��^(unimodal)�����Ă��邱�Ƃ��m�F���ׂ��ł���B��ȏ゠��ꍇ�ɂ́A���ɏq�ׂ��悤�ɁA���ϒl�ő�\������Ӗ��͂قƂ�ǂȂ��B�܂��A�����̎���̃X�R�A�����Z���ėp����ꍇ�ɂ́A���ڕ��͂��s���Ȃǂ��āA�e���⍀�ڂ̍��Z�̓K�ۂ��������ׂ��ł���B
�@�������A5�_�ړx��7�_�ړx���g���Ē������邱�Ƃ̈�ԑ傫�Ȗ��_�́A5�i�K�]����7�i�K�]�����W�v���͒i�K�ŁA���Ƃ��u�ǂ��v�u�����v�̓�̃J�e�S���[��2�������邱�Ƃ��A���܂�ɖ�����ɂ��邢�͍�דI�ɂ悭�s����Ƃ������Ƃł���B���̏ꍇ�ɂ́A�����I���ǂ���̃J�e�S���[�ɕ��ނ���̂��ŁA�u�ǂ��v�u�����v�̂ǂ���𑽐��ӌ��Ƃ��邩���ґ������ӓI�Ɍ��߂Ă��܂��댯��������B�ʏ�́A�����I�A���Ȃ킿�ړx�̂قڒ����ɕ��z�̕���̂ŁA�قƂ�ǂ̃P�[�X�Œ����ґ��ɜ��ӓI�Ȕ��f�����߂Ă��邱�ƂɂȂ�B�ŏI�I�Ɂu�ǂ��v�u�����v�̓�̃J�e�S���[�ɂ܂Ƃ߂����Ȃ�A�����i�K�Ŏ���̉̑I�������u�ǂ��v�u�����v�ɂ��Ă����ׂ��ł��낤�B
�@SAS���g���A�ϐ��̕��ρA���U���v�Z���邱�Ƃ͊ȒP�ł���BMEANS�v���V�W�����g���A�킸�����s�ōςށB
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC MEANS [����] DATA=libname.�i�vSAS�ް����Ė��{��; [VAR �ϐ����̕���;] [OPTIONS NOCENTER;]�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC MEANS DATA=SAVE.JPC; �@�@�@VAR TII1--TVI15; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC MEANS [����] DATA=�i�vSAS�ް����Ė�; [VAR �ϐ����̕���;] [OPTIONS NOCENTER;]�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
PROC MEANS DATA=SAVE.JPC; �@�@�@VAR TII1--TVI15; �@�@�@OPTIONS NOCENTER; RUN; |
�@CMS��SAS�̃v���O�����͌`���I�ɂ�PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�BVAR�����ȗ�����ƁA���ׂĂ̐��l�ϐ��ɂ��ċ��߂���BPROC MEANS���̃I�v�V�������ȗ�����ƁA�����l�łȂ��I�u�U�[�ׁ[�V������(N)�A�ő�l(Minimum)�A�ŏ��l(Maximum)�A����(Mean)�A�W����(Std Dev)�ɂ��ċ��߂���B��ȃI�v�V�����Ƃ��Ă͎��̂悤�Ȃ��̂�����B
| �@�@CV | ������ | �ϓ��W�������߂� |
| �@�@MAX | ������ | �ő�l�����߂� |
| �@�@MIN | ������ | �ŏ��l�����߂� |
| �@�@MEAN | ������ | ���ϒl�����߂� |
| �@�@N | ������ | �����l�łȂ��I�u�U�[�ׁ[�V�����������߂� |
| �@�@STD | ������ | �W���������߂� |
| �@�@SUM | ������ | ���v�����߂� |
| �@�@VAR | ������ | ���U�����߂� |
�}3.11�@SAS�ŋ��߂����ρA���U
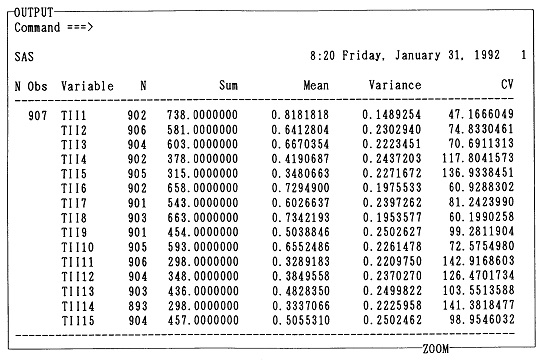
�@�����ŁA�ϐ�TII1�`TVI15�́A���Ƃ��Ƃ́u�g�D�������̂��߂̏]�ƈ��ӎ������v��Yes-No�`���̑S����75��ɑΉ�����ϐ��ł��邪�A��2�͑�6��(5)�̒ʏ�^SAS�v���O�����̒��ŁAYes-No�`���̎���̉ŁA�u1. Yes�v�Ȃ��1�A�u2. No�v�Ȃ��0�Ƃ����l���Ƃ�悤�ɍĒ�`���Ă��������̂ł���B���������āA���̏͂̑O�߂ň�����2�l���I�f�[�^�̕��ςƕ��U�����߂����ƂɂȂ�B�܂�A�e�ϐ��̕��ς�Yes�䗦�������Ă���B�Ƃ���ŁA���U��Yes�䗦��No�䗦(��1�|Yes�䗦)�̐ςɂȂ��Ă���͂��ł��邪�A���ۂɌv�Z���Ă݂�ƁA�����_�ȉ�3���܂ł�����v���Ă��Ȃ����Ƃ��킩��B���̂��Ƃ��炷��ƁASAS�̕��U�̗L��������3�����x�̂悤�ł���B����ȏ�̌����X�Əo�͒ʂ�ɏ����ڂ��Ă����Ӗ��ł���B
�@���K���z(normal distribution)�́A�K�E�X(C.F.Gauss, 1777-1855)���V���ϑ��f�[�^�̑���덷�̌�������덷���_���m�������ۂ̌덷��(error function)�����^�ƂȂ������̂ł���B���̂��߁A���K���z�̂��Ƃ��K�E�X���z(Gaussian distribution)�Ƃ������Ƃ�����B
�@���σʁA���U��2�̐��K���z�� N(��,��2) �ŕ\���B�}3.12�ł͗l�X�Ȑ��K���z�̌`��`���Ă��邪�A���K���z N(��,��2) �͕��σʂ𒆐S�ɂ��č��E�Ώ̂̋ϐ��̂Ƃꂽ�x���^�����Ă���B���σʂōő�l 1/{(2��)1/2��} ���Ƃ�A�ʁ}�Ђ��ϋȓ_�ƂȂ��Ă���B���σʂ̒l���ς��ƁA���z�S�̂����E�ɕ��s�ړ����A���U��2�̒l���傫���Ȃ�ƁA���z���S�̓I�ɕ��ׂ������L����Ƃ�������������B
�}3.12�@���K���z
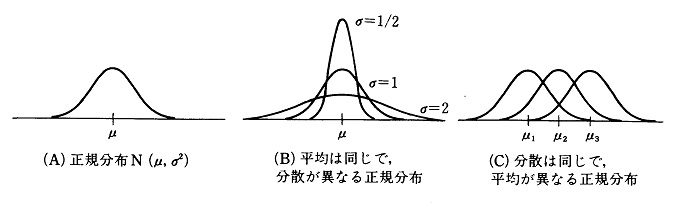
�@�ɂ�������炸�A�m���ϐ� X �����K���z N(��,��2) �ɂ��������A�Ⴆ�Ύ��̂悤�Ȃ��Ƃ��킩���Ă���B
�@�@�@Pr(�ʁ| �Ё�X���ʁ{ ��)��0.683
�@�@�@Pr(�ʁ|2�Ё�X���ʁ{2��)��0.955
�@�@�@Pr(�ʁ|3�Ё�X���ʁ{3��)��0.997
�����}������ƁA�}3.13�̂悤�ɂȂ�B
�}3.13�@���K���z�ƕW����
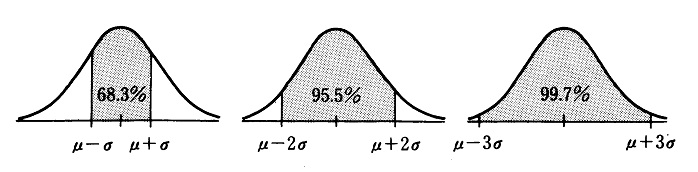
�@���̂��Ƃ͔��ɏd�v�Ȃ��Ƃł���B��W�c�̑��Γx�����z�𐳋K���z�ŋߎ��ł���悤�ȏꍇ�A���̕�W�c���u���K��W�c�v�ƌĂԂ��A���̂悤�ɁA����W�c�̓����l�̕��z�����K���z�ŋߎ��ł���悤�ȏꍇ�ɂ́A���z�̕���x�ƕ��U sx2 ���킩��A�Ⴆ�A��� [x�|sx, x�{sx] �ɂ�68.3%�A��� [x�|2sx, x�{2sx] �ɂ�95.5%�A��� [x�|3sx, x�{3sx] �ɂ͎��ɑS�̂�99.7%�������Ă��邱�Ƃ��킩��̂ł���B���������āA���K���z�͍��E�Ώ̂�����A���R�A��� (-��, x�|sx] �Ƌ�� [x�{sx, ��) �ɂ͂Ƃ��� (100-68.3)/2��15.85% �������Ă���Ƃ����悤�Ȃ��Ƃ��킩���Ă��܂��B����́A�ʂɕW���� sx �̐����{�Ɍ��������Ƃł͂Ȃ��A����l x ������ x ����W���� sx �̉��{����Ă���̂������킩��悢�̂ł���B�Ⴆ�A���[x�|1.96sx, x�{1.96sx]�ɂ͑S�̂�95%�������Ă���(��1�͑�7���̏ꍇ)�B�����ł��ܕϐ� x �����̂悤�ɕϐ� z �ɕϊ����邱�Ƃ��l���Ă݂悤�B�����W����(standardization)�Ƃ����B
�@�@�@z��(x�|x)/sx
���� z �͕W�����_(standard score)�܂��� z ���_(z-score)�ƌĂ��B���̕W�����_�ɂ��ẮA��`���A
�@�@�@z��(x�|x)/sx��0
�@�@�@sz2��sx2/sx2��1
�܂�A�W�����_ z �̕��ς�0�A�W������1�Ƃ�������������B����������A����0�A�W����1 (���������āA���U��1)�̕ϐ��ɕϊ����邱�Ƃ��u�W�����v�Ȃ̂ł���B���������āA�W�����_�͕���0�A���U1�̐��K���z N(0,1) �ɂ����������ƂɂȂ�B���� N(0,1) �͕W�����K���z�ƌĂ��B
�@����W�c�̓����l�����K���z�����Ă���ƍl������ꍇ�ɂ́A�e�l�̕��z�S�̂̒��ł̈ʒu��m�邽�߂ɂ́A���̕W�����_�����͂ȕ��@�ƂȂ�B�܂�A�W�����_�� z ���Ƃ������Ƃ́A�W��������O�̂��Ƃ̒l���A���ς���W������ z �{����Ă���Ƃ������Ƃ������Ă���B���������āA�W�����_�͂��ꂾ���őS�̂̒��ł̈ʒu(�Ⴆ�A��ʁ������A���邢�͏ォ�灛�Ԗڂ��炢)�̏��������炵�Ă����̂ł���B�Ⴆ�A���܂���l�������̕W�����_ z��2 �ł��邱�Ƃ��킩��A�W�����_ z��2 �ȏ�̎҂͑S�̂� (100�|95.5)/2��2.25% �ɂȂ�̂ŁA���������2.25%�ɂ��邱�Ƃ��킩��B���ɑ��Ґ���10,000�l�ł������Ȃ�A�����͏ォ��225�ԑO��ł��邱�Ƃ܂ł킩���Ă��܂��B�l���Ă݂�ƁA�ʏ�͏��ʂ�m�邽�߂ɂ́A�S�̂_���ɕ��ג����Ă݂Ȃ��Ă͂����Ȃ��͂��Ȃ̂ɁA��������Ȃ��Ă��A���ςƕW����(���邢�͕��U)�����킩��A�W�����_���v�Z���Ă�邱�ƂŁA�S�̂̒��ł̂����悻�̈ʒu��m�邱�Ƃ��o����̂ł���B���̈Ӗ��ŁA�W�����_�͋��͂ł���B
�@�������ʂ̒ʒm�Ȃǂɂ悭�p������u���l�v(deviation score)�́A�W�������ꂽ�ϐ� z ���玟�̂悤�Ɍv�Z�����B
�@�@�@���l��50�{10z
�܂�A���l�͕���50�A�W����10�ƂȂ�悤�ɓ_����ϊ��������̂ł���B���������āA�W�����_�Ɠ��l�ɁA�S�̂̒��ł̈ʒu�̏��������炵�Ă���邱�ƂɂȂ�B
�@���ہA�������ʂɌ��炸�A��W�c���z�ɐ��K���z�����肷�邱�Ƃ���ʓI�ɍs���Ă���B�Ⴆ�A�g���⑪��덷�̕��z�ȂǁA���K���z�ŕ\���镪�z�������B���̑��ɂ��A�Ⴆ�A�����͑ΐ����Ƃ�Ɛ��K���z�ŕ\���邱�Ƃ��m���Ă��邪�A���̂悤�ɓK���ȕϐ��ϊ����{���ƁA���K���z�ŕ\������̂������Ƃ������Ƃ��m���Ă���B
�@���܁A��Ƃɑ���W�{�������s���A�W�{�ɂ��āA�j���ʂɕ��ϔN������߂Ă݂�ƁA�j�q�]�ƈ��̕��ϔN���38.2�A���q�]�ƈ��̕��ϔN���28.8�ł������Ƃ��悤�B����10�߂�����������킯�����A���̕��ϔN��������āA����̒�����Ƃł́A�j���̕��ϔN��ɂ͍�������ƌ��_���Ă��悢���̂��낤���B�Ђ���Ƃ���ƁA��W�c�ł͒j���̕��ϔN��ɂ͍����Ȃ��̂ɁA�W�{�덷�̂��߂ɁA����̕W�{�ł͕��ϔN��ɍ����o�Ă��܂����̂�������Ȃ��B�����Ƃ��A�펯�I�ɍl���āA��W�c�ł͍��̂Ȃ��������̂��A�W�{�덷�����ŁA10�������o��Ƃ͍l���ɂ����B���́u10�������o��Ƃ͍l���ɂ����v�Ƃ������x���A�m�����g���ĕ\�����ċᖡ���悤�Ƃ����̂��A���ϒl�̍��̌���ł���B2�Q�̕��ϒl�̍��̌���́A�ʏ́ut ����v(t-test)�Ƃ��Ă悭�m���Ă�����̂ł���B
�@��W�c�̂����Ă��镪�z���W�c���z�ƌĂԂ��A��W�c���烉���_���ɑ傫�� m �̕W�{ (X1, X2, ..., Xm) ��I�ԂƁA�e Xi �͂��̕�W�c���z�ɏ]���m���ϐ��ł���ƍl������B��W�c���z������ ��1�A���U ��12 �̐��K���z N(��1, ��12) �ŋߎ�����鐳�K��W�c�̏ꍇ�A�W�{����
�@�@�@X��(X1�{X2�{����{Xm)/m
�͐��K���z N(��1, ��12/m) �ɂ����������Ƃ��m���Ă���B
�@���܁A������̕�W�c����̕W�{ (Y1, Y2, ..., Yn) �ɂ��Ă��A�W�{���ς�
�@�@�@Y��(Y1�{Y2�{����{Yn)/n
�Ƃ���ƁA��W�c���z�� N(��2, ��22) �̂Ƃ��A���l�ɁAY �͐��K���z N(��2, ��22/n) �ɂ����������ƂɂȂ�B���܉��ɁA�ꕪ�U ��12�A��22 �����m�ł���A�e�Q�̕W�{���ς����ł͂Ȃ��A2�Q�̕W�{���ς̍� X�|Y �����K���z N(��1�|��2, ��12/m�{��22/n) �ɂ����������Ƃ��킩���Ă���B
�@���܉����Ƃ��āu2�Q�̕ꕽ�ς��������v�܂�A
�@�@�@H0: ��1����2
�𗧂Ă�B���̉����̉��ł́A��1�|��2��0 �Ȃ̂ŁAX�|Y �̕W�{���z�� N(0, ��12/m+��22/n) �ɂ����������Ƃ������ɂ킩��B�܂�A�W���������
�@�@�@Z��(X�|Y)/(��12/m�{��22/n)1/2�@�@�@(3.1)
�����K���z N(0,1) �ɂ����������ƂɂȂ�B
�@�������A��ʂɂ́A�ꕪ�U�͖��m�ł킩��Ȃ��B�����ŁA�ꕪ�U�̑���ɁA�s�ΕW�{���U���g�����Ƃ��l���悤�B�����ŁA�s�Ε��U(unbiased variance)�ƌĂ��̂́A���̊��Ғl���ꕪ�U�Ɉ�v���邩��ł���B�ꕪ�U�̑���ɕW�{���U���g�����ƂŁA���z�͐��m�ɂ͐��K���z�ł͂Ȃ��Ȃ��Ă��܂��B���K���z�Ǝ����`������ t ���z���邢�̓X�e���[�f���g(Student)�� t ���z�ƌĂ�镪�z�ɂȂ�̂ł���B���̂��Ƃ́A�S�Z�b�g(William Gosset, 1876-1937)�ɂ���Č��������ꂽ���̂ŁA�X�e���[�f���g�Ƃ͔ނ��_���������ۂɎg�����y���l�[���ł���Bt ���z�́A�W�����K���z N(0,1) �Ɠ��l�ɕ���0�ɂ��č��E�Ώ̂ŁA�W�{�̑傫�����傫���ꍇ�ɂ́A�W�����K���z N(0,1) �ƂقƂ�Ǖς��Ȃ��B���� k���� �̂Ƃ��́A�W�����K���z N(0,1) �ƈ�v����B
�@�����������Ƃ��킩���Ă���̂ŁA�W�{���U���g���ɂ͎��̓�̃P�[�X���l������B
�@���̂Ƃ��A2�Q���������Čv�Z���������������U(pooled variance)
�@�@�@s2���o��(Xi�|X)2�{��(Yj�|Y)2}/(m�{n�|2)�@�@�@(3.2)
���l����ƁA(3.1)���ł� ��12�A��22 �̑���� s2 ���������m���ϐ�
�@�@�@T��(X�|Y)/(s2/m�{s2/n)1/2�@�@�@(3.3)
�����R�x m�{n�|2 �� t ���z t(m�{n�|2) �ɂ����������Ƃ��킩���Ă���B���������āA�W�{���ςƕ��U��(3.3)���ɑ�����ċ��߂��l�� t �Ƃ���ƁA�m���ϐ� T �̐�Βl�����̎��ۂ̊ϑ����ꂽ�l t �̐�Βl�ȏ�ƂȂ�m��
�@�@�@Pr(|T|��|t|)����
���v�Z���ċ��߂邱�Ƃ��ł���(���ۂɂ̓R���s���[�^���v�Z���Ă����)�B�܂�A�u�W�{���ς̍��̐�Βl�����ꂾ���傫���Ȃ�m����100��%�����Ȃ��v�Ƃ������Ƃ��v�Z�ł���̂ł���B��1�͑�6���ł��q�ׂ��悤�ɁA���v�w�ł́A�ʏ킱���L�ӊm����5%�����̂Ƃ��A�u������������������A�W�{���ς̍������ꂾ���傫�Ȓl���Ƃ邱�Ƃ��߂����ɋN���Ȃ��v�Ɣ��f����B���������āA�W�{���狁�߂� t �̒l�Ƃ�����������A��W�c�ɂ��Ẳ��� H0: ��1����2 �͊��p����邱�ƂɂȂ�B�܂�A�����͐������Ȃ��A�ꕽ�ς͓������Ȃ��Ɣ��f����̂ł���B
�@�t�ɁA�������̗L�ӊm����5%�ȏ�̂Ƃ��́A��W�c�ɂ��Ẳ��� H0: ��1����2 ���������Ă��A���̒��x�� t �̒l�͕W�{�덷�Ƃ��ĕW�{���o�゠�肤�邱�Ƃƍl���A�����͍̑������B�܂�A�ꕽ�ς͓������Ɣ��f����̂ł���B
�@���̏ꍇ�́AX�|Y �̐��m�ȕW�{���z�����߂邱�Ƃ͂ł��Ȃ��B�ߎ��I�ɋ��߂���@�Ƃ��āA�E�F���`�̋ߎ��@(Welch's test)���m���Ă���B�e�Q�ł̕W�{���U��
�@�@�@s12��{��(Xi�|X)2}/(m�|1)
�@�@�@s22��{��(Yj�|Y)2}/(n�|1)
�Ƃ���ƁA�m���ϐ�
�@�@�@T��(X�|Y)/(s12/m�{s22/n)1/2
���ߎ��I�ɁA���R�x��
�@�@�@�ˁ�(s12/m�{s22/n)2
/{(s12/m)2/(m�|1)�{(s22/n)2/(n�|1)}
�ɂ����Ƃ��߂�������*�� t ���z t(��*) �ɂ����������Ƃ��m���Ă���B
�@����ł́A2�Q�̕ꕪ�U�����������ǂ����́A������ɔ��f����悢�̂��낤���B����ɂ́A�����Ƃ��āu2�Q�̕ꕪ�U���������v�܂�A
�@�@�@H0: ��12����22
�𗧂Ă�B���܂��̉���: ��12����22 ����������A�ꕪ�U��(variance ratio)
��12/��22��1 �ƂȂ��Ă���͂��ł���B�������A���ۂɊϑ����ꂽ�W�{���U�� f ��1�ɂ͂Ȃ�Ȃ��B���́A�ϑ����ꂽ�W�{���U��̒l��1���炸�ꂽ����W�{�덷�ƍl���Ă��܂��Ă悢���A����Ƃ��A�W�{�덷�ł͍l���ɂ���(�܂�A�m���I�ɂ͋N���肻�����Ȃ���)�Ƃ������Ƃł���B���́A�W�{���U��
�@�@�@F��s12/s22
�����R�x (m�|1, n�|1) �� F ���z F(m�|1, n�|1) �ɂ����������Ƃ��m���Ă���̂ŁA���̕W�{���U����g���āA���̊m�����v�Z���ċ��߂Ă�邱�Ƃ��ł���B���ۂɂ́A
�@�@�@F'��max {s12, s22}
/min {s12, s22}
��1�����̒l���Ƃ�Ȃ��悤�ɒ�`���ꂽ�A�܂�d�ˌ`���� F ���v��(folded F statistics)�ƌĂ����̂��g���āA
�@�@�@Pr(F' > f' )>��
���v�Z���邱�ƂɂȂ�B���̊m�����v�Z�ł���ƁA�W�{���U�䂪1���炸�ꂽ�l f' ���Ƃ�m����100��%�ł��邱�Ƃ��킩��B���v�w�ł́A�ʏ킱���L�ӊm����5%�����̂Ƃ��A������������������A�W�{���U�䂪1���炱�ꂾ�����ꂽ�l���Ƃ邱�Ƃ��߂����ɋN���Ȃ����Ƃ��Ɣ��f����B���������āA�W�{���狁�߂��W�{���U�� f' �̒l�Ƃ�����������A��W�c�ɂ��Ẳ��� H0: ��12����22 �͊��p����邱�ƂɂȂ�B�܂�A�ꕪ�U�͓������Ȃ��Ɣ��f����̂ł���B
�@�t�ɁA�������̗L�ӊm����5%�ȏ�̂Ƃ��́A��W�c�ɂ��Ẳ��� H0: ��12����22 ���������Ă��A���̒��x�̕W�{���U�� f' �̒l�͕W�{�덷�Ƃ��ĕW�{���o�゠�肤�邱�Ƃƍl���A�����͍̑������B�܂�A�ꕪ�U�͓������Ɣ��f����̂ł���B
�@2�Q�̕��ϒl�� t ����(t-test)�Ŕ�r����SAS�v���O�����́A�����ǂ���TTEST�Ƃ����v���V�W���Ƃ��ėp�ӂ���Ă���B���̎g�p�@�͂������ĊȒP�ł���B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC TTEST DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; CLASS ���ޕϐ�; VAR ���ϒl�����߂�ϐ����X�g;�@�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC TTEST DATA=SAVE.JPC; �@�@�@CLASS I1; �@�@�@VAR AGE; RUN; |
| CMS��SAS |
|---|
|
PROC TTEST DATA=�i�vSAS�f�[�^�E�Z�b�g��; CLASS ���ޕϐ�; VAR ���ϒl�����߂�ϐ����X�g;�@�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
PROC TTEST DATA=SAVE.JPC; �@�@�@CLASS I1; �@�@�@VAR AGE; RUN; |
�@CMS��SAS�̃v���O�����́A�`���I�ɂ�PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�B���Ƃ��Ɓu�g�D�������̂��߂̏]�ƈ��ӎ������v�̔N��K�w��\���ϐ�I2�̓v���R�[�f�B���O���Ă���̂ŁA�N��̊K�������ɐݒ肳��Ă���B�v���O������̒��̕ϐ�AGE�́A���̊K���̑���ɁA�K���l��^���č�������̂ł���(�����K���3.3)�B���ޕϐ��͐��l�ϐ��ł������ϐ��ł����܂�Ȃ��B���̃v���O���������s����ƁAPC��SAS�ł́A20�b��Ő}3.14�̂悤�Ȍ��ʂ���ʂɏo�͂����B
�}3.14�@SAS�ɂ�镽�ϒl�̍��̌���(t ����)
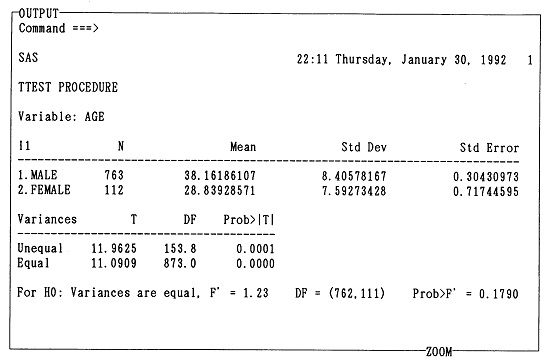
�@���̌��ʂ͎��̂悤�ɓǂނ��ƂɂȂ�B�܂��A�j(1. MALE)�A��(2. FEMALE)�̔N��̕���(Mean)�͂��ꂼ��A38.16����A28.83����ŁA���ꂾ���Ō��Ă��A�ق�10���N�������A�j�̕����A�N������ƌ��������ł��邱�Ƃ��킩��B�W����(Std Dev; 2�悵�����̂����U)���قƂ�Ǔ������̂ŁA���ς��������ꂽ�A�قړ����悤�Ȍ`�̕��z�ɂȂ��Ă���Ƃ�����B
�@���ہA���̕W�{���U��(F')��1.23�ƂقƂ��1�ł���B��萳�m�Ɍ����A���R�x(DF)��763-1=762�A112-1=111�� F ���z�ɂ����������Ƃ��킩���Ă���̂ŁA�W�{���U�䂪����ȏケ�̒l(F')���炸���m��(Prob>F')��0.1790�ŁA�ꕪ�U�͓������Ɣ��f�����B���������āA���U (Variances)��������(Equal)�Ƃ��� t �̒l������悢�B���̒l(T)�́A11.0909�ŁA���R�x(DF)��763+112-2=873�� t ���z�ɂ��������̂ŁA�W�{���ς̍��̐�Βl�� �bt�b��11.0909 �����傫���Ȃ�m��(Prob>|T|)��0.0000�A�܂�1������1�����Ɣ��ɏ������Ȃ�B���̂��Ƃ���W�{���ςɂ͗L�ӂȍ�������A�ꕽ�ς͈قȂ��Ă���ƌ��_�Â�����B
�@�����Ƃ��A�W�{���ς̈Ⴂ�����ꂾ���͂����肵�Ă���A���v�w�̒m�����Ȃ��Ƃ��A�W�{���ς����������ł����f���ł���B�������A�Ⴆ�A���Q�̕��z�̌`���r���邽�߂ɕW�������r����Ƃ����悤�ȃv���Z�X�͏��S�҂Ɍ��炸�A�����Ό����Ƃ��ꂪ���ł���B���v�w�̒m���́A�����������R�K�v�ƂȂ鏈�����܂߂āA�����̓���I�Ȕ��f�A����Β����I�A�펯�I���f�ɑ��āA�q�ϓI�ł�萸�x�̍������f�̍�������Ă���̂ł���B
�@2�Q�̕��ϒl�̔�r�������悤�ɁA���� k �Q�̕��ϒl�̔�r���ł��Ȃ����낤���B���ܕ\3.8�̂悤�� k �Q�̃f�[�^�������A���ꂼ��̌Q�ł̕��ϒl���v�Z�ł����Ƃ��悤�B
�\3.8�@k �Q�̃T�C�Y�ƕ��ϒl
| �@�Q�@ | �T�C�Y | �@���ρ@ |
|---|---|---|
| 1 | n1 | x1 |
| 2 | n2 | x2 |
| : | : | : |
| i | ni | xi |
| : | : | : |
| k | nk | xk |
| �S�� | n | x |
�@���́A2�Q�̕��ϒl�̍��̌����P���� k �Q�Ɋg�����悤�Ƃ��Ă��Ak �Q�̕��ϒl�̍��̌����z�����邱�Ƃ͓���B�����ŁAk �Q�̕��ϒl�̍��̌���̍l�����ɂ��āA�ȒP�ɐ������Ă������B�܂��A�S�����a
�@�@�@S����i=1k ��j=1ni (Xij�|X )2
�͌Q�������a(within samples sum of squares)�̘a�ƌQ�ԕ����a(between samples sum of squares)�ɕ�������Ƃ�������������B�܂�A
�@�@�@S����i ��j [(Xij�|Xi)
�{(Xi�|X )]2
�@�@�@�@����i
{��j (Xij�|Xi)2
�{��j 2(Xij�|Xi)(Xi�|X )
�{��j (Xi�|X )2}
�@�@�@�@����i
{��j (Xij�|Xi)2
�{2(Xi�|X )��j (Xij�|Xi)
�{ni (Xi�|X )2}
�����ŁA��j (Xij�|Xi)��0 �ł��邩��A
�@�@�@S����i
��j (Xij�|Xi)2
�{��ini (Xi�|X )2}�@�@�@(3.4)
�܂�A
�@�@�@�S�����a���Q�������a�̘a�{�Q�ԕ����a
�ƂȂ�킯�ł���B
�@�����ŁA�{��ɖ߂낤�B�uk �Q�̕��ϒl�̍��̌���v�Ƃ͂�萳�m�ɂ́uk �Q�̕W�{�̕ꕽ�ϊԂ̍��̌���v�̂��Ƃł���B�܂�A��W�c�̕��ςɂ��Ẳ���
�@�@�@H0: ��1����2���������k
�����������ǂ��������ƂȂ�B���̉����̂悤�ȊW���W�{�ł��������Ă���A�e�Q�̕��ϒl�͓������A�S�̂̕��ϒl�Ƃ���v���Ă���͂��Ȃ̂ŁA(3.4)���̉E�ӑ�2���̌Q�ԕ����a�̕�����0�ƂȂ��Ă���͂��ł���B�������A���Ƃ��������������Ă��A�W�{���o�̍ۂ̋��R�ɂ���Đ�����W�{�덷�̂��߂ɁA���ꂪ���m��0�ɂȂ�Ƃ����悤�Ȃ��Ƃ͂߂����ɋN���Ȃ��B����ł́A���̕W�{�덷�͂ǂ̒��x�̑傫���ɂȂ�̂��낤���B��������ς���ƁA�Q�ԕ����a���ǂ̂��炢�傫����A�W�{�덷�͈̔͂���E���āA�ꕽ�ϊԂɍ�������ƍl����������Ȃ��Ȃ�̂��낤���B
�@�܂��A(3.4)������A
�@�@�@�Q�������a�̘a���S�����a�|�Q�ԕ����a�@�@�@(3.5)
�ƂȂ�B�����ŁA(3.4)���̉E�ӑ�2���̌Q�ԕ����a�̒�`�������Ă�������悤�ɁA�Q�ԕ����a�́A�e�Q�̕��ϒl�ƑS�̂̕��ϒl�Ƃ̍���2����e�Q�̃T�C�Y�ʼn��d���ĉ��������̂ɂȂ��Ă��邱�Ƃ�������B�܂�A���ϒl�̍��̕����a�ł���B����ɁA�Q�Ԃŕ��ϒl���قȂ邽�߂ɐ��������̌Q�ԕ����a���������c��̌Q�������a�̘a�͋��R�ɂ���Đ������덷�����a(error sum of squares)�ƍl������̂ŁA(3.5)����
�@�@�@�덷�����a���S�����a�|���ϒl�̍��̕����a
�Ə������Ƃ��ł���B���̌덷�����a(���Q�������a�̘a)��P�ʁA��ɂ��āA���ϒl�̍��̕����a(���Q�ԕ����a)���v��A�]�����Ă�邱�Ƃ��l����悢�B
�@�����ŁA�\3.9�̂悤�ȕ\���쐬�����B���̕\�̒��ɂ���u���ϕ����a�v(mean squares)�Ƃ́u�����a�v(sum of squares)�����R�x�Ŋ����ĕ��ς������̂ŁA�s�Ε��U�̂��Ƃł���B���������āA���̕\�ɂ���Čv�Z���ꂽ F��VA/VE �́A���ϒl�̕��U���덷�̕��U�̉��{����̂����݂����̂ɂȂ��Ă���B���́A���� F �����R�x (k�|1, n�|k) �� F ���z�ɂ����������Ƃ��m���Ă���B���̂��Ƃ𗘗p���Č��肪�s���邽�߂ɁA���̌���� F ����Ƃ��Ă��B
�\3.9�@���U���͕\
| �v�� | �����a | ���R�x | ���ϕ����a | F�l |
|---|---|---|---|---|
| �Q�ɂ����� | SA | k�|1 | VA��SA /(k�|1) | F��VA /VE |
| �덷 | SE | n�|k | VE��SE /(n�|k) | |
| �S�� | S | n�|1 |
�@�Ƃ���ŁA���̕\�͕��U���͕\(analysis of variance table)�ƌĂ�邪�A���m�ɂ͂���������A�̎葱���ŁA�ꌳ�z�u(one-way layout)�̕��U���� (analysis of variance)���s��ꂽ���ƂɂȂ�B�������A�����Łu�ꌳ�z�u�v��u���U���́v�̈Ӗ�������ȏ�q�ׂĂ��A���ϒl�̍��̌���Ƃ����ړI�Ƀv���X�ɂȂ�Ȃ��̂ŁA����ȏ�̐����͂��Ȃ����Ƃɂ��悤�B
�@���ɏq�ׂ��悤�ɁAk �Q�̕��ϒl�̍��� F ����́A�l�����Ƃ��ẮA2�Q�̕��ϒl�̍��� t ����̒P���Ȋg���������킯�ł͂Ȃ��B�������A2�Q�̕��ϒl�̍��̌���ɂ��ẮAF ����� t ����������I�ɂ͓������Ƃ����Ă��邱�ƂɂȂ�B���́A2�Q�̕��ϒl�̍��� F ����ŋ��߂� F �l�́A2�Q�̕��ϒl�̍��� t ����ŋ��߂� t �l��2��ɂȂ��Ă���̂ł���B���ہA F��VA/VE �̂����A���� VE �́A
�@�@�@VE��SE /(n�|2)
��{��(X1j�|X1)2�{��(X2j�|X2)2}
/(n1�{n2�|2)��s2
���Ȃ킿�At ����̍ۂ̍����������U(3.2)���Ɠ������Ȃ�B�܂�
�@�@�@X��(n1X1�{n2X2)/(n1�{n2)
�ɒ��ӂ���ƁA���q VA �ɂ��ẮA
�@�@�@VA��SA/1
��n1(X1�|X)2�{n2(X2�|X)2
��(X1�|X2)2/(1/n1�{1/n2)
���������āA F��VA/VE ��(3.3)���� T ��2��ɓ��������ƂɂȂ�B���̂悤�ɁAt ���z�� F ���z�̊Ԃɂ́A�u�� T �����R�x n�|2�� t ���z�ɂ��������Ƃ��́A�� F=T2 �͎��R�x (1, n�|2) �� F ���z�ɂ��������v�Ƃ����W���������̂ł���B�܂�A2�Q�̕��ϒl�̍��� t �����P���Ɋg�����āAk �Q�̕��ϒl�̍��� F ������v�������Ƃ͓���Ă��Ak �Q�̕��ϒl�̍��� F ����̓��ʂ̏ꍇ�Ƃ��āA2�Q�̕��ϒl�̍��� F ������l���A���� F �̒�`���̕��q����̃��[�g���Ƃ邱�ƂŁAt ����� t �̒�`���o���邱�Ƃ͂ł���̂ł���B
�@SAS�ɂ���� k �Q�̕��ϒl���r����ɂ́AGLM�v���V�W�����g�����@���l������B���́AANOVA�v���V�W�����g�����Ƃ��ł��邪�AGLM�v���V�W���̕����A�ėp���������A�g�������o���Ă���Ɠ��ł���B�܂��{���ł͈���Ȃ����A�����v��@�Ɋ�Â��Ȃ��Љ�Ȋw����̃f�[�^�ɑ��ẮA����2���z�u�ȏ�̕��U���͂ɂ�ANOVA�v���V�W���̎g�p�͊��߂��Ȃ��Ƃ����悤�Ȏ��������BGLM�v���V�W�����g���ƁA���̂悤�ɂȂ�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC GLM DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; CLASS ���ޕϐ�; MODEL ���ς��Ƃ�ϐ�=���ޕϐ�;�@�@�@�@�@�@�@�@�@�@�@ MEANS ���ޕϐ�; RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC GLM DATA=SAVE.JPC; �@�@�@CLASS I4; �@�@�@MODEL AGE=I4; �@�@�@MEANS I4; RUN; |
| CMS��SAS |
|---|
|
PROC GLM DATA=�i�vSAS�f�[�^�E�Z�b�g��; CLASS ���ޕϐ�; MODEL ���ς��Ƃ�ϐ�=���ޕϐ�;�@�@�@�@�@�@�@�@�@�@�@ MEANS ���ޕϐ�; RUN; |
| ��) |
|---|
|
PROC GLM DATA=SAVE.JPC; �@�@�@CLASS I4; �@�@�@MODEL AGE=I4; �@�@�@MEANS I4; RUN; |
�@CMS��SAS�̃v���O�����́A�`���I��PC��SAS�̃v���O������1�s�ڂ��폜�������̂ɂȂ�B�����ŁA�v���O������̒��̕ϐ�I4�͐E�ʂ�\���ϐ��ł���B�ϐ�AGE�͑O�߂ō�����N���\���ϐ��ł���B���̃v���O���������s����ƁAPC��SAS�ł͖�40�b�Ő}3.15�̂悤��4��ʂɂ킽���Č��ʂ��o�͂����B
�}3.15�@SAS�ɂ��@k �Q�̕��ϒl�̔�r
�@���̌��ʂ̑�2��ʂ����U���͕\�ɑ������Ă���B��3��ʂ��ގ��̕\�����Ȃ���Ă��邪�A����̔�r�ɂ͊W���Ȃ��̂ŁA��2��ʂ����Ƃɂ��āA���R�x(DF)�A�����a(Sum of Squares)�A���ϕ����a(Mean Square)�AF�l(F Value)�ɒ��ӂ��Ȃ���A���U���͕\�̌`�ɑΉ������ď��������ƁA�\3.10�̂悤�ɂȂ�B�����ŁAF �l�ɂ����u***�v�́A�L�ӊm�� (Pr > F)��0.0001�Ȃ̂ŁA���R0.1%�����ŗL�ӂƂ������Ƃŕ\���������̂ł���B�܂�A���U���͂̌��ʁAk �Q�ɂ�镽�ϒl�̍��͗L�ӂƂ������ƂɂȂ�B�ϐ�AGE�̑S�̂̕���(AGE Mean)�͑�2��ʂ�37.1547756�ƕ\������A�e�Q�ł̕��ς͑�4��ʂɕ\������Ă���̂ŁA�������܂Ƃ߂�ƕ\3.11�̂悤�ɂȂ�B
�\3.10�@���U���͕\
| �v�� | �����a | ���R�x | ���ϕ����a | F �l |
|---|---|---|---|---|
| �Q�ɂ����� | 25501.41639 | 3 | 8500.47213 | 168.66*** |
| �덷 | 43595.01629 | 865 | 50.39886 | |
| �S�� | 69096.43268 | 868 |
�\3.11�@�J�e�S���[����(�e�Q)�̕��ϒl
| �@N�@ | �@���ρ@ | |
|---|---|---|
| 1. �����N���X(GEN) | 72 | 46.3 |
| 2. �ے��N���X(MGR) | 180 | 41.1 |
| 3. �W���N���X(HEAD) | 281 | 40.1 |
| 4. ���(OTHERS) | 336 | 30.6 |
| �S�� | 869 | 37.2 |
�@��2��ʂɕ\������Ă���S�̂̎��R�x868���A��1��ʂ�"NOTE"�ɕ\������Ă���S�̂�N�ɑ�������I�u�U�[�ׁ[�V������869����1���������̂ɂȂ��Ă��邱�Ƃ��m�F���Ăق����B���茋�ʂ��������Ă����悤�ɁA���̕\3.11�ɂ���āA�e�Q�ł̔N��̕��ς̈Ⴂ�����炩�ɂ��邱�Ƃ��킩��B�ے��N���X�ƌW���N���X�̕��ϔN��̍��͍͋��ł��邪�A�����N���X�ƈ�ʂƂł́A����16�����ϔN��Ⴄ�̂ł���B(�����K���3.3)
3.1 �K���̐ݒ�Ɩ_�O���t �@��2��(5)�̗��̉�1�A��2�̖_�O���t��SAS���g���ĕ`���Ă݂�B
3.2 ���U�ƕϓ��W�� �@��6���̐}3.11���Q�l�ɂ��Ȃ���A2�l���I�ϐ��̕ϓ��W�������߂邱�Ƃ̈Ӌ`�ɂ��āA���U�ƑΔ䂵�Ȃ���q�ׂ�B
3.3 ���ϒl�̔�r�Ɩ_�O���t �@�v���R�[�f�B���O���Ă���N��̊e�J�e�S���[�ɑ��āA���̊K���l��^�����ϐ��Ƃ��ĕϐ�AGE��SAS�v���O������Œ�`������ŁA���̂悤�ȓ��v������SAS���g���čs�Ȃ��Ă݂�B
�@����2�ϐ� x, y �̃f�[�^���^�����Ă���ꍇ���l���悤�B�Ⴆ�A��ʓI�ɂ͌l���Ƃ̐g���Ƒ̏d�̃f�[�^�A���邢�͑O�͖`���̗�ł����A�l���Ƃ̐��ʁA�E��A�E�ʂ̃f�[�^�A�����ĕ\4.1�̂悤�Ȋ�Ƃ̎��{���Ə]�ƈ����̃f�[�^�Ȃǂł���B
�\4.1�@���S���16��r(1990�N3��������)
| ��Ж� | ���{��(�S���~) | �]�ƈ���(�l) | ||
|---|---|---|---|---|
| ���@�} | 106,710 | (1) | 7,028 | (6) |
| �߁@�S | 89,851 | (2) | 11,873 | (1) |
| ��@�} | 68,578 | (3) | 5,373 | (7) |
| ���@�S | 65,664 | (4) | 8,268 | (5) |
| ���@�� | 62,971 | (5) | 11,017 | (2) |
| �c�@�c | 58,100 | (6) | 10,572 | (3) |
| ���c�} | 57,606 | (7) | 3,911 | (13) |
| ���@�� | 48,845 | (8) | 4,236 | (12) |
| ���@�� | 40,049 | (9) | 3,371 | (14) |
| ���@�} | 31,396 | (10) | 4,741 | (11) |
| ��@�_ | 27,829 | (11) | 2,230 | (16) |
| ���@�S | 27,143 | (12) | 2,637 | (15) |
| ���@�S | 25,589 | (13) | 8,486 | (4) |
| ��@�C | 22,162 | (14) | 4,855 | (9) |
| ���@�� | 21,665 | (15) | 5,239 | (8) |
| ���@�� | 13,583 | (16) | 4,805 | (10) |
�@�\4.1�͂��Ƃ��Ɓu�g�D�������̂��߂̏]�ƈ��ӎ������v�̑Ώۊ�Ƃ̒��ɁA���S���̂����̉��Ђ����܂܂�Ă������߂ɁA�����̊�Ƃ̋K�͂𑊌݂ɔ�r������A���邢�͋ƊE�̒��ł̈ʒu�Â����s�����肷�邽�߂ɏW�߂�ꂽ�f�[�^�ł���B�ʏ�A��ƋK�͂�\�����邽�߂ɂ悭�p�����鎑�{����]�ƈ������s�b�N�A�b�v���āA���{�����ɕ��ׂĂ݂��B�������A���炩�ɏ]�ƈ������ɂ͂Ȃ��Ă��Ȃ��B���҂�g�ݍ��킹���Ƃ��ɑΏۊ�Ƃ̈ʒu�Â����ǂ����������_�ɂȂ�̂��A���̕\�����ł̓s���Ƃ��Ȃ��B
�@��������2�ϐ��̊Ԃ̊W�̕��͂�1�ϐ��̏ꍇ�Ƃقړ��l�Ɏ��̂悤�Ȏ菇�ōs����B
�@����ł͂܂��A�X�e�b�v1�̐}�E�\�ɂ���ăf�[�^��������@�ɂ��Ă��������邱�Ƃɂ��悤�B���S�҂͂��̃X�e�b�v���y�����āA�����Ȃ葊�ւ��A���������邪�A����ȎG�ōr���ۂ����Ƃ����Ă��ẮA���͂��i��ł��܂�����ŁA������邱�ƂɂȂ�B���̃X�e�b�v1�Ő}�E�\�ɂ���ăf�[�^��������Ɛ������āA�f�[�^�̓����������܂��ɂ���ł����Ȃ��ƁA�X�e�b�v2�łǂ̂悤�ȕ��@��p������悢�̂��A�܂�����ꂽ���l���A�{���Ƀf�[�^��v�����ƂɂȂ��Ă���̂��ɂ��āA��{�I�Ȕ��f���ԈႦ�邱�ƂɂȂ�B
�@���̏͂ł́A�ʓI�f�[�^�̐����E�v����܂��������A���ꂩ����p�ɂɂ���ʓI�ɗp�����鎿�I�f�[�^�̐����E�v��ɂ��Đ������邱�Ƃɂ��悤�B
�@�ʓI�f�[�^�̏ꍇ�ɂ́A���֕\�Ƃ����\�`���A���邢�͎U�z�}(scatter diagram �܂��� scattergram)�Ƃ����}�ɂ���ăf�[�^������B���̂������֕\�ɂ��ẮA������5���Ŏ��グ�邱�Ƃɂ��āA���̏͂ł͎U�z�}�ɂ��Đ������悤�B�U�z�}�Ƃ́A�Ⴆ�ΐ}4.1�͕\4.1�̎��{���Ə]�ƈ�����2�ϐ��̃f�[�^����ɂ��ĕ`�����U�z�}�ł��邪�A���̂悤�ɁA���ʏ�ɒ������W���߂āA�����ɕϐ� x (�}4.1�ł͏]�ƈ���)�A�c���ɕϐ� y (�}4.1�ł͎��{��)���Ƃ�A2�ϐ��f�[�^ (xi, yi), i=1, 2, ..., n �����̍��W���ʏ�ɓ_(1�_���x��1)�ŋL���������̂ł���B
�}4.1�@���S���16�Ђ̎��{���Ə]�ƈ����̎U�z�}
�@�U�z�}����x�����Ŏ菑���ŕ`���Ă݂�Ƃ킩�邱�Ƃ����A���̂悤�Ȃ��������\���̓_���v���b�g���邾���ł��A���͑�ςȍ�Ɨʂł���B�O���t�p���Ɍ������āA�c���A�����̖ڐ����ǂ̒��x�ׂ̍����Őݒ肷�邩��S�Č��߁A���̏�łP�_�P�_���v���b�g���Ă����̂ł���B�������A���̒��x�̌��ł��A�ǂ̓_���ǂ̉�Ђł��������A�`���I�������_�ł͂��͂�킩��Ȃ��Ȃ��Ă���B
�@�U�z�}�́ASAS���g���ΊȒP�ɕ`�����Ƃ��ł���B���̂悤��PLOT�v���V�W����p����悢�B
|
PROC PLOT [DATA=SAS�f�[�^�E�Z�b�g];�@ PLOT �ϐ�1*�ϐ�2[=�ϐ�3]; RUN; |
�@�����ŕϐ�1�A�ϐ�2�͕ϐ��̃��X�g�ł��悢���ƂɂȂ��Ă���B�ϐ�3�͕����ϐ��ł����l�ϐ��ł��悭�A���̕ϐ��̒l�̍ŏ���1�������A�u�_�v�̑���ɕ\������邱�ƂɂȂ�B�ϐ�3�̑���ɁAPLOT X*Y="*"; �̂悤��"*"�Ȃǂ̕����萔��u���ƁA��͂肻�̕����萔�̍ŏ���1�������\�������B�ϐ�3���w�肳��Ȃ���A�x���ɂ���āA�\4.2�̂悤�ɕ\�������B���́APLOT�v���V�W���ɂ���č쐬�����̂́A���m�ɂ͎U�z�}�ł͂Ȃ��A��q����N���X�\����ɂ��ߍׂ����������̂Ȃ̂ł���B���������āA�����ɃZ�����ׂ����ݒ肳��Ă���Ƃ͂����Ă��A��̃Z���ɕ����́u�_�v���u�v���b�g�v���Ȃ��Ă͂Ȃ�Ȃ��悤�Ȏ��Ԃ��U�z�}�ɔ�ׂ�ƕp�ɂɐ����邱�ƂɂȂ�̂ŁA���������x���\�����s����̂ł���B
�\4.2�@SAS�̎U�z�}�ɂ�����x���̕\��
| �x�@�� | �@1�@ | �@2�@ | �@3�@ | �@4�@ | �@5�@ | �@6�@ | �@7�@ | �@8�@ | �@9�@ | �@10�@ | �@11�@ | �@12�@ | ������ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| �\�@�� | A | B | C | D | E | F | G | H | I | J | K | L | ������ |
�ϐ�1�ƕϐ�2�̎w��ɂ��A�U�z�}�̎��͐}4.2�̂悤�ɐݒ肳��邱�ƂɂȂ�B
�}4.2�@�w�肳�ꂽ�ϐ��ƎU�z�}�̎�
�@�Ƃ���ŁA�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̎���[�����ł́A������͎̂��I�f�[�^����Ȃ̂ŁA�U�z�}��`���̂ɓK�����f�[�^���Ȃ��B�����ŁA�����ł́A��قǂ�1990�N3�������݂ł̎��S���16�Ђ̎��{���Ə]�ƈ����̃f�[�^���g����SAS�̃v���O��������l���Ă݂悤�B���̃f�[�^�ɂ��ẮA�܂��i�vSAS�f�[�^�E�Z�b�g�����݂��Ă��Ȃ��̂ŁA�����ł́ASAS�v���O�������ɒ��ڃf�[�^����������ł����āA�������V���ɉi�vSAS�f�[�^�E�Z�b�g�����łɍ���Ă��܂�PC��SAS�̃v���O������������Ă������B
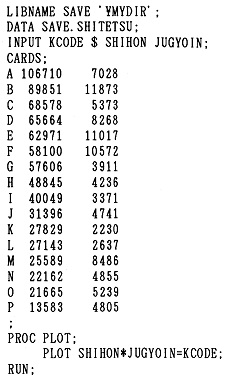
�@���̃v���O������1�s�ڂ��폜����A���̂܂�CMS��SAS�̃v���O������ƂȂ�BPC��SAS�ł́A���̃v���O����������s����ƁA20�b��ʼni�vSAS�f�[�^�E�Z�b�gSHITETSU.SSD���f�B���N�g��MYDIR�̉��ɐ��������ƂƂ��ɁA�}4.3�̂悤�Ȍ��ʂ��o�͂����BCMS��SAS�Ő��������i�vSAS�f�[�^�E�Z�b�g����SHITETSU SAVE�ƂȂ�B
�}4.3�@SAS�ɂ�鎄�S���16�Ђ̎��{���Ə]�ƈ����̎U�z�}
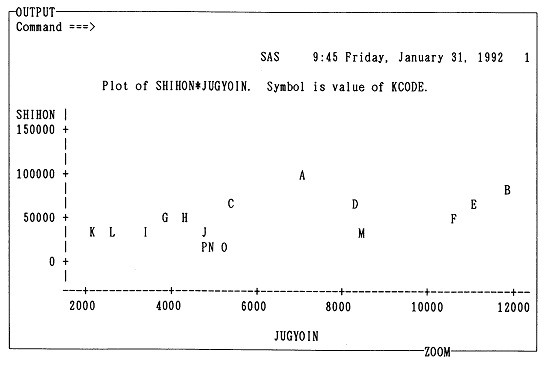
�@��̕ϐ��̊ԂŁA����̒l�����܂�Ƒ����̒l����ӂɒ�܂�W������Ƃ��A���ϐ��̊Ԃɂ͊��W������Ƃ����B����ɑ��āA�����ł������֊W�Ƃ́A��̕ϐ��̊ԂŁA����̒l�����܂�Ƒ����̒l����ӂɒ�܂�Ƃ����킯�ɂ͂����Ȃ��܂ł��A���҂̊ԂɂȂ�炩�̊֘A�����F�߂���W�������Ă���B�Ⴆ�A�ʏ�A�l�Ԃ̐g���Ƒ̏d�̊Ԃɂ́A�g���������قǑ̏d���d���A�̏d���d���قǐg���������Ƃ����W������Ƃ������Ƃ͏펯�I�ɗ����ł���B�������A�g�������܂�Ƒ̏d����ӂɌ��܂�Ƃ����悤�Ȋ��W������킯�ł͂Ȃ��B�����g���ł��A�זڂ̐l���瑾�ڂ̐l�܂ő̏d�ɂ͑傫�ȍ���������̂ł���B
�@���v�w�ŗp�����鑊�֊W�́A���ɒ����I�ȊW���w���Ă�����̂ł���B�܂�A���̂悤�ȊW���w���Ă���B
�@�܂��A���֊W�ƈ��ʊW�Ƃ͕ʂ̊T�O�ł���Ƃ������Ƃɂ����ӂ�����B���֊W�͊ϑ����ꂽ�f�[�^����A�\�ʓI�ɔF�߂��鎖���W�݂̂��Ӗ�����̂ɑ��āA���ʊW�͘_���I�ɍl��������̂ł���B���v�w�ł͎����Ƃ��Ă̑��֊W���������Ƃ͂ł��Ă��A���ꂪ�{���Ɉ��ʊW���Ӗ�������̂��ǂ����v�w�Œ��ڔ��肷�邱�Ƃ͂ł��Ȃ�(��1�͑�2�����Q�Ƃ̂���)�B
�@���ɏq�ׂ��A�U�z�}�⑊�֕\�Ȃǂ̐}�E�\�ɂ���ăf�[�^�����āA���֊W�����o�ɑi���邱�Ƃ��ł���B���̕��@��⊮������̂Ƃ��đ��W��������B���W���́A2�ϐ��Ԃ̑��֊W�̂����A���ɒ����I�ȊW�̋����𑪂�w�W�ł���B���̐߂ł́A���̑��W���ɂ��Ă܂Ƃ߂Ă������B
�@�ʏ�A�P�Ɂu���W���v�Ƃ������ꍇ�ɂ́A�s�A�\���̐ϗ����W��(Pearson's product-moment correlation coefficient ���邢�� Pearson's r)���w�����ƂɂȂ�B2�ϐ��f�[�^ (x1, y1), (x2, y2), ..., (xn, yn) �̃s�A�\���̐ϗ����W���͎��̂悤�ɒ�`�����B
�@�@�@rxy��{��i=1n (xi�|x)(yi�|y)} /[{��i=1n (xi�|x)2}1/2 {��i=1n (yi�|y)2}1/2]
�@���̑��W���͉����Ӗ����Ă���̂��낤�B��`���̕���͕����a�̕������̐ςȂ̂ŁA���̕����͐��Ɍ��܂��Ă���B����ł͒�`���̕��q�͂ǂ����낤���B���W���̒�`���̕��q�ɒ��ڂ��āA���W���̈Ӗ����l���Ă݂悤�B�����ŁA���� (x, y) �����_�Ƃ��钼�����W���l����ƁA�}4.4�̂悤�ɂȂ�B
�}4.4�@���W���̕��q�ƕ���
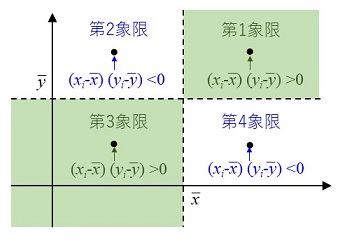
�܂�A���W���̒�`���̕��q�̃��̒��g (xi�|x)(yi�|y) �́A��1�ی����3�ی��ɂ���_�Ōv�Z����Ɛ��A��2�ی����4�ی��ɂ���_�Ōv�Z����ƕ��̒l���Ƃ邱�ƂɂȂ�B���������āA
�@���̂悤�Ȃ��Ƃ���A���W���́A�U�z�}�ȂǑ��֊W�����o�ɑi������@��⊮������̂ł���ƍl���Ă��������ԈႢ���Ȃ��B���W����2�ϐ��Ԃ̒����I�ȊW��v����̂ɂ����Ȃ�����ł���B
�@�Ƃ���ŁA���W���̒�`���̕��q��n�Ŋ���������
�@�@�@sxy��{��i=1n
(xi�|x)(yi�|y)}
/n
�͕ϐ� x �� y �̋����U(covariance)�ƌĂ��B�ϐ� x �� x �̋����U�́A��`���A
�@�@�@sxx��sx2
�܂�A�ϐ� x �̕��U�ƂȂ�B���̋����U��p����A���W����
�@�@�@rxy��sxy /(sxsy)
�ƕ\�����Ƃ��ł���B���̌`�͂��̏͂̒��ł����т��їp������̂ŁA�L���ɂƂǂ߂Ă����Ăق����B
�@���W�� rxy �̒�`�ł́A���� sxsy��0 ���Öق̂����ɉ��肵�Ă��邱�ƂɂȂ�B�������A����͎��ۏ�͂Ȃ�琧��ɂȂ�Ȃ��B�Ȃ��Ȃ�A�Ⴆ�Asx��0, sy��0 �ł���A�ϐ� x �̕W�����A���U��0�Ƃ������ƂɂȂ�Ax �͈��l�̒萔���������ƂɂȂ邩��ł���B���������āA���̃f�[�^�͎����I��2�ϐ��f�[�^�ł͂Ȃ��������ƂɂȂ�A���͂⑊�֊W���l����K�v�͂Ȃ��B
�@���ɁA���W���̂����Ă��鐫������Ă������B�����̐����́A�v�Z�~�X��������ۂ�ASAS�̂悤�ȓ��v�p�b�P�[�W���g���ۂɁA�펯�Ƃ��Ēm���Ă����˂Ȃ�Ȃ�����������W�߂����̂ł���B���ɁA����1�A����2�́A���W�������֊W�̋q�ϓI�w�W�ɂȂ肤�邱�Ƃ��������̂ł��邪�A�m���Ă���Γ��v�p�b�P�[�W�g�p�̍ۂ̐F�X�Ȏ�Ԃ��Ȃ��̂ɖ𗧂B
����1�@���W�� rxy �� x �� y �Ƃ���ꊷ���Ă��ω����Ȃ��B���Ȃ킿 rxy��ryx
����2�@���W�� rxy �̒l�́A���ϐ���1���ϊ� x'��ax+b, y'��cy+d, ac>0 �ɂ���Ă��ς��Ȃ��B���Ȃ킿 rx'y'��rxy
<�ؖ�>
�@�@�@rx'y'
��[��{axi�{b�|(ax�{b)}
{cyi�{d�|(cy�{d)}]
/[[��{axi�{b�|(ax�{b)}2]1/2
[{��cyi�{d�|(cy�{d)}2]1/2]
�@�@�@�@�@��{ac��(xi�|x)(yi�|y)}
/[a{��(xi�|x)2}1/2
c{��(yi�|y)2}1/2]
��rxy�@��
����3�@-1��rxy��1
<�ؖ�>
�@�ŏ��� t �Ɋւ��鎟�̂悤��2�������l����B
�@�@�@h(t)����i [ait�|bi]2
��t2 ��ai2�|2t��aibi�{��bi2
h(t)��0 ������A����2�����̔��ʎ������ɂȂ邱�Ƃ͂Ȃ��A
�@�@�@���ʎ���[��aibi]2�|��ai2 ��bi2��0
����́A�V�����c�̕s����(Schwarz's inequality)�ƌĂ��B������ ai��xi�|x, bi��yi�|y �Ƃ�����
�@�@�@rxy2��{��i=1n
(xi�|x)(yi�|y)}2
/{��i=1n
(xi�|x)2
��i=1n
(yi�|y)2}
��1�@��
����4�@�brxy�b��1 �̕K�v�\�������� (xi, yi), i=1, 2, ..., n �����ׂ� (x, y) ��ʂ铯�꒼����ɂ��邱�Ƃł���B
<�ؖ�>
(�\�����̏ؖ�)
�@ (xi, yi), i=1, 2, ..., n �����ׂē��꒼���� y��ax�{b ��ɂ���Ayi��axi�{b, i=1, 2, ..., n �ƂȂ�A��yi��a��xi�{nb �䂦�ɁAy��ax�{b�B�܂�A(x, y) �����̒��� y��ax�{b ��ɂ���B���������āA
�@�@�@(xi�|x)t�|
(yi�|y)��0, i=1, 2, ..., n�@�@�@(4.1)
������2����
�@�@�@h(t)����[(xi�|x)t�|(yi�|y)]2
��t2��(xi�|x)2
�|2t��(xi�|x)(yi�|y)
�{��(yi�|y)2
���l����ƁA��� h(t)��0 �Ȃ̂ŁAt ��(4.1)����������� h(t)��0 �̏d���łȂ���Ȃ�Ȃ��B����āA
�@�@�@���ʎ�����[(xi�|x)
(yi�|y)]2
�|��(xi�|x)2
��(yi�|y)2
��0
���ꂩ�� rxy2��1
(�K�v���̏ؖ�: �w���@�ŏؖ�����)
�@(4.1)������ t �����݂��Ȃ��Ɖ��肷��ƁA
�@�@�@h(t)����[(xi�|x)t�|(yi�|y)]2��0
�ƂȂ�A���ʎ��͕��łȂ���Ȃ�Ȃ����߂� rxy2��1 �ƂȂ�B����͖����B
����� rxy2��1 �ƂȂ�̂́A(4.1)������ t �����݂���Ƃ��Ɍ�����B���������āA (xi, yi), i=1, 2, ..., n �͂��ׂē��꒼����ɂ���B��
�@��3���ň��������ϒl�̍��̌���̍ۂ� t ����AF ����Ɠ��l�ɁA���W���ɂ��Ă����肷�邱�Ƃ��ł���B��W�c�ł̑��W�����ςƂ����ƁA����
�@�@�@H0: �ρ�0
�����肷�邽�߂ɂ́A
�@�@�@t��rxy(n�|2)1/2/(1�|rxy2)1/2
���A���R�x n�|2 �� t ���z t(n�|2) �ɂ����������Ƃ��킩���Ă���̂ŁA�����p����悢�B
�@�\4.1��(�@)���Ɏ��������{�����ʁA�]�ƈ������ʂ̂悤�ȏ����ړx�f�[�^�ɑ��đ��W����K�p������ǂ��Ȃ邾�낤���B�ړx�̖��(��1�͑�3��(2)���Q�Ƃ̂���)���l����Ɨ��\�Ƃ��������悤���Ȃ����A���܁A�\4.1��(�@)���̏��ʂ��������ē�����悤�ȕ\4.3�̌`��2�ϐ��̏��ʃf�[�^ (x1, y1), (x2, y2), ..., (xn, yn) �ɑ��W����K�p���邱�Ƃ��l���悤�B
�\4.3�@���ʃf�[�^
| �ϑ��Ώ� | �@x�@ | �@y�@ |
|---|---|---|
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| : | : | : |
| i | xi | yi |
| : | : | : |
| n | xn | yn |
�����ŁAxi, yi �͂Ƃ���1���� n �܂ł̐����Ȃ̂ŁA
�@�@�@��xi����yi��1�{2�{����{n��n(n�{1)/2
�@�@�@��xi2����yi2��12�{22�{����{n2��n(n�{1)(2n�{1)/6
�ƂȂ�B���̂��Ƃ�p����ƁAx �� y �̕����a�́A
�@�@�@nsx2��nsy2
����xi2�|nx2
��n(n�{1)(2n�{1)/6�|n(n�{1)2/4��n(n2�|1)/12
�܂�
�@�@�@nsxy����xiyi�|nx�Ey
��[�|��(xi�|yi)2�{��xi2�{��yi2]/2�|nx2
���|��(xi�|yi)2/2�{��xi2�|nx2
���|��(xi�|yi)2/2�{n(n2�|1)/12
���ꂩ��
�@�@�@rxy��sxy /sxsy��1�|6��(xi�|yi)2/{n(n2�|1)}�@�@�@(4.2)
�ƂȂ�B����́A�X�s�A�}���̏��ʑ��W��(Spearman's rank correlation coefficient ���邢�� Spearman's ��)�ƌĂ��B�����ł� rS �Ə������Ƃɂ��悤�B�������A(4.2)���͏��ʃf�[�^��1���� n �܂ł̐����ł��邱�Ƃ𗘗p���Ċȗ��������v�Z���ł����āA���W���̒�`���̂̓s�A�\���̐ϗ����W���Ɠ����ł���B
�@���̌v�Z��(4.2)���̕��q�ɂ��� xi�|yi �ɒ��ڂ���ƁA
�@���ʑ��W���͏��ʂƂ����e������p���Ȃ��B���́A�ʏ�̑��W���͏����̑傫�Ȓl�Ō��܂��Ă��܂��A���ۂɂ͖��Ӗ��Ȑ����ɂȂ邱�Ƃ�����B���̂悤�ȏꍇ�A�������������āA���ʂɕϊ����A���ƂȂ��������āA���ʑ��W�������߂�悢���Ƃ�����B
�@�������ArS �͏��ʂ�\�����l�����������Ԋu�ړx�ł��邩�̂悤�Ɏ�舵���āA�s�A�\���̐ϗ����W�������߂����̂Ȃ̂ŁA��萳�m�ɂ́A���ʂ������ړx�Ƃ��Ĉ������ʑ��W�����g���ׂ��ł���B���̂��Ƃ��l���Ă���̂��A���̃P���h�[���̏��ʑ��W���ł���B
�@�P���h�[���̏��ʑ��W��(Kendall's rank correlation coefficient) �� (�^�E)�́A�����Ɋϑ��l�̑召�W�݂̂f�������W���ł���B���������āA�ǂ��炪�ǂꂭ�炢�傫���Ƃ��������Ƃ�����؍l�����Ȃ��B��قǂƓ��l�ɕ\4.3�̂悤�ȏ��ʃf�[�^���^�����Ă���Ƃ��悤�B���̂悤�ȏ��ʃf�[�^�̑��W���ł���P���h�[���̃т́A���̓�̃P�[�X�ɑΉ����āA��a �ƃ�b ��2��ނ̃т��l���o����Ă���B
�@�̓���̑��l����(�S���� nC2��n(n�|1)/2 �̊ϑ��l�̑�)�A���̊e�����̂悤�ɕ��ނ���B
���ɒ�`��������A�A�t��B�ɉ����āA����2��ނ̓����ʂ��l����K�v������B
�@�����ʂ��Ȃ��ꍇ(��C����D��0)�ɂ́A(4.4)���ɂ��̂��Ƃ�������ƁA(4.3)�Ɠ������ɂȂ�B���Ȃ킿 ��b����a �ƂȂ�B���������āA�����ʂ̂���Ȃ��ɂ�����炸�A��b ���v�Z����悢���ƂɂȂ�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC CORR DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; [VAR �ϐ����̕���;] [WITH �ϐ����̕���;]�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC CORR DATA=SAVE.SHITETSU; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC CORR DATA=�i�vSAS�f�[�^�E�Z�b�g��; [VAR �ϐ����̕���;] [WITH �ϐ����̕���;]�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
PROC CORR DATA=SAVE.SHITETSU; �@�@�@OPTIONS NOCENTER; RUN; |
�@PC��SAS�̃v���O������1�s�ڂ��폜����ƌ`���I�ɂ�CMS��SAS�̃v���O�����ƂȂ�B���̃v���O������ł́A�����قǐ��������i�vSAS�f�[�^�E�Z�b�g(PC��SAS�ł�SHITETSU.SSD�ACMS��SAS�ł�SHITETSU SAVE)���g���āA�S���l�ϐ��Ԃ̑��W�����v�Z�����Ă���B���̃v���O����������s������ƁAPC��SAS�ł�5�b�ȓ��ɐ}4.5�̉�ʂ��o�͂����B��1��ʂł́A�e�ϐ��̃I�u�U�[�ׁ[�V������(N)�A����(Mean)�A�W����(Std Dev)�A���a(Sum)�A�ŏ��l(Minimum)�A�ő�l(Maximum)�Ƃ������P�����v���\������A��2��ʂł́A���W���s�\�������B
�}4.5�@SAS�ɂ�鑊�W���s��̌v�Z
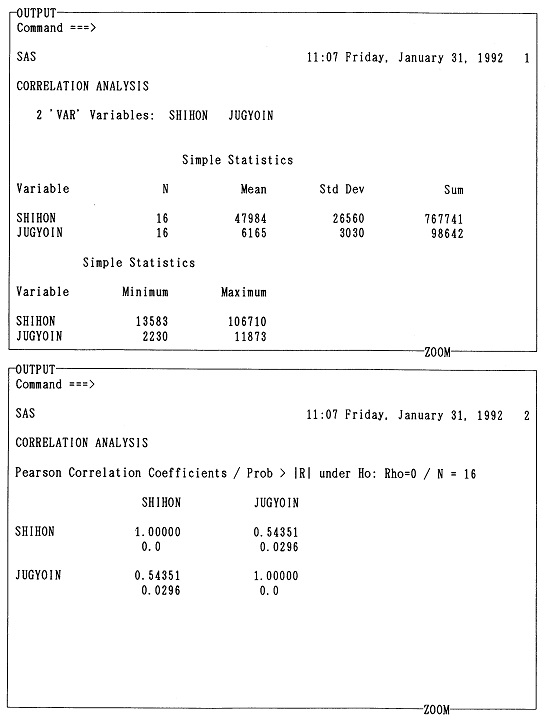
�@��2��ʂŁA���W���s��̊e�Z���̏�i�ɕ\������Ă���̂����W���A���i�ɕ\������Ă���̂��L�ӊm���ł���B���̗�̏ꍇ�ASHIHON��JUGYOIN�Ƃ̊Ԃ̃s�A�\���̐ϗ����W����0.54351�ŁA�L�ӊm����2.96%�Ƃ������ƂɂȂ�B�ʏ�̂悤�ɁA�L�Ӑ�����5%�Ɛݒ肵�Ă���ꍇ�ɂ́A�u5%�����ŗL�Ӂv�Ƃ������ƂɂȂ�B�������A���̏ꍇ�A�����Ŏ�舵���Ă��鎄�S���16�Ђ̃f�[�^�͉����ʂ̕�W�c����̖���וW�{�̃f�[�^�Ƃ����킯�ł͂Ȃ��B�ނ��낱�ꎩ�̂���W�c�Ƃ����Ă悢���낤�B���������āA���v�w�I�ɂ́A���W���͈Ӗ������邪�A��������肷�邱�Ǝ��͖̂��Ӗ��ł���B�����Ƃ��A���̂悤�ȏꍇ�ł��A�L�ӊm����L�Ӑ����L���Ă����̂��A���݂̂Ƃ���u���V�v�ɂȂ��Ă���B�u����͖{���I�ɂ��������I�v�Ɩڂ�����𗧂Ă��ɁA���̏ꍇ�ɂ́A���W��0.54351���u���ւ�����v�Ƃ����Ă��悢�قǂ̐����̒l�Ȃ̂��ǂ����̈�̔��f�ޗ��ɂȂ��Ă���Ƃ������x�ɗ������Ă������������B�q�ϓI�Ȕ��f�ޗ��ɂȂ肤����̂ɑ��Ă��×~�ł��葱����̂����v�����̊�{�I�p���Ȃ̂ł���B�������A���v�w�I�ɂ́A�����܂ł�����וW�{�f�[�^�łȂ�����A�L�ӊm���ɈӖ��͂Ȃ��Ƃ������Ƃ͓��̕Ћ��ɂƂǂ߂Ă����Ăق����B
�@�܂��P�����v�́A�f�[�^�̓������`�F�b�N����Ƃ����_�ł͏d�v�ȏ��ł��邪�A���ɁA��3���ōs�����悤�ȁA1�ϐ��f�[�^�Ƃ��Ă̋ᖡ���I�����Ă���ꍇ�ɂ́A���߂ă`�F�b�N����K�v�͂Ȃ��B���̂Ƃ��́APROC���ŒP�����v�͂���Ȃ��Ƃ������ƂŁANOSIMPLE�Ǝ��̂悤�ɉ�������lj��w�肵�Ă��ƁA�P�����v�͏o�͂��ꂸ�A���W���s�����o�͂����B
�@�@�@PROC CORR NOSIMPLE DATA=SAS�f�[�^�E�Z�b�g��;
�������͂��߂̍��́A���̓s�x�A�P�����v���܂߂Ƀ`�F�b�N����K�������Ă�������������ł���B
���W���s��́A�ϐ��̐��������Ă���ƁA�L�Ӑ�����
| + | �@p<0.1 | �@(10%) |
| * | �@p<0.05 | �@(5%) |
| ** | �@p<0.01 | �@(1%) |
| *** | �@p<0.001 | �@(0.1%) |
�̂悤��+���*��ŕ\�������������₷���B�������A�L�Ӑ������ǂ̂悤�ɐݒ肷��̂��͕��͂��鑤�̈Ӑ}�Ɉˋ����Ă���̂ł��邪�A�����ɋ������悤�ȗL�Ӑ����̋��A10%�A5%�A1%�A0.1%�́A�M�҂��܂߂đ����̐l�ɗp�����Ă�����̂ł���B���ʂȎ�`�A�咣�̂Ȃ�����A�������̗p������������ł��낤�B�܂��A�ʏ�́A5%�����ł͂��߂ėL�ӂƌ����邱�Ƃ������A10%�����ł́u�L�Ӂv�Ƃ͈����Ȃ��̂ŁA�u�Q�l���x�Ɂv�Ƃ����Ӗ������߂āA*����g�킸��+��ŕ\������B
�@���������āA���|�[�g��_���ő��W���s��������ꍇ�ɂ́A�\4.4�̂悤�ɕ\������悢�B���W���͑Ίp����͂��ׂĂP�ɂȂ邵�A�܂��Ίp���ɑ��đΏ̂ɂȂ��Ă���̂ŁA�E�㔼���������͍������������������ςނ��ƂɂȂ�B�����̓s���ł��̂悤�ɏȗ����邱�Ƃ����邪�A���₷���Ƃ������Ƃ������A�����̋�������A�ȗ������ɕ\�����Ă��悢���낤�B
�\4.4�@���W���s��
| �@���{���@ | �@�]�ƈ����@ | |
|---|---|---|
| ���{�� | �@1.000*** | �@0.544* |
| �]�ƈ��� | �@0.544* | �@1.000*** |
�@�Ƃ���ŁASAS�v���O�����́u�ϐ����̕��сv�̒��̕ϐ��͐��l�ϐ��Ɍ�����B�܂��v���O������ł͏ȗ����Ă��܂������A�������VAR����WITH�����ȗ������Ɏg�p���A���W�����v�Z����ϐ����m�Ɏw�肷��̂���{�ł���BWITH����VAR�����ȗ������ꍇ�ɁA���ꂼ��ǂ��������������Ȃ����̂��������Ă������B
�@���̏ꍇ�ɂ́A�ȗ����ꂽWITH���ɂ�VAR���Ɠ����ϐ����̕��т��w�肳��Ă���Ɖ��߂����B�܂�A���̓�̃v���O�����͓����@�\���ʂ����B
|
(A) PROC CORR DATA=SAVE.SHITETSU; �@�@�@VAR SHIHON JUGYOIN; RUN; |
|
(B) PROC CORR DATA=SAVE.SHITETSU; �@�@�@VAR SHIHON JUGYOIN; �@�@�@WITH SHIHON JUGYOIN; RUN; |
�@���̏ꍇ�ɂ́A�w�肳�ꂽSAS�f�[�^�E�Z�b�g�̑S�Ă̐��l�ϐ��������̑ΏۂƂȂ�B�܂�A���̓�̃v���O�����͓����@�\���ʂ������ƂɂȂ�B
|
(C) PROC CORR DATA=SAVE.SHITETSU; RUN; |
|
(D) PROC CORR DATA=SAVE.SHITETSU; �@�@�@VAR _NUMERIC_; RUN; |
�@���ǁA���̃v���O������Ŏg�p���Ă���i�vSAS�f�[�^�E�Z�b�g�ł́A���l�ϐ���SHIHON��JUGYOIN�̓�����Ȃ��̂ŁA4�̃v���O������(A)(B)(C)(D)�͓����������s�����ƂɂȂ�B
�@�X�s�A�}���̏��ʑ��W���A�P���h�[���̏��ʑ��W�������߂����ꍇ�ɂ́A�s�A�\���̐ϗ����W�������߂�v���O������CORR�̃I�v�V�������������ꂼ��
�@�@�@PROC CORR SPEARMAN DATA=SAS�f�[�^�E�Z�b�g��;
���邢�́A
�@�@�@PROC CORR KENDALL DATA=SAS�f�[�^�E�Z�b�g��;
�Ɖ����������������邾���œ��l�ɂ��ċ��߂���B
�@�\4.1�̃f�[�^���g���ƁA���{���Ə]�ƈ����Ƃ̊Ԃ̑��W���͕\4.5�̂悤�ɂȂ�B���̕\������킩��悤�ɁASPEARMAN��KENDALL���w�肵�����ɂ́A���ʃf�[�^�ł͂Ȃ��A���z�E�l���f�[�^��^�����ꍇ�ł��A���̏��ʂɂ��Ă̑��W�������߂���B���������āA���z�E�l���f�[�^�ł����ʃf�[�^�ł����W�� rS�A��b �͕ς��Ȃ��B�܂��A���ʃf�[�^��^���ċ��߂��s�A�\���̐ϗ����W�� r ���A��`�ʂ�X�s�A�}���̏��ʑ��W�� rS �ƈ�v���邱�Ƃ��m�F�ł���B
�\4.5�@�\4.1�̃f�[�^�ɂ���SAS�ŋ��߂��e�푊�W���ƗL�ӊm��
| ���z�E�l���f�[�^ | ���ʃf�[�^ | |||
|---|---|---|---|---|
| ���W�� | �L�ӊm�� | ���W�� | �L�ӊm�� | |
| �s�A�\���̐ϗ����W�� r | 0.54351 | 0.0296 | 0.46471 | 0.0697 |
| �X�s�A�}���̏��ʑ��W�� rS�@ | 0.46471 | 0.0697 | 0.46471 | 0.0697 |
| �P���h�[���̏��ʑ��W�� ��b | 0.30000 | 0.1051 | 0.30000 | 0.1051 |
�@����(correlation)���Ax �� y ��Γ��Ɍ��āA���݂̊W�������Ă����̂ɑ��āA��A(regression)���͂ł́A�Ⴆ�� x ���� y �����肳��������̊W������(�������t�����ɁAy ���� x �����肳���Ƃ����W���������Ƃ��ł���)�B2�ϐ��f�[�^�ɒ���(1����)�����Ă͂߂�ɂ́A���̓�̖����l����K�v������B
���1�@y��a�{bx ���T�C�Y n ��2�ϐ��f�[�^ (x1, y1), ..., (xn, yn) �ɂ��܂����Ă͂܂�悤�� a, b �����߂�B
�@�����ŁAy��a�{bx �Ƃ������͕ϐ� x �ɂ���ĕϐ� y ��������悤�Ƃ�����̂Ȃ̂ŁA�ϐ� x �͐����ϐ��܂��͓Ɨ��ϐ�(independent variable)�ƌĂ�A�ϐ� y �͔�����ϐ��܂��͏]���ϐ�(dependent variable)�ƌĂ��B���̖����������@�ɂ́A�ŏ�2��@�ƌĂ����@������B�ŏ�2��@�ɂ���ē����钼�����uy �� x �ւ̉�A����(regression line)�v�܂��́uy �� x �ւ̉�A��(regression equation)�v�ƌĂԁB���̂悤�ɁA�ŏ�2��@�ɂ���Ē��������߂邱�Ƃ���A���͂ƌĂсA���̖��1�̂悤�ɐ����ϐ�����̏ꍇ�ɂ́A�P��A�ƌĂԁB�܂��A����ʓI�ɐ����ϐ��� p �̏ꍇ�ɂ́A�d��A(multiple regression analysis)�ƌĂԁB�P��A�͏d��A�̓���ȃP�[�X(p��1)�ł��邪�A�ʏ�́A�d��A�Ƃ����A���ɁAp��2�̏ꍇ���w�����Ƃ������B
���2�@���1�ŋ��߂�ꂽ����(1����)�̃f�[�^�ւ̂��Ă͂܂��𑪂�B
�@����́A���m�ɂ͏d���W���⌈��W�������߂���ɂȂ邪�A�P��A�ł́A���W���̐�Βl�͏d���֊W���ƈ�v���A���W���̂Q��͌���W���Ƃ���v����̂ŁA���W���ɂ���Ă��Ă͂܂��𑪂邱�Ƃ��ł���B
�@����ł́A���1: y��a�{bx ��2�ϐ��f�[�^ (x1, y1), ..., (xn, yn) �ɂ��܂����Ă͂܂�悤�� a, b �����߂邱�Ƃ��l���Ă݂悤�B�ŏ�2��@(method of least squares)�Ƃ́A
�@�@�@��i=1n[yi�|(a�{bxi)]2�@�@�@(4.5)
�@
���ŏ��ɂ���悤�� a, b �����߂���@�ł���B���̒���[�@]���͎c�� ei �ƌĂ����̂ŁA(4.5)���͎c��2��a�Ƃ������ƂɂȂ�B�ŏ�2��@�͂��̎c���Q��a���ŏ��ɂ���悤�� a, b �����߂���@�Ȃ̂ł���B���̂��Ƃ�}������ƁA�}4.6�̂悤�ɂȂ�B
�}4.6�@�ϑ��l�ւ̒����̂��Ă͂�
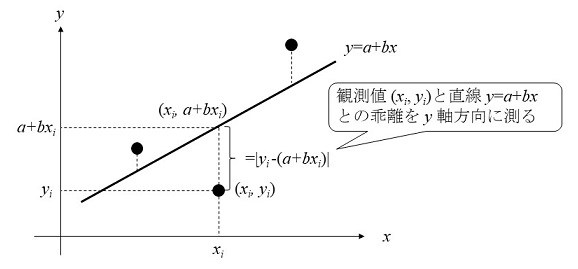
�@�܂�A�c���̐�Βl |yi�|(a+bxi)| �Ŋϑ��l (xi, yi) �ƒ��� y��a�{bx �Ƃ̘����� y �������ɑ���A���� y �������̘�����2��a�ɂ���āA���̒�����2�ϐ��f�[�^ (x1, y1), ..., (xn, yn) �ւ̂��Ă͂܂����v���Ă�낤�Ƃ����̂ł���B
�@�c��2��a���ŏ��ɂ���悤�� a, b �����߂Ă݂�ƁA�܂�ŏ�2��@�ɂ��ƁAa, b �͎��̂悤�ȊȒP�Ȏ��ŋ��߂���B
�@�@�@b����i=1n (xi�|x)(yi�|y)/��i=1n (xi�|x)2��sxy /sx2��rxysy /sx�@�@�@(4.6)
�@�@�@a��y�|bx
���̂悤�ɂ��ċ��߂�ꂽ b ����A�W��(regression coefficient)�Aa ����A�萔���邢�� y �ؕ�(y-intercept)�ƌĂԁB��A�W�� b �̎����疾�炩�Ȃ悤�ɁA�ϐ� x ��y �̕��U���ς��Ȃ���A��A�W�� b �͗��ϐ��̑��W���̑傫���ɔ�Ⴗ�邱�ƂɂȂ�B���W����0�̂Ƃ��͉�A�W�� b ��0�ɂȂ��āA��A������ x ���ɕ��s�ɂȂ�B
<�ؖ�>
�@�@�@Q(a, b)����[yi�|(a�{bxi)]2
�Ƃ����A�����̌���
�@�@�@[{f(x)}n]'��n{f(x)}n-1f '(x)
���g���āAQ(a, b) �� a, b �Ɋւ���Γ��������߁A0�Ƃ����ƁA
�@�@�@��Q(a, b)/��a����2(yi�|a�|bxi)(-1)��0
�@�@�@��Q(a, b)/��b����2(yi�|a�|bxi)(-xi)��0
���������Ɛ��K������(normal equation)�ƌĂ�鎟�̘A����������������B
�@�@�@an�{b��xi����yi
�@�@�@a��xi�{b��xi2����xiyi
���̘A���������������ɂ́A��1���̗��ӂ�n�Ŋ����ē����� a��y�|bx ���2���ɑ�����邱�Ƃɂ���āA
�@�@�@b��(��xiyi�|nx y)/(��xi2�|nx2)��{��(xi�|x)(yi�|y)}/��(xi�|x)2�@��
�@���l�ɂ��āAx �� y �ւ̉�A���� x��a'�{b'y �̉�A�W���A��A�萔�����̂悤�ɋ��߂���B
�@�@�@b'��sxy /sy2��rxysx /sy
�@�@�@a'��x�|b'y
���̂悤�ɂ��āA2�ϐ��f�[�^ (x1, y1), ..., (xn, yn) �ɂ��ẮA�ǂ��������ϐ��ɂ��A�ǂ���������ϐ��ɂ��邩�ŁA2�{�̉�A�������������Ƃ��ł���B����2�{�̉�A�����ɂ��ẮA���̊W�����藧�B
����1�@2�{�̉�A�����͓_ (x, y) �Ō����B
<�ؖ�>
�@y �� x �ւ̉�A���� y��a�{bx �� a��y�|bx ��������� y�|y��b(x�|x) �Ə����邱�Ƃ���A���̉�A������ (x, y) ��ʂ�B���l�ɁAx �� y �ւ̉�A������ x�|x��b'(y�|y) �Ə���
�邱�Ƃ���A���̉�A������ (x, y) ��ʂ�B��
����2�@�ϐ� x �ƕϐ� y �̑��W�� rxy �̐�Βl�� b ��b' �̐�Βl�̊��ςƂȂ�B���Ȃ킿�Ab'b��rxy2
<�ؖ�>
�@�@�@b'b��(rxysx /sy)(rxysy /sx)��rxy2�@��
���̐���2���玟�̐����������ɓ������B
����3�@rxy���}1 �̂Ƃ� 1/b'��b ��2�{�̉�A�����͏d�Ȃ�B
����͐���2�ɂ��Ȃ��Ă����炩�ł��낤�B�Ȃ��Ȃ�Arxy���}1 �̂Ƃ��A���ׂĂ̓_�͓��꒼����ɂ���(���W���̐���4)�킯������A���R�A���̒�������A�����Əd�Ȃ�Ȃ��������������ł���B
�@����ɁAb �� b' �̎�����
����4�@���W�� rxy �Ɖ�A�W�� b, b' �̕����͈�v����B
<�ؖ�>
�@�@�@b��rxysy /sx, b'��rxysx /sy ���疾�炩�B��
�@�Ⴆ�A�����ւ� rxy��0 �ƂȂ��Ă���Ƃ��́Ab��b'��0 ��2�{�̉�A�����͂��ꂼ�� x ���Ay ���ɕ��s�Ȓ����ƂȂ�A�������邱�ƂɂȂ�B
����5�@b'��0 �̂Ƃ� |1/b'|��|b|
<�ؖ�>
�@�@�@0��b'b��rxy2��1
�ł���B���������āAb��0 �̂Ƃ� b'��0 �ł��邱�Ƃ��� 1/b'��b��0�Bb��0 �̂Ƃ� b'��0 �ł��邱�Ƃ��� 1/b'��b��0�B��
�@�ȏ�̐������܂Ƃ߂�ƁA���ւ̑傫����2�{�̉�A�����̊W�͐}4.7�̂悤�ɐ}�������B�}4.7������킩��悤�ɁAy �� x �ւ̉�A���� y��a�{bx �̕�����ɌX�������₩�Ȃ��̂ɂȂ�(����5)�B�������A���ւ��ア�قǁA2�{�̉�A�����̌X���̊J���͑傫�Ȃ��̂ɂȂ�B��A�����̌X���͉�A�W�� b�Ō��܂�̂ŁA��A�W�� b �̐�Βl���������āA��A���� y��a�{bx �̌X�����������Ƃ��ɂ́A���ۂɂ͂��̂悤�ɑ��ւ��キ�A�����P�ɉ�A�����̂��Ă͂܂�̒��x���Ⴍ�A��A�����̐����͂��ア�����Ƃ����\���̂��邱�Ƃɒ��ӂ���K�v������B���́A��A�����̂��Ă͂܂�̒��x�A�����͂�����ɂ́A���W���̑傫��������悢�̂ł���B
�}4.7�@2�{�̉�A�����Ƒ���
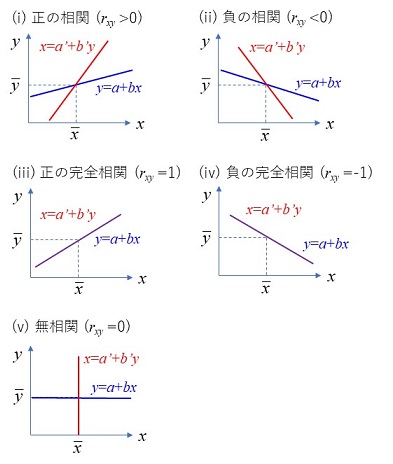
�@��A�����̐����͂����邽�߂ɂ́A������ϐ��̑S�����a ��(yi�|y)2 �̂����A��A���� y��a�{bx �Ő����̂������a�����̊������ǂ̒��x�ɂȂ��Ă���̂��ׂ�悢�킯�����A����ɂ́A��A�����ɂ���Đ����ł��Ȃ������c��2��a�̑S�����a�ɐ�߂銄�����l���A�����1������������̂ɒ��ڂ��Ă��悢�B���������W��(coefficient of determination)�ƌĂсAR2 �ŕ\���B���Ȃ킿�A
�@�@�@R2��1�|[��{yi�|(a�{bxi)}2]/��(yi�|y)2
�P��A�̏ꍇ�ɂ́A�����ϐ��Ɣ�����ϐ��̑��W����2�悪���̌���W���ɓ������Ȃ邱�Ƃ��킩���Ă���B���Ȃ킿�A
�@�@�@rxy2��R2
�@�܂���A�����ɂ��\���l a�{bxi �Ǝ��ۂ̊ϑ��l yi �Ƃ̊Ԃ̑��W�� R �͏d���W��(multiple correlation coefficient)�ƌĂ�A��A�����̂��Ă͂܂�̒��x��\���Ă���ƍl������B�d���W���� 0��R��1 �ł���A�܂��d���W����2��͌���W���Ɉ�v���邱�Ƃ��킩���Ă���B���Ȃ킿�A
�@�@�@(R)2��R2
�@���̂��Ƃ���A�P��A�̏ꍇ�ɂ́A���W���̐�Βl�Əd���W�������������ƂɂȂ�B���������āA���W�����傫���قǁA��A�����̂��Ă͂܂���x���ǂ��A�����͂������Ƃ������ƂɂȂ�̂ł���B
�@����W���͑��W����2��ɂȂ��Ă���̂ŁA���Ƃ��A���W���� r��0.7 �̂Ƃ��A����W���� R2��0.49 �ƂȂ�B�܂�A������ϐ��̑S�����a��0.49�܂�قڔ�����49%����A�����ɂ���Đ�������Ă��邱�ƂɂȂ�A���W���̐����ɔ�ׂĐ����͂��ӊO�ƒႢ���Ƃ��킩��B���W���� r��0.9 �ɂ��Ȃ�A����W���� R2��0.81 �ɂȂ邪�A�t�ɑ��W���������� r��0.3 �ł���A����W���� R2��0.09�A�܂������ϐ��̑S�����a�̂킸��10%�サ�������ł��Ă��Ȃ����ƂɂȂ�B
�@���̂悤�ɁA��A�����̐����͂���������W�����A���W����2��ƂȂ��Ă��邱�Ƃ�����킩��悤�ɁA��A���͂͑��֕��͂Ɛ[���W������A���W�����g���Ƃ��Ɠ��l�̒��ӂ��K�v�ƂȂ��Ă���B���Ȃ킿�A
�@����וW�{�̃f�[�^ (X1, Y1), ..., (Xn, Yn) �ɂ��ƂÂ��ĉ�A���͂��s�����Ƃ��A���߂�ꂽ��A�萔 a�A��A�W�� b �͊m���ϐ��ƂȂ�B��W�c�ł̉�A������ y�����{��x �ŁA���̂Ƃ��̎c���� x �̒l�ɂ��Ȃ������U�̐��K���z�ŋߎ������ꍇ(x �� y �̓������z��2�������K���z�ŋߎ������ꍇ�ɂ����Ȃ邱�Ƃ��킩���Ă���)�A��A�W���ɂ��Ẳ���
�@�@�@H0: ������0
�����肷�邽�߂ɂ́A
�@�@�@t��(b�|��0)/s.e.(b)�@�@�@(4.7)
�����R�x n�|2 �� t ���z�ɂ��������̂ŁA���̂��Ƃ�p����B���l�ɁA��A�萔�ɂ��Ẳ���
�@�@�@H0: ������0
�����肷�邽�߂ɂ�
�@�@�@t��(a�|��0)/s.e.(a)
�����R�xn-2�� t ���z�ɂ��������̂ŁA���̂��Ƃ�p����悢�B�����ŁAs.e.(b)�As.e.(a) �͕W���덷(standard error)�ƌĂ�A���̂悤�ɂȂ�B
�@�@�@s.e.(b)��s/{��(Xi�|X)2}1/2
�@�@�@s.e.(a)��s/{1/n�{X2/��(Xi�|X)2}1/2
�������A
�@�@�@s2����[Yi�|(a�{bXi)]2/(n�|2)��(1�|r2)��(Yi�|Y)2/(n�|2)
�@�����ŁA�����̒��� ��0�A��0 �͕��͂��s���l�����߂�萔�ł��邪�A���ɉ�A�W�� ��0 �ɂ��Ĉ�ʂɂ悭�p������̂� ��0��0 �ł���B�܂�A�u�����ϐ� x �� y �ɉe����^���Ȃ��v�Ƃ��������ł���B���̉����̂Ƃ��� t �̒l�� t �l�Ƃ����B���ł�(4.6)���ʼn�A�W�� b ��
�@�@�@b��rxysy/sx
�ƂȂ邱�Ƃ��q�ׂ����A���̎�������z�������悤�ɁA���̎���s.e.(b)��(4.7)���ɑ������ƁA�P��A�̉�A�W���ɂ��Ẳ��� H0: ����0 �̌���Ƒ��W���ɂ��Ẳ��� H0: �ρ�0 �̌���͓����Ƃ������Ƃ��킩��B
�@��A���͂���v�Z�ōs�����Ƃ́A�f�[�^���������Ă���ƁA��ʂɑ�ςȍ�Ƃł���B�����ŁA���悢��SAS�̂悤�ȓ��v�p�b�P�[�W���L�p�ƂȂ��Ă���B��A���͂��s��SAS�v���O�������������ĊȒP�ł���BREG�v���V�W�����g���悢�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC REG DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; MODEL ������ϐ�=�����ϐ�;�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC REG DATA=SAVE.SHITETSU; MODEL SHIHON=JUGYOIN; RUN; |
| CMS��SAS |
|---|
|
PROC REG DATA=�i�vSAS�f�[�^�E�Z�b�g��; MODEL ������ϐ�=�����ϐ�;�@�@�@�@�@�@�@�@�@�@�@�@�@ RUN; |
| ��) |
|---|
|
PROC REG DATA=SAVE.SHITETSU; MODEL SHIHON=JUGYOIN; RUN; |
�@PC��SAS�̃v���O������1�s�ڂ��폜����ƌ`���I�ɂ�CMS��SAS�̃v���O�����ƂȂ�B���̃v���O����������s����ƁAPC��SAS�ł�10�b�قǂŁA�}4.8�̂悤�ɁA2��ʂ��\�������B��1��ʂ͕��U����(ANALYSIS OF VARIANCE)�\��\�����A��2��ʂ͉�A�W���E��A�萔�̐���l(PARAMETER ESTIMATES)�y�т��̌��茋�ʂ��o�͂����B����ɕK�v�ł���APROC���̃I�v�V�����Ƃ���SIMPLE��lj��w�肷��A���W���̂Ƃ��Ɠ��l�̒P�����v���o�͂����邱�Ƃ��ł���B
�}4.8�@SAS�ɂ���A����(SHIHON��JUGYOIN�ւ̉�A����)
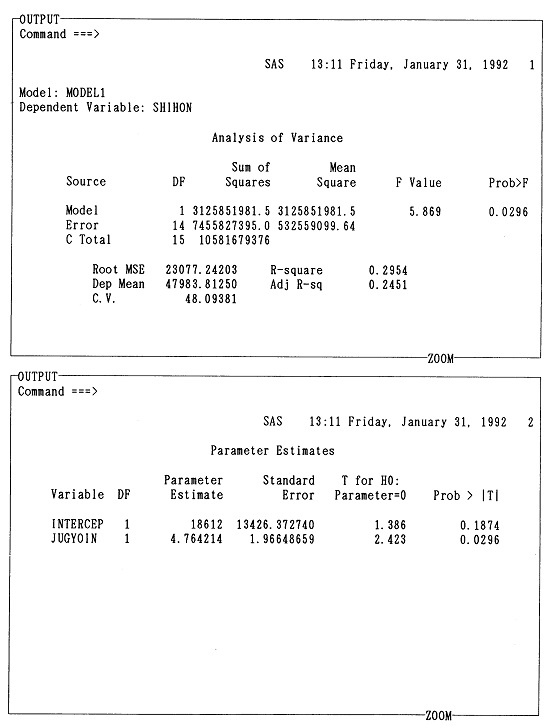
�@���U���͂ɂ��ẮA�����ł͐������Ȃ����A����W�� R2 (R-square)��0.2954�Ɗ�����3���}4.5�ŋ��߂Ă������W��0.54351��2��ɓ��������ƁA�܂���A���͂̃��f���̗L�ӊm��(Prob>F) 0.0296���A���W���̗L�ӊm���Ɠ������Ȃ��Ă��邱�Ƃ��m�F���Ăق����B���̗L�ӊm���́A�����ϐ�JUGYOIN�̉�A�W���̗L�ӊm��(Prob > |T|)�Ƃ��������B���ɏq�ׂ��悤�ɁA�P��A�̉�A�W���ɂ��Ẳ��� H0: ����0 �̌���Ƒ��W���ɂ��Ẳ��� H0: �ρ�0 �̌���͓����Ȃ̂ł���B
�@��A�W���A��A�萔(INTERCEP)�̐���A�����āAt �l(T)����A���̂悤�ȉ�A���͂̌��ʂ�����ꂽ���ƂɂȂ�B
�@�@�@SHIHON��18612�{4.7642 JUGYOIN
�@�@�@�@�@�@�@ (1.386)�@(2.423*)
�����ŁA(�@)���� t �l�������Ă���Bt �l�ɕt����ꂽ*��́A5%�����ŗL�ӂł��邱�Ƃ������Ă���B�܂��A���ƂɂȂ����\4.1�̎��{���f�[�^�̗L�������Ȃǂ��l����ƁA��A�W���A��A�萔�́ASAS�̏o�͌��ʂ�S���������ɁA5�����\������������낤�B
�@���Ȃ݂ɁA�v���O�������MODEL���ŁA�����ϐ��Ɣ�����ϐ������ւ���
�@�@�@MODEL JUGYOIN=SHIHON;
�Ƃ��Ď��s������ƁA�}4.9�̂悤�Ȍ��ʂ��o�͂����B
�}4.9�@SAS�ɂ���A����(JUGYOIN��SHIHON�ւ̉�A����)
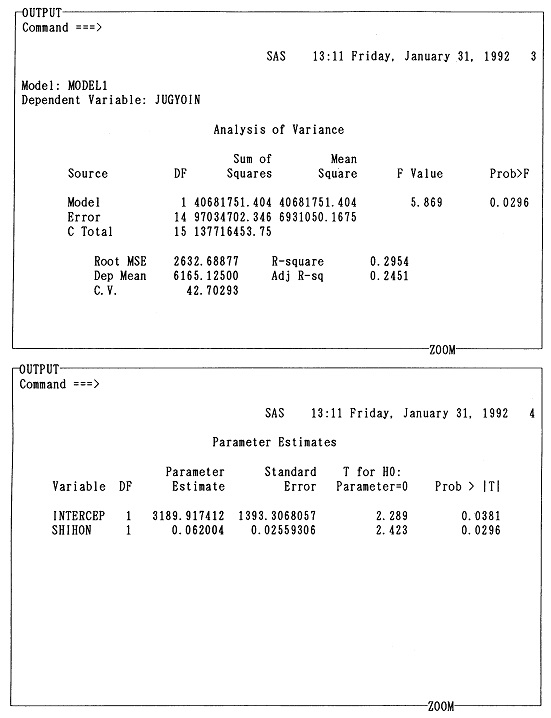
�@�����ϐ��Ɣ�����ϐ������ւ��Ă��A���U���͂� F �l(F Value)�A�L�ӊm��(Prob>F)�A����W��(R-square)�͐�قǂ̒l�ƑS�������ɂȂ邱�Ƃ��m���߂Ăق����B�܂������ϐ�������ւ�����ɂ��ւ�炸�A�����ϐ��� t �l(T)�A�L�ӊm��(Prob > |T|)���ς�炸�A�����ł��邱�Ƃ��m�F���Ăق����B�����Ƃ��A���R�A��A�����͎��̂悤�ɕʂ̂��̂ɂȂ��Ă���B
�@�@�@JUGYOIN��3189.9�{0.062004 SHIHON
�@�@�@�@�@�@�@�@(2.289*)�@(2.423*)
��قNj��߂���A�W��4.7642�Ƃ����ŋ��߂���A�W��0.062004�̊��ς́A
�@�@�@(4.7642�~0.062004)1/2��0.54351
�Ƒ��W���ɓ������Ȃ邱�Ƃ��m�F���Ăق����B
�@���̏͂̍ŏ��ɕ`���Ă������}4.1�̎U�z�}�ɁA2�{�̉�A��������������ł݂�ƁA�}4.10�̂悤�ɂȂ�B
�}4.10�@2�{�̉�A����
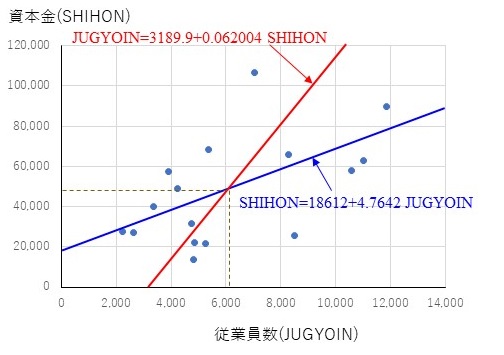
4.1 ���ցE��A����
�@�\4.1�̎��S���16�Ђ̃f�[�^���A���{��(SHIHON)�A�]�ƈ���(JUGYOIN)���̂܂܂ł͂Ȃ��A���̑ΐ����Ƃ�����ŁA���ցA��A���͂��s�Ȃ��Ă݂�BSAS�̃v���O�����ł́A�ϐ�X�̑ΐ��́A�ꂪe�̎��R�ΐ��A�ꂪ10�̏�p�ΐ��A�ꂪ2�̑ΐ��ɂ��ẮA���ꂼ��
�@�@�@Y=LOG(X);
�@�@�@Y=LOG10(X);
�@�@�@Y=LOG2(X);
�Ƃ������悤��(�@)���̊��ŋ��߂邱�Ƃ��ł���B����PC��SAS�̃v���O��������Q�l�ɂ���Ƃ悢�B����1�s�ڂ��폜�����CMS��SAS�̃v���O������ɂȂ�B
LIBNAME SAVE '��MYDIR';
DATA SAVE.SHITETSU;
�@SET SAVE.SHITETSU;
SLOG=LOG(SHIHON);
JLOG=LOG(JUGYOIN);
PROC PLOT;
�@�@�@PLOT SLOG*JLOG=KCODE;
RUN;
PROC REG;
MODEL SLOG=JLOG;
RUN;
4.2 ���ցE��A���� �@�\4.6�̃f�[�^�́A��6����D�d�C����1991�N3�������݂�100%�q��БS14�Ђ̎��{���A�]�ƈ����ł���B���ցE��A���͂��s���Ă݂�B
�\4.6�@D�d�C����100%�q��Ђ̎��{���A�]�ƈ���(1991�N3��������)
| ��� | ���{��(�S���~) | �]�ƈ���(�l) |
|---|---|---|
| A | 2,000 | 779 |
| B | 2,200 | 218 |
| C | 300 | 1,108 |
| D | 300 | 1,214 |
| E | 40 | 579 |
| F | 80 | 404 |
| G | 50 | 830 |
| H | 50 | 1,199 |
| I | 450 | 32 |
| J | 50 | 590 |
| K | 200 | 1,284 |
| L | 50 | 156 |
| M | 200 | 84 |
| N | 450 | 16 |
4.3 ���ցE��A���� �@�����{���q�S��(��) (������uJR�����{�v)�́A1990�N3���������A���{��200,000�S���~�A�]�ƈ�����80,000�l�Ƃ���ꂽ�B�\4.1�̎��S���16�Ђ�JR�����{�������đ��ցE��A���͂��s���Ă݂�B
�@2�ϐ��f�[�^�̕\�́A��ʂɂ́A���I�f�[�^�̏ꍇ�ɂ̓N���X�\(cross table)���邢�͊֘A�\�E�����\(contingency table)�A�ʓI�f�[�^�̏ꍇ�ɂ͑��֕\(correlation table)�ƌĂ��B���I�f�[�^�̕\�ƗʓI�f�[�^�̕\�̗��҂̂��āA��d���ޕ\(double classification table)�ƌĂԂ��Ƃ�����B������ɂ���A�����̕\�́A2�ϐ����ɂƂ肠���������x�����z�̕\�ł���B
�@���ۂɕ\���쐬����Ƃ��ɂ́A�܂���̕ϐ��̒l�����I�f�[�^�ł̓J�e�S���[�A�ʓI�f�[�^�ł͊K���ɕ������āA����ɗ��҂�����(�N���X)���鏡��(�Z��)�ɓx�����������ނ̂ł���B���̈�ʓI�Ȍ`���͕\5.1�̂悤�ɂȂ�B
�\5.1�@2�ϐ��f�[�^�̕\�̈�ʌ`��
| �@x�@ | y | |||||
|---|---|---|---|---|---|---|
| �@y1�@ | ������ | �@yj�@ | ������ | �@yk�@ | �@�v�@ | |
| x1 | f11 | ������ | f1j | ������ | f1k | f1� |
| : | : | : | : | : | ||
| xi | fi1 | ������ | fij | ������ | fik | fi� |
| : | : | : | : | : | ||
| xl | fl1 | ������ | flj | ������ | flk | fl� |
| �v | f�1 | ������ | f�j | ������ | f�k | n |
�@���̌`���ō쐬���ꂽ�\���A���I�f�[�^�~���I�f�[�^�̏ꍇ�̓N���X�\�ƌĂсA�ʓI�f�[�^�~�ʓI�f�[�^�̏ꍇ�ɂ͑��֕\�ƌĂԂ̂ł���B���������āA���I�f�[�^�̃N���X�\�̂Ƃ��́Axi, yi �̓J�e�S���[��\�����ƂɂȂ邵�A�ʓI�f�[�^�̑��֕\�̂Ƃ��ɂ́Axi, yi �͊K����\�����ƂɂȂ�̂ł���B��ʓI�ɂ́A�\���̕ϐ�(�����ł�x)�ɁA����{�I�Ȃ��̂������Ă��邱�Ƃ������B
�@�����ŁA�\5.1�̒��̊e�Z���� fij �������x��������킵�Ă���B�����A�u�v�v�Ƃ��ĕ\�̉����Ȃ킿���ӂɕ\������Ă�����̂́A���ӓx���ƌĂ��B�܂�A
�@�@�@fi�����j fij�@������x�̎��ӓx��
�@�@�@f�j����i fij�@������y�̎��ӓx��
�Ƃ������ƂɂȂ�B
�@�ʓI�f�[�^�ɂ��āA�O�͂ň������U�z�}�́A��ʓI�ɂ͔��ɗL�͂ȕ��@�ł���̂����A�Љ�Ȋw����A���ɒ����f�[�^�̏ꍇ�ɂ́A���܂�[���l���������ɁA�P���ɎU�z�}��`���Ă��A�����̎��p���A���ʂƂ����_�ł͂��܂���҂ł��Ȃ��B�Ȃ��Ȃ�A�{���ň����Ă���u�g�D�������̂��߂̏]�ƈ��ӎ������v�̂悤�ȃP�[�X�ł́A�ϐ������U�ϐ��ł��邱�Ƃ�������(�����Ƃ��A������3�͑�1���ŏq�ׂ��悤�ɁA�ϑ��E����f�[�^�͌����ɂ͂��ׂė��U�I�ł���)�A�������A�Ƃ肤��l�̐��ɔ�ׂăf�[�^�̃T�C�Y���傫���̂�(�܂�A�����ΏێҐ��������̂�)�A�U�z�}��`���Ă݂Ă��A���ʓI�ɎU�z�}�ł͓����ʒu�ɂ������̓_���d�Ȃ荇�����ƂɂȂ�A���ǁA�_�ł͕��z���킩�炸�A�x���Ŏ�����������Ȃ��Ȃ��Ă��܂��B���ɑO�͂ň�����PLOT�v���V�W�����g����SAS�ɕ`������ƁA��ʂ̑傫���̐���������āA�`�������U�z�}���A�����I�ɂ͑��֕\�Ɠ������ƂɂȂ炴��Ȃ��悤�ȏꍇ�������̂ł���B���������āA�u�Ƃ肠�����v�U�z�}��`�����Ă݂邱�Ƃ̌��p��ے肵�͂��Ȃ����A�����ɂ͑��֕\��������ƍ쐬���ׂ��ł��낤�B
�@��3���ň������悤�ɁA�ʓI�f�[�^�Ƃ͂����Ă��A�e�ϐ��͓K�ɊK�����ݒ肳���ׂ��ł���A���ɂ��ꂪ���ɍs�Ȃ��Ă���Ȃ�A���ՂɎU�z�}��`���Ă݂�(SAS���g���Ύ�Ԃ͂�����Ȃ���)�����A���֕\���쐬���������͂邩�Ɏ��p�I�ŁA���ꂢ�ɐ������ł���B���́A��3���ň������悤��1�ϐ��ł̃f�[�^�̋ᖡ�́A����������̕��G�ȏ������ԈႢ������������āA����Ȃ�Ɛi�߂邽�߂ɁA�ɂ߂ďd�v�ł���B2�ϐ��̑��֕\���쐬����i�ɂȂ��āA���̂悤�Ȃ��ƂɔY�ނƂ�����A����́A���������K���ݒ�̑O�H������������ƍs���Ă��Ȃ����Ƃ̏؋��Ȃ̂ł���B
�@���̏͂ł́A2�ϐ��f�[�^�̕\�̊�{�ł��鎿�I�f�[�^�̃N���X�\�ɂ��Đ������悤�B�ʓI�f�[�^�̑��֕\��A���I�f�[�^�ƗʓI�f�[�^��g�ݍ��킹���\���A���̃N���X�\�̉��p�ƂȂ�B
�@2�ϐ��̎��I�f�[�^�̃N���X�\�ŁA��Ԋ�{�I�ł��d�v�Ȃ��̂��A�e�ϐ����e�X��̃J�e�S���[�������Ă���ꍇ�̃N���X�\�ŁA2�~2�N���X�\�ƌĂ��B�l���\(four-fold table)�ƌĂ�邱�Ƃ�����B��Ƃ��āu�g�D�������̂��߂̏]�ƈ��ӎ������v�Œ��ׂ�������g���āA�N���X�\������Ă݂悤�B���ܒj���̐��ʂƓ��Yes-No�`���̎���
�@�@�@V.2. �I�g���̉�ЂŎd�������Ă��������Ǝv���B�@1. Yes�@2. No
�@�@�@V.12. �l���ɂ�Ƃ肪����A�y�����B�@1. Yes�@2. No
�Ƃ̊Ԃł��ꂼ��N���X�\������Ă݂�ƁA�\5.2��(A)(B)��������B����͕M�҂��悭�g���`���̃N���X�\�ł���B
�\5.2�@�N���X�\�̗�
(A)
| ����V2. �I�g���̉�ЂŎd�������Ă��������Ǝv���B | |||
|---|---|---|---|
| �@�@�@1. Yes�@�@�@ | �@�@�@2. No�@�@�@ | �@�@�@�@�v�@�@�@�@ | |
| 1. �j | 508�@(66.67) | 254�@(33.33) | 762�@(100) |
| 2. �� | 38�@(35.19) | 70�@(64.81) | 108�@(100) |
| �v�@ | 546�@�@�@�@ | 324�@�@�@�@ | 870�@�@�@ |
(B)
| ����V12. �l���ɂ�Ƃ肪����A�y�����B | |||
|---|---|---|---|
| �@�@�@1. Yes�@�@�@ | �@�@�@2. No�@�@�@ | �@�@�@�@�v�@�@�@�@ | |
| 1. �j | 282�@(37.01) | 480�@(62.99) | 762�@(100) |
| 2. �� | 68�@(62.39) | 41�@(37.61) | 109�@(100) |
| �v�@ | 350�@�@�@�@ | 521�@�@�@�@ | 871�@�@�@ |
�@�\5.2�̃N���X�\�̒���(�@)���ɂ͍s�����̕S�����������Ă���B�N���X�\�̉��ɂ��Ă��� Cramer's V �Ƃ���2�ɂ��ẮA���ꂩ�炱�̏͂̒��Ő������Ă������ƂɂȂ邪�A����������ւ̒��x��\���Ă�����̂ł���B***�͂��̗L�ӊm����0.1%�������������Ƃ������Ă���BCramer's V�Ƃ���2�ɂ��Ă܂��m��Ȃ��Ă��A�\5.2(A)����͒j�q�]�ƈ��̕����A�I�g���̉�ЂŎd�������Ă��������Ǝv���X�������邱�Ƃ킩�邵�A�\5.2(B)����͏��q�]�ƈ��̕����A�l���ɂ�Ƃ肪����A�y�����Ǝv���Ă���Ƃ��������[���X�����ǂ�Ŏ��邾�낤�B�i�����K���5.1�j
�\5.3�@���߂̂͂����肵�Ă���N���X�\
(A)�����ւ̏ꍇ�@�@�@(B)���̊��S���ւ̏ꍇ
| x | y | ||
|---|---|---|---|
| 1. Yes | 2. No | �v | |
| 1. Yes | 25 | 25 | 50 |
| 2. No | 25 | 25 | 50 |
| �v | 50 | 50 | 100 |
| x | y | ||
|---|---|---|---|
| 1. Yes | 2. No | �v | |
| 1. Yes | 50 | 0 | 50 |
| 2. No | 0 | 50 | 50 |
| �v | 50 | 50 | 100 |
�@��ʓI�ɂ́A������N���X�\�͍ŏI�I�ɂ�2�~2�N���X�\�ɋA��������Ƃ�����قǂŁA2�~2�N���X�\��������Ɨ������A������Ɖ��߂ł��邱�Ƃ��A�N���X�\���p�̊�{�ƂȂ�B�����Ƃ�2�~2�N���X�\��������Ɨ������A������Ɖ��߂��邱�Ƃ͌����ē���Ȃ��B�����\5.3(A)�̂悤�ȃN���X�\������ꂽ��A�ϐ� x �� y �Ƃ̊Ԃɉ��̊֘A���Ȃ��Ƃ������Ƃ́A�͂����肵�Ă���B�����\5.3(B)�̂悤�ȃN���X�\������ꂽ��Ax ��Yes�Ȃ�� y ��Yes�Ax ��No�Ȃ�� y ��No�Ɠ�����Ƃ������S�Ȋ֘A�����邱�Ƃ���ڗđR�ł���B����ł́A���̗��͂ǂ��Ȃ邾�낤���B
���)�@�\5.4�̃N���X�\�ł͎��ӓx���������^�����Ă���B�����Ax �� y �Ƃ̊Ԃɑ��ւ��S���Ȃ������ւł�������A�x���͂ǂ��Ȃ��Ă���͂����낤���B�\5.4(A)�̃N���X�\�ɓx�������������B�܂� x �� y �Ƃ̊Ԃɐ��̊��S���ւ����������\5.4(B)�̃N���X�\�ɓx�������������B
�\5.4�@���̉p�N���X�\
(A)�����ւ̏ꍇ�@�@�@(B)���̊��S���ւ̏ꍇ
| x | y | ||
|---|---|---|---|
| 1. Yes | 2. No | �v | |
| 1. Yes | �@ | �@ | 60 |
| 2. No | �@ | �@ | 40 |
| �v | 60 | 40 | 100 |
| x | y | ||
|---|---|---|---|
| 1. Yes | 2. No | �v | |
| 1. Yes | �@ | �@ | 60 |
| 2. No | �@ | �@ | 40 |
| �v | 60 | 40 | 100 |
�@�����ł́A���̗��̂悤�Ɏ��ӓx������̓I�ɗ^�����Ă����ł͂Ȃ��A��ʂ̏ꍇ�ɂ��ĉ�����悤�B���̉́A�ȉ��̉����ǂ߂����ɂ킩��͂��ł���B���ꂼ�ꎩ���ōl����ꂽ���B
�@�N���X�\�ŁAx �� y �Ƃ̊Ԃɑ��ւ��S���Ȃ��ꍇ�A�u�����ցv�ƌĂ�A���邢�́u�Ɨ��v�ƌĂ肷��B���͊m���_�I�ȈӖ��ł́A�����ւ����Ɨ��̕������������Ȃ킯�ł��邪�A�Ɨ��Ȃ�Ζ����ւƂȂ邱�Ƃ��킩���Ă���B
�@����ł́A�Ɨ��Ƃ͂ǂ̂悤�ȏ�Ԃ̃N���X�\���Ӗ�����̂ł��낤���B���� x �� y �̗��҂̊ԂɊW���Ȃ��Ƃ�����A�\5.5�Ŏ�����Ă���悤�ȊW������͂��ł���B
�\5.5�@�Ɨ��̏ꍇ�̃N���X�\
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | f11 | f10 | f1� |
| x0 | f01 | f00 | f0� |
| �v | f�1 | f�0 | n |
�@���Ƃ��A���܃J�e�S���[ y1 �̐�߂�䗦�ɒ��ڂ��Ă݂悤�Bx �� y �̗��҂̊ԂɊW���Ȃ���A�J�e�S���[ x1 �̍s�̓x�� f1� �̂����J�e�S���[ y1�̐�߂�䗦���A�J�e�S���[ x0 �̓x�� f0� �̂����J�e�S���[ y1�̐�߂�䗦���������Af�1 /n �̂͂��ł���B�Ȃ��
�@�@�@f11��f1��Ef�1 /n
�@�@�@f01��f0��Ef�1 /n�@�@�@(5.1)
�ƂȂ��Ă���͂��ł���B���l�ɁA�J�e�S���[ y0�̐�߂�䗦�ɒ��ڂ���A
�@�@�@f10��f1��Ef�0 /n
�@�@�@f00��f0��Ef�0 /n�@�@�@(5.2)
�N���X�\�ŁA����(5.1)���܂���(5.2)������������Ƃ��Ax �� y �͓Ɨ�(independent)�ł���ƒ�`����B���̓Ɨ��̒�`�́A�m���̓Ɨ��̊T�O�ƈ�v���Ă���B�Ȃ��Ȃ�A���܊m���̈Ӗ��œƗ��Ƃ���Ȃ�A���Ƃ���(5.1)���̑�1���ɑΉ����āA
�@�@�@Pr (X=x1, Y=y1)
��Pr (X=x1 |Y=y1) Pr (Y=y1)
��Pr (X=x1) Pr(Y=y1)
�ƂȂ邩��ł���B�����ŁA���ӂ� f11 /n�A�E�ӂ� (f1� /n)�E(f�1 /n) �ɑΉ����Ă���̂ŁA����(5.1)���̑�1�������o����邱�ƂɂȂ�B
�@���I�f�[�^�̏ꍇ�ɂ́A�ʓI�f�[�^�̑���(correlation)�̊T�O�ɑΉ�������̂Ƃ��āA�֘A(association)�̊T�O������B�����Ƃ��A���҂̂��āu���ցv�Ƃ������̂ŁA�N���X�\�̏ꍇ�ɂ͊֘A�ƌĂȂ���Ȃ�Ȃ��Ƃ������̂ł͂Ȃ��A���ւƌĂ�ł����܂�Ȃ��B�{���ł͈�т��đ��ւƌĂԂ��Ƃɂ��悤�B
�@���́A�N���X�\�̏ꍇ�ł��A�ʏ�̑��ւƓ��l�̍l����������(��4���Ō�q����悤�ɁA�������W����p���邱�Ƃ�����)�B�s�A�\���̐ϗ����W���̈Ӗ��̐����̍ۂɗp������4�͑�3���̐}4.4�ƑΉ�������Ƃ悭�킩�邪�A
�\5.6�@���S���ւ̏ꍇ�̃N���X�\
(A)���̊��S���ց@�@�@�@�@�@(B)���̊��S����
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | f11 | 0 | f1� |
| x0 | 0 | f00 | f0� |
| �v | f�1 | f�0 | n |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 0 | f10 | f1� |
| x0 | f01 | 0 | f0� |
| �v | f�1 | f�0 | n |
�@�S�����ւ̂Ȃ��Ɨ��ȏꍇ�Ƃ��̋t�Ɋ��S���ւ̏ꍇ�̃N���X�\�͂킩�������A�ʏ�͂��̂悤�ȋɒ[�ȃP�[�X�͊�ł��낤�B���̗��҂̊Ԃ̒��ԓI�ȃN���X�\�̏ꍇ�ɂ́A���ւ̒��x�A���邢�͋t�ɓƗ��ł͂Ȃ����x��\���ɂ͂ǂ�������悢���낤���B����ɂ́A�Ɨ��ł���Ƃ��̏�Ԃ���A�ǂ̒��x�������Ă���̂���\������悢�B
�@���ɁAx �� y �Ƃ��Ɨ��Ƃ���ƁA���̍ۂɊ��҂����x���܂���ғx���́A(5.1)����(5.2)������
�@�@�@f11��f1�f�1 /n�@�@f10��f1�f�0 /n
�@�@�@f01��f0�f�1 /n�@�@f00��f0�f�0 /n
�̂͂��ł���B���̓Ɨ��Ɖ��肵���ꍇ�̊��ғx���Ǝ��ۂ̊ϑ��x���Ƃ̍����傫����Ax �� y �Ƃ��Ɨ��ł͂Ȃ��A�܂葊�ւ��Ă���x���������Ȃ�B�����ŁAO ���ϑ��x��(observed frequency)�AE �����ғx��(expected frequency)�Ƃ���Ƃ��A���̗ʂ��l����̂ł���B
�@�@�@��2������ (O�|E)2/E����i��j ( fij�|fi�f�j /n)2 /(fi�f�j /n)
�����Pearson�̃�2����ʂƌĂ��B�����Ń�2�́u�J�C2��v(chi-square)�ƓǂށB��W�c��2�ϐ� x�Ay ���Ɨ��ł���Ƃ��ɂ́A���̕�W�c����̖���ג��o�W�{�ɂ����邱�̃�2�̕��z���ߎ��I�Ɏ��R�x1�̃�2���z�ɂ����������Ƃ��APearson�ɂ���Ď�����Ă���B
�@���������āA����
�@�@�@H0: �ϐ� x �� y �Ƃ͓Ɨ��ł���B
�����ŏ�����
�@�@�@H0: ���ׂĂ� i, j �ɑ��� fij��fi�f�j /n
�����肷�邽�߂ɂ́A��2��p����悢���ƂɂȂ�B�����Ɨ����̃�2����(��2 test for independence)�Ƃ����B
�@�������A��2�����̂܂ܑ��W���Ƃ��Ďg���ꍇ�ɂ͖�肪����B����́A��2�̂Ƃ肤��l�͈̔͂��A�ʏ�p�����Ă���e��̑��W���̂Ƃ肤��l�͈̔� -1�`1 �ƈ�v���Ȃ��̂ł���B�Ⴆ�N���X�\�̊e�Z���̓x���ɂ���萔 k ���������Ƃ��ɂ́A��2 �̒l��(k)2 �͓����� k �{�ɂȂ��Ă��܂��̂ł���B���ہA
�@�@�@��(k)2����i��j ( kfij�|kfi�kf�j /kn)2 /(kfi�kf�j /kn)��k��2�@�@�@(5.3)
�ƂȂ�B���������āA����Pearson�̃�2����ʂ͕W�{�̑傫�� n �ɔ�Ⴕ�Ă�����ł��傫���Ȃ�A0�`���̒l���Ƃ邱�ƂɂȂ��Ă��܂��B�����ŁA��2�� n �Ŋ����Ă�邱�ƂŁA
�@�@�@��2����2/n
���`���Ă��悢�B����́A���Γx���ɂ��N���X�\�̃�2�����߂��̂Ɠ������ƂɂȂ�B�܂�A
����fij��n�A����fi�f�j ��n2 �ɒ��ӂ���A
�@�@�@��2����(1/n)2����2/n
�@�@�@�@������{ fij2�|2fij fi�f�j /n�{( fi�f�j/n)2}/( fi�f�j)
�@�@�@�@������ fij2 /( fi�f�j)�|����2fij /n�{���� fi�f�j /n2
�@�@�@�@������ fij2/( fi�f�j)�|1�@�@�@(5.4)
�@���o�̉ߒ�������킩��悤�ɁA����(5.4)���́A2�~2�ȊO�̃N���X�\�ɂ��g����B����ɁA2�~2�N���X�\�Ɋւ��ẮA����(5.4)���̕��ꂪ f1�f0�f�1f�0 �ƂȂ�悤�ɒʕ�������ŁA���̕��q�� f11�Af10�Af01�Af00 ��������Ȃ鎮�ɂ��ēW�J����ƁA���̌`�̎���������B
�@�@�@��2��( f11 f00�|f10 f01)2
/( f1� f0� f�1 f�0)�@�@�@(5.5)
�ǂ���̎���p���Čv�Z����ɂ���A���̃�2�̕��������Ƃ��āA
�@�@�@�ӌW��: �Ӂ�(��2/n)1/2
���`����B
�@�ӌW���͂��̒�`��������炩�Ȃ悤�ɁA
�@�@�@�Ӂ�0
�ł���B���ہA(5.5)���̕��q�� f11 f00��f10 f01 �̂Ƃ��A���Ȃ킿�Ax �� y �Ƃ��Ɨ��̂Ƃ��A0���Ƃ�̂ŁA���̂Ƃ� �Ӂ�0 �ƂȂ�B
�@�����A���ӓx�� f1��Af0��Af�1�Af�0 ���Œ肵���Ƃ��A(5.5)���̕��q�́A
�@�Ƃ���ŁA(5.3)������A�e�Z���̑��� n ���傫���Ȃ��Ă���A��2����͗L�ӂɂȂ�₷���Ȃ��Ă��邱�Ƃ��킩��B�o���I�ɂ́An ��400�`500����悤�ȑ傫���ɂȂ�ƁA�����Ȃ�Ƃ����ւ̂��肻����(�܂�A�Ӂ�0�ł͂Ȃ�)�N���X�\�͂قƂ�ǗL�ӂɂȂ��Ă��܂��B���������u�N���X�\�̃�2����� n ���傫���Ƃ��L�ӂɂȂ�₷���v�Ƃ��������́A���͂̍ۂɏ\���m���Ă����K�v������B�������A���̂��Ƃ������Ă��āAn �̑傫�ȃN���X�\�̃�2����͐M�p�ł��Ȃ��Ƃ����l�����邪�A����͐������Ȃ��B�������������́A����A����̍l�����𗝉����Ȃ��܂܂ɁA�u��2����ŗL�ӂȂ�Α��ւ������v�ƒZ���I�ɍl���Ă���l���ׂ�₷������ł���B��1���Ŋ��ɏq�ׂ��悤�ɁA�W�{�̑傫�����\���ɑ傫����A����̐��x���\���Ɍ��サ�Ă���̂ł���B�܂�A��2����̌��ʂ������Ă���Ă���悤�ɁA�Ⴆ�A�Ӂ�0.15 �Ȃ�W�{�ł̒l���u��W�c�ł� �Ӂ�0 �������̂ł͂Ȃ����v�ȂǂƋ^���Ă݂�K�v���A���肵�Ă݂�K�v���A���͂�Ȃ��̂ł���Bn �̑傫�ȃN���X�\�̃�2����͐M�p�ł��Ȃ��̂ł͂Ȃ��A���������K�v�Ȃ��̂��Bn �̑傫�ȃN���X�\�����炱���A�ӂ̒l�͂��Ȃ�̐��x�ŐM�p���ł��邵�A���̂��߂ɁA���肷�邱�Ǝ��̂̈Ӗ����A�K�v���Ȃ��Ȃ��Ă���̂ł���B
�@�\5.7�Ɏ��� s�~t �N���X�\�is��t�j�̂悤�ȏꍇ�ɂ́A���ւ͂ǂ̂悤�ɍl����悢���낤���B
�\5.7�@s�~t �N���X�\
| �@x�@ | y | ||||
|---|---|---|---|---|---|
| �@y1�@ | �@y2�@ | �@�������@ | �@yt�@ | �@�v�@ | |
| x1 | f11 | f12 | �@�������@ | f1t | f1� |
| x2 | f21 | f22 | �@�������@ | f2t | f2� |
| : | : | : | �@�@ | : | : |
| xs | fs1 | fs2 | �@�������@ | fst | fs� |
| �v | f�1 | f�2 | �@�������@ | f�t | n |
�@�ϐ������`�ړx(��1�͑�3���Q�Ƃ̂���)�ɂ����̂ł���A�J�e�S���[�Ԃɉ����ŗL�̏��������݂��Ă���킯�ł͂Ȃ��B����ł��J�e�S���[����̏ꍇ�ɂ́A�ӌW���̂悤�ɑ��W���̕������l���Ȃ��̂ł���Ζ��͂Ȃ��B�Ƃ��낪�A�J�e�S���[��3�ȏ�ɂȂ����ꍇ�ɂ́A�J�e�S���[�̕��ו��͌Œ肵�Ă��Ȃ����ƂɂȂ�B�J�e�S���[��3�̂Ƃ��ł����̕��ו��́A3�̂��̂���3���Ƃ鏇��̌��ł��� 3P3��3�2�1��6 �ʂ�����邱�ƂɂȂ�(��1�͑�5���Q�Ƃ̂���)�B
�@���̂悤�ɁA��ʂ� s�~t �N���X�\�ł́A��̕ϐ��̃J�e�S���[�́A���ꂼ��K�������Œ肵�������ŕ���ł���킯�ł͂Ȃ��̂ŁA�P���ɑ��ւ��l����͓̂���B���������āA���̂ǂ��炩�̕��@���l���邱�ƂɂȂ�B
�@���p�I�ɂ́A1�̕��@�������I�ɗe�Ղɗ������\�ł���A�����Ƃ������͂�����B���������āA�\�Ȃ��1�̕��@���Ƃ邱�Ƃ��]�܂������A���ꂪ�ł��Ȃ��ꍇ������̂ŁA�����ł́A2�̕��@�ɂ��čl���邱�Ƃɂ��悤�B
�@2�~2�N���X�\�Ɠ��l�� s�~t �N���X�\�ł��A�S�����ւ̂Ȃ��ꍇ�Ƃ́A��̕ϐ����Ɨ��ȏꍇ�ł���B���������ēƗ����̌�����l���邱�Ƃ��ł���B�܂�A2�~2�N���X�\�Ɠ��l�� s�~t �N���X�\�ł�Pearson�̃�2����ʂ��v�Z���邱�Ƃ��ł���̂ł���BO ���ϑ��x��(observed frequency)�AE�����ғx��(expected frequency)�Ƃ���ƁAPearson�̃�2����ʂ́A
�@�@�@��2������ (O�|E)2/E����i��j ( fij�|fi�f�j /n)2 /(fi�f�j /n)
�@Pearson�͂��̃�2�̕��z���ߎ��I�Ɏ��R�x (s�|1)(t�|1) �̃�2���z�ɂȂ邱�Ƃ��������B2�~2�N���X�\�̎��R�x��1�ɂȂ邱�Ƃ́A s�~t �N���X�\�̎��R�x (s�|1)(t�|1) �̓���ȏꍇ���Ƃ������Ƃ͗e�Ղɂ킩�邾�낤�B
�@�������A��2��2�~2�N���X�\�̂Ƃ��Ɠ��l�ɁA�W�{�̑傫�� n �ɔ�Ⴕ�āA������ł��傫���Ȃ��Ă��܂��Ƃ�������������̂ŁA��2�𑊊W���Ƃ��Ďg�����Ƃɂ́A2�~2�N���X�\�̂Ƃ��Ɠ��l�̖�肪����B����ł́A2�~2�N���X�\�̂Ƃ��Ɠ��l�ɁA
�@�@�@�Ӂ�(��2/n)1/2
�Œ�`�����ӌW�����g���邾�낤���B���֘A�̂Ƃ��́A��2��0�ɂȂ�̂ŁA�Ӂ�0 �ƂȂ�̂Ŗ��͂Ȃ��B���S���ւ̂Ƃ��͂ǂ����낤���B
�@�����ł܂��A s�~t �N���X�\�ł̊��S���ւ̗���l���Ă݂悤�Bs��t �̂Ƃ��̑�\�I�ȗ�́A�Ίp����̃Z���������x���������A���̃Z�����S�ēx��0�ƂȂ�\5.8�̂悤�ȃN���X�\�ƂȂ�B���̕\5.8�����S���ւ������Ă��邱�Ƃ́A�O�̗͂ʓI�f�[�^�̎U�z�}������[���ł��邾�낤�B���֕\�̏ꍇ�ɂ́A���̊��S���ւƂ����ƁA���̕\5.8�̏ꍇ�Ɍ�����킯�����A����ɁA�J�e�S���[�Ԃɉ����ŗL�̏��������݂��Ă���킯�ł͂Ȃ��Ƃ��ɂ́A���̕\5.8�̕ϐ� x �̃J�e�S���[�̏��������ւ������́A�ϐ� y �̃J�e�S���[�̏��������ւ������̂����S���ւƂȂ��Ă���B���Ȃ킿�A�e�s�A�e��ɂ����āA�x��0�ł͂Ȃ��Z����1�����̂Ƃ��A���S���ւƂ����̂ł���B
�\5.8�@���S�֘A�̃N���X�\�̈��(s��t �̂Ƃ�)
| �@x�@ | y | |||||
|---|---|---|---|---|---|---|
| �@y1�@ | �@y2�@ | �@y3�@ | �@�������@ | �@ys�@ | �@�v�@ | |
| x1 | f11 | 0 | 0 | �@�������@ | 0 | f11 |
| x2 | 0 | f22 | 0 | �@�������@ | 0 | f22 |
| x3 | 0 | 0 | f33 | �@�������@ | 0 | f33 |
| : | : | : | : | �@�@ | : | : |
| xs | 0 | 0 | 0 | �@�������@ | fss | fss |
| �v | f11 | f22 | f33 | �@�������@ | fss | n |
�@�������As��t �̂Ƃ��́A�����P���ɂ͂����Ȃ��B���S���ւƂ́Ay �̒l�����܂�ƁAx �̒l�����܂�Ƃ������Ƃł���ƍl���āA
�\5.9�@���S���ւ̃N���X�\�̈��(s��t �̂Ƃ�)
| �@x�@ | y | ||||
|---|---|---|---|---|---|
| �@y1�@ | �@y2�@ | �@y3�@ | �@y4�@ | �@�v�@ | |
| x1 | f11 | 0 | 0 | 0 | f1� |
| x2 | 0 | f22 | f23 | 0 | f2� |
| x3 | 0 | 0 | 0 | f34 | f3� |
| �v | f�1 | f�2 | f�3 | f�4 | n |
�@���̂Ƃ��A�ӌW�����v�Z����ƁA(5.4)�����g���āA
�@�@�@��2��f112/( f1�f�1)
�{f222/( f2�f�2)
�{f232/( f2�f�3)
�{f342/( f3�f�4)�|1
�@�@�@�@��1�{f22/f2��{f23/f2��{1�|1��2
�ƂȂ�B��ʓI�ɁAs�~t �N���X�\(s��t)�̃�2�̒l�́A���S���ւ̂Ƃ���1�ł͂Ȃ� s�|1 �ƂȂ�̂ł���B�����ŁA���S���ւ̂Ƃ���1�̒l���Ƃ�悤�ɁA���̂悤�ȌW�����l����B
�@�@�@V��{��2/(s�|1)}1/2�@�@�@s��t
����́A�N���}�[�� V �W��(Cramer's V)�ƌĂ����̂ŁA����܂ł̂��Ƃ�����킩��悤�ɁA
�@�@�@0��V��1
�Ƃ����A���W���Ƃ��Ăӂ��킵�������������Ă���B2�~t �N���X�\�̂Ƃ�
�@�@�@V����
�Ƃ�������������A�������A2�~2�N���X�\�̂Ƃ����A���W���͈�v����̂ŁA2�~2�N���X�\�̂Ƃ����܂߂āA��ʂɃN���X�\�̑��W���Ƃ��ẮA����I�ɃN���}�[�� V �W����p����悤�ɂ��Ă����Ƃ悢�B(�\5.2(B)�ŁAV��-0.17 �ƕ��̒l�������Ă��闝�R�ɂ��ẮA��5��(2)���Q�Ƃ̂��ƁB)
�@����2�~2�N���X�\�ɑ��Ă��s�A�\���̐ϗ����W����K�p���邱�Ƃ��ł���B�l�����Ƃ��ẮA2�l���I�f�[�^�Ƃ��Ĉ������Ƃ����̂ł���B�����ł��ܕ\5.10�̂悤�ɁA����̃J�e�S���[��0�A�����̃J�e�S���[��1�Ƃ������l��^���A�s�A�\���̐ϗ����W����K�p���Ă݂悤�B
�\5.10�@2�~2�N���X�\
| �@x�@ | y | ||
|---|---|---|---|
| �@1�@ | �@0�@ | �@�v�@ | |
| 1 | f11 | f10 | f1� |
| 0 | f01 | f00 | f0� |
| �v | f�1 | f�0 | n |
�@�@�@x��f1�/n
�@�@�@y��f�1/n
�@�@�@sx2��(1�|f1�/n) f1�/n��( f0�/n)( f1�/n)
�@�@�@sy2��(1�|f�1/n) f�1/n��( f�0/n)( f�1/n)
�@�@�@sxy���� xi yi /n�|x�y��f11/n�|x�y��f11/n�|( f1�/n)( f�1/n)
�ł��邩��
�@�@�@rxy��sxy/sxsy
�@�@�@�@��{ f11/n�|( f1�/n)( f�1/n)}
/{( f0�/n)( f1�/n)( f�0/n)( f�1/n)}1/2
�@�@�@�@��(nf11�|f1�f�1)
/( f0� f1� f�0 f�1)1/2
�@�@�@�@��{( f11�{f10�{f01�{f00) f11�|( f11�{f10)( f01�{f11)}
/( f0� f1� f�0 f�1)1/2
�@�@�@�@��( f11 f00�|f10 f01)
/( f0� f1� f�0 f�1)1/2�@�@�@(5.6)
����2���(5.5)���̃�2�ƈ�v����̂ŁA
�@�@�@rxy2����2��V2
�@2�~2�N���X�\���Ȃ킿�l���\�ɑ��ēK�p�����s�A�\���̐ϗ����W���́A�l���_���W��(four-fold point correlation coefficient)�A�����āA�_���W��(point correlation coefficient)�A���邢�͎l���ϗ����W���܂��͎l���\�ɑ���s�A�\���̑��W���Ƃ����邱�Ƃ�����B
�@�s�A�\���̐ϗ����W�� rxy �̐�Βl�͗��ϐ��̐���1���ϊ��ɂ���ĕς��Ȃ�(���W���̐���2)�̂ŁA��̃J�e�S���[�����l�f�[�^�Ƃ��ė^�����Ă���������A���̂悤�� rxy2����2 �Ƃ����W�͕ۏ����B
�@2�~2�N���X�\�̏ꍇ�ɂ́A����ɁA�P���h�[���̏��ʑ��W����b(Kendall's ��b)�Ƃ̊ԂɁA��b��rxy �Ƃ����W������B���܃P���h�[���̏��ʑ��W���̍l�������N���X�\�ɂ��̂܂ܓK�p���Ă݂悤�B
�@�@�@��A��f11 f00
�@�@�@��B��f01 f10
����ɁA��C �ɂ��čl���Ă݂悤�B�����Z���ɑ������̌�(�ϑ��l)�̂���́Ax �ɂ��Ă� y �ɂ��Ă������ʂȂ̂ŁA�e�Z�� (i, j) �ɑ����� fij �̌̂̂��ׂĂ̑g�ݍ��킹
�@�@�@fijC2��fij ( fij�|1)/2
�ʂ�̑͂��ׂē����ʂƂȂ�B�܂��Z�� (1, 1) �� (1, 0) �ɑ�����̊Ԃ̑� f11�Ef10 �ʂ�� x �ɂ��ē����ʂł��邵�A�Z�� (0, 1) �� (0, 0) �ɑ�����̊Ԃ̑� f01�Ef00 �ʂ�� x �ɂ��ē����ʂł���B�����������Ƃ���A
�@�@�@��C��f11( f11�|1)/2�{f10( f10�|1)/2�{f01( f01�|1)/2�{f00( f00�|1)/2�{f11 f10�{f01 f00
�@�@�@2��C��f112�{2f11 f10�{f102�{f012�{2f01 f00�{f002�|f11�|f10�|f01�|f00
�@�@�@�@�@��( f11�{f10)2�{( f01�{f00)2�|n
�@�@�@�@�@��f1�2�{f0�2�|n
����āA
�@�@�@n(n�|1)�|2��C��n(n�|1)�|( f1�2�{f0�2�|n)��n2�|f1�2�|f0�2��( f1��{f0�)2�|f1�2�|f0�2��2f1� f0�
���l�ɂ��āA��D�ɂ��Ă��A
�@�@�@��D��f11( f11�|1)/2�{f10( f10�|1)/2�{f01( f01�|1)/2�{f00( f00�|1)/2�{f11 f01�{f10 f00
�@�@�@n(n�|1)�|2��D��2f�1 f�0
���������āA��b �̒�`��(5.6)������A
�@�@�@��b��( f11 f00�|f10 f01) /( f0� f1� f�0 f�1)1/2��rxy
�@���̂悤�ɁA2�~2�N���X�\�ł́A�s�A�\���̐ϗ����W����P���h�[���̏��ʑ��W����K�p���Ă��A���̐�Βl�̓ӌW�������ā@V �W���Ɉ�v����B�܂�A2�~2�N���X�\�ɂ��ẮA���ւ̑傫���𑪂邱�Ƃɂ��ẮA�����̑��W���̊Ԃň�v�������Ă���B
���)�@�\5.11��9����2�~2�N���X�\�̑��W���Ƃ��� V �W�������߂�B(V���ӁAV2����2��r2����b2�Ar����b �ɒ���)
�\5.11�@�l�X�ȑ��W����2�~2�N���X�\
(1) V���@�@�@�@�@�@�@�@�@�@(2) V���@�@�@�@�@�@�@�@�@�@(3) V��
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 55 | 45 | 100 |
| x0 | 45 | 55 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 60 | 40 | 100 |
| x0 | 40 | 60 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 65 | 35 | 100 |
| x0 | 35 | 65 | 100 |
| �v | 100 | 100 | 200 |
(4) V���@�@�@�@�@�@�@�@�@�@(5) V���@�@�@�@�@�@�@�@�@�@(6) V��
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 70 | 30 | 100 |
| x0 | 30 | 70 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 75 | 25 | 100 |
| x0 | 25 | 75 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 80 | 20 | 100 |
| x0 | 20 | 80 | 100 |
| �v | 100 | 100 | 200 |
(7) V���@�@�@�@�@�@�@�@�@�@(8) V���@�@�@�@�@�@�@�@�@�@(9) V��
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 85 | 15 | 100 |
| x0 | 15 | 85 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 90 | 10 | 100 |
| x0 | 10 | 90 | 100 |
| �v | 100 | 100 | 200 |
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | 95 | 5 | 100 |
| x0 | 5 | 95 | 100 |
| �v | 100 | 100 | 200 |
�s�t�@�܂��AV��0 (�Ɨ�)�̂Ƃ��̊��ғx�������߂Ă݂悤�B9���̃N���X�\�͂��ׂē������ӓx���Ȃ̂ŁA���ғx���������ɂȂ�A�\5.12(A)�Ɏ����悤�Ȋ��ғx���ɂȂ�B�܂�A�ǂ̃Z���ɂ������x��50�����邱�ƂɂȂ�̂ŁA����� a �ƒu�����Ƃɂ��悤�B����ƁA����9���̃N���X�\�ɂ���ϑ��x���́A�\5.12(B)�̂悤�ɕ\�����邱�Ƃ��ł���B
�\5.12�@���ғx���Ɗϑ��x��
(A)V��0 (�Ɨ�)�̂Ƃ��̊��ғx��(a��50)
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | a | a | 2a |
| x0 | a | a | 2a |
| �v | 2a | 2a | 4a |
(B)�N���X�\(1)�`(9)�ɂ���ϑ��x��(a��50)
| �@x�@ | y | ||
|---|---|---|---|
| �@y1�@ | �@y0�@ | �@�v�@ | |
| x1 | a�{b | a�|b | 2a |
| x0 | a�|b | a�{b | 2a |
| �v | 2a | 2a | 4a |
9���̃N���X�\�̂��̐������g���āA9���̃N���X�\�̑��W�����܂Ƃ߂Čv�Z���Ă��܂����B
�@�@�@��2��b2/a�{b2/a�{b2/a�{b2/a��4b2/a�@����܂ŏq�ׂĂ����悤�ȃN���X�\���쐬���A�Ɨ����̃�2����Ƃu�W���Ȃǂ̑��W�������߂邱�Ƃ́ASAS���g���Δ��ɊȒP�ɂł���B����ɂ́A��2�͑�6���ŒP���W�v������ۂɗp����FREQ�v���V�W����TABLES�����̕ϐ��̎w��̎d����ς��邾���ł悢�B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC FREQ DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; TABLES �ϐ����X�g*�ϐ����X�g/CHISQ;�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I1*V2/CHISQ; �@�@�@OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC FREQ DATA=�i�vSAS�f�[�^�Z�b�g��; TABLES �ϐ����X�g*�ϐ����X�g/CHISQ;�@�@�@�@�@�@�@�@�@ [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I1*V2/CHISQ; �@�@�@OPTIONS NOCENTER; RUN; |
��͂�PC��SAS�̃v���O������1�s�ڂ��폜����ƁA�`���I�ɂ�CMS��SAS�̃v���O�����Ɠ����ɂȂ�B
�@�Ɨ����̃�2����� V�W���Ȃǂ̑��W�������߂邽�߂ɁATABLES���̃I�v�V�����Ƃ��āA�����ł� /CHISQ ���w�肵�Ă��邪�A��ŐG���悤�ɂ���ɐF�X�ȃI�v�V������lj��w�肷�邱�Ƃ��ł���B
�@��ʂɁATABLES���Łu�ϐ�1*�ϐ�2�v�Ǝw�肷��ƁA�\5.13�̌`���̃N���X�\�������B
�\5.13�@TABLES���Łu�ϐ�1*�ϐ�2�v�Ǝw�肵���Ƃ��쐬�����N���X�\�̈�ʌ`��

����ɁATABLES���Łu�ϐ����X�g*�ϐ����X�g�v���w�肷��ƁA�u*�v���͂���łł���ϐ��̑g�������ׂĂɂ��ăN���X�\�������B�Ⴆ�A
| �@�@�@TABLES (A B)*C; | �́@TABLES A*C B*C; | �Ǝw�肵���̂Ɠ������� |
| �@�@�@TABLES (A B)*(C D); | �́@TABLES A*C B*C A*D B*D; | �Ǝw�肵���̂Ɠ������� |
�@�v���O����������s����ƁA�\5.14�̂悤�ȃN���X�\���쐬�����͂��ł���B�������A���ۂɂ́A���̃N���X�\���f�B�X�v���C��ʂŌ��邱�Ƃ͂ł��Ȃ��B�����OUTPUT�E�B���h�E�ɏo�͂��ꂽ���̂��t�@�C���Ɉ�U�ۑ����Ă���A�M�҂��ҏW���ĂȂ����킹�����̂ł���B
�\5.14�@�v���O������ō쐬�����N���X�\
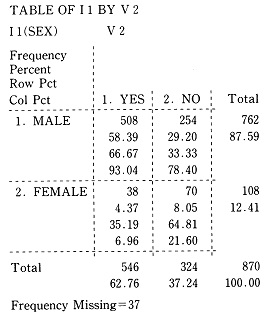
��) �������A�f�B�X�v���C��ʂł́A���̃N���X�\��1�s���ɕ��������OUTPUT�E�B���h�E�ɕ\�������B
�@�ꉞ�A���̌`���̃N���X�\�ɂ��ĉ�����Ă����ƁA���̃N���X�\�ł͊e�Z���ɕ\������Ă��鐔�l�́A�N���X�\�̍���ɕ\������Ă���Ƃ���A
| �@�@�@Frequency | �������x�� |
| �@�@�@Percent | ���������Γx�� |
| �@�@�@Row Pct | �������s���Γx�� |
| �@�@�@Col Pct | �������Γx�� |
�@�����ŁATABLES���ŁA�K�v�ł͂Ȃ����̂�\�������Ȃ����̂悤�ȃI�v�V�������g�����ƂɂȂ�B
| �@�@�@NOFREQ | �������x����\�����Ȃ� |
| �@�@�@NOPERCENT | ���������Γx����\�����Ȃ� |
| �@�@�@NOROW | �������s���Γx����\�����Ȃ� |
| �@�@�@NOCOL | �������Γx����\�����Ȃ� |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I1*V2 �@�@�@/CHISQ NOPERCENT NOCOL; �@�@�@OPTIONS NOCENTER; RUN; |
�}5.1�@SAS�ɂ��N���X�\
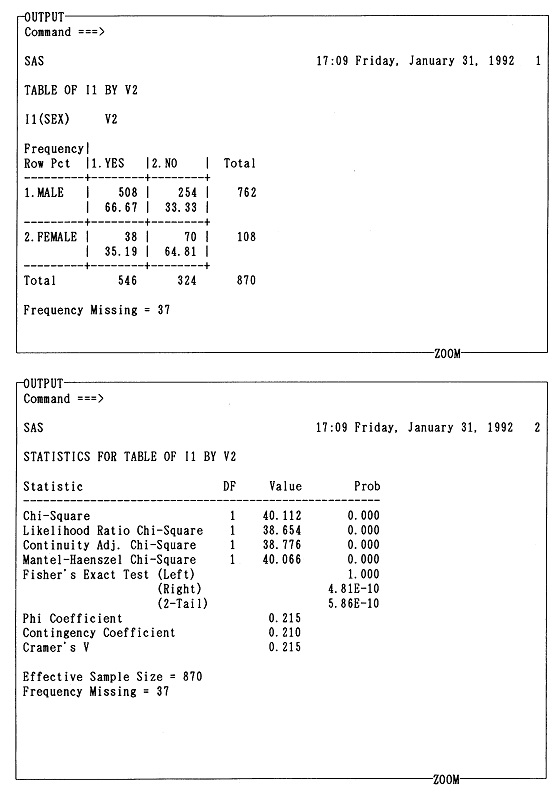
�@���̏ꍇ�A2�~2�N���X�\�Ȃ̂ŁA�N���}�[�� V �W��(Cramer's V)�ƃӌW��(Phi Coefficient)�͂Ƃ���0.215�œ������B��2 (Chi-Square)�͎��R�x(DF) 1�ŁA���̒l(Value)��40.112�ƂȂ�B�Ɨ����̃�2����̗L�ӊm��(Prob)��0.000�A�܂�A�L�Ӑ�����0.1%�ɐݒ肵�Ă���ꍇ�ł��A�L�ӂł���A�Ɨ����̉����͊��p���ꂽ���ƂɂȂ�B
�@�܂��I�v�V�����Ƃ���CHISQ���w�肵�Ă���Ƃ��́A����ɒlj��I�ɁA���̂悤�ȃI�v�V�������w�肵�āA�N���X�\�̃Z�����ɕ\�������邱�Ƃ��ł���B
| �@�@�@EXPECTED | �������u���ғx���v��\������ |
| �@�@�@DEVIATION | �������u�x���|���ғx���v��\������ |
| �@�@�@CELLCHI2 | �������u(�x���|���ғx��)2/���ғx���v��\������ |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES I1*V2 �@�@�@/CHISQ NOPERCENT NOCOL DEVIATION; �@�@�@OPTIONS NOCENTER; RUN; |
�@�����Œ��ӂ��K�v�Ȃ̂́ASAS�ł�2�~2�N���X�\�̏ꍇ�Ɍ����āA�u�ӌW���v�uV �W���v�ł����̑��ւ��������ꍇ�ɂ́A���̒l���Ƃ�悤�ɂȂ��Ă���Ƃ������Ƃł���B���̈Ӗ��ł́A���̃s�A�\���̐ϗ����W�����o�͂���悤�ɂȂ��Ă���Ƃ�������B�������A2�~2�ȊO�̃N���X�\�ł́A�{���̒�`��p���āA���̒l�����o�͂���Ȃ��B�{���̃ӌW���AV �W���̒�`��w�i�ƂȂ�l�������炵�āA���̒l���Ƃ邱�Ƃ͊Ԉ���Ă��邪�A���[�U�[�Ƃ��ẮA���̂��Ƃ�m������ŁA2�~2�N���X�W�v�\�̏ꍇ�A�o�͂����u�ӌW���v�uV �W���v�̒l�����̂܂g�����A���邢�͐�Βl���g���������߂�Ηǂ��B���̏͂ł́ASAS�̎��s���ʂƂ̑Ή������邽�߂ɁA�o�͂��ꂽ���l�̒l�ł����̂܂g���Ă���B
�@�Ƃ���ŁA�ϐ��̐��������Ă���ƁA�N���X�\��1��1�����Ă����̂͑�ςȍ�ƂɂȂ��Ă���B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́AYes-No�`����75�ϐ��ׂĂ��邪(�ڂ�������6���̎����Q��)�A�ߋ��ɍs���Ă��������ł���������100�ϐ��O��̒������s���Ă��Ă���B����100�ϐ��̃f�[�^�ł������Ƃ���ƁA����������ł́A100�~100��10,000���B���̂����A�����ϐ����m�̃N���X�\100���͌���K�v���Ȃ����A�����ϐ��̑g�ݍ����̃N���X�\��2�����܂܂�Ă���̂ŁA�����͂ǂ��炩�����������悢���Ƃɂ��Ă��A�Ȃ�� (10,000-100)/2��4,950���A����5,000�������Ȃ��Ă͂Ȃ�Ȃ��v�Z�ɂȂ�B���C���t���[���ł���A���̒��x�̏W�v��Ƃ������Ă������Ƃ����ԂɌ��ʂ��o�͂���Ă���B���Ȃ̂́A�����ǂސl�Ԃ̔\�͂̕��Ɍ��E������Ƃ������Ƃł���B�܂��Ɍ��肳�ꂽ�������ł���B����Ă݂�����ɂ킩�邱�Ƃ����A�����ɑi����2�~2�N���X�\�ł�100���ǂނ̂͑�ςȍ�Ƃł���B��ʂ� s�~t �N���X�\�ł�1��1���̃N���X�\�̉�ǂɎ��Ԃ�������A��]�I�ȍ�ƂɂȂ�B���C���v�����^�[�ɏo�͂����ꍇ�A�ʏ�A�p��1�y�[�W��1���̃N���X�\����������̂ŁA��5,000���Ƃ������Ƃ́A���Ƀ��C���v�����^�[�p���̒i�{�[����2�`3�����ɑ������邱�ƂɂȂ�B���̒m��͈͂ŁA���ꂾ���̗ʂ̃N���X�\�̎R��ǂ݂��Ȃ����l�Ԃ͑��݂��Ȃ��B�����������C���v�����^�[�p�����߂��邾���ŁA�r���ؓ��ɂɂȂ��Ă��܂��B���e�𗝉�����Ȃǂ��͂�s�\�ł���B�������A������ŕϐ��Ԃ̊W������ł������Ƃ́A���͂ɍۂ��ďd�v�Ȃ��ƂȂ̂ł���B
�@����ł́A�M�҂͂ǂ̂悤�ɂ��Ă����̂ł��낤���B�����
�@CORR�v���V�W�����g���APC��SAS�̃v���O������ł����ƁA
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC CORR NOSIMPLE DATA=SAVE.JPC; �@�@�@VAR TII1 -TII7; �@�@�@WITH TII1 -TII3; �@�@�@OPTIONS NOCENTER; RUN; |
�}5.2�@SAS�ɂ��N���X�\�̑��W���s��
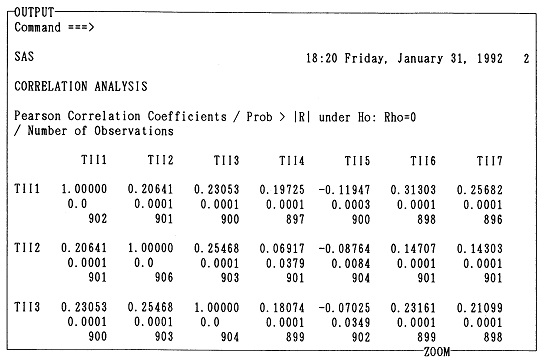
�@���̐}5.2�̂悤��SAS�ɂ���ďo�͂��ꂽ�N���X�\�̑��W���s��́A���̂܂܂ł͎g��Ȃ��B����OUTPUT�E�B���h�E����U�t�@�C���ɕۑ����Ă���A���̃t�@�C����ҏW���āA�\�Ƃ��Ă̌`���𐮂��āA�\5.15�̂悤�ȕ\���쐬����̂ł���B�����ŁA�L�ӊm���͐����̂܂܂ł́A���o�I�Ƀs���Ƃ��Ȃ��̂ŁA�L�������Ă����ƂƂ��ɁA�e�ϐ��ɂ���6�͎���D�̓��̓t�H�[�}�b�g�ɂ���ϐ����x�����g���āA�ȒP�ȓ��e���������Ă����B
�\5.15�@�N���X�\�̑��W���ɂ��܂Ƃ߂̗�
| II1. ��Ɏd�� ���P�S�| |
II2. ���ɍS �炸�d�� |
II3. ���E�ɍS �炸�d�� |
II4. �������� �ł��ʗp |
II5. ��i�ɑf ���ɏ]�� |
II6. �o�c���j �l���d�� |
II7. ��i���� �����Ϗ� | |
|---|---|---|---|---|---|---|---|
| II1. ��Ɏd�� ���P�S�| | 1.00000 902*** | 0.20641 901*** | 0.23053 900*** | 0.19725 897*** | -0.11947 900*** | 0.31303 898*** | 0.25682 896*** |
| II2. ���ɍS �炸�d�� | 0.20641 901*** | 1.00000 906*** | 0.25468 903*** | 0.06917 901* | -0.08764 904** | 0.14707 901*** | 0.14303 901*** |
| II3. ���E�ɍS �炸�d�� | 0.23053 900*** | 0.25468 903*** | 1.00000 904*** | 0.18074 899*** | -0.07025 902* | 0.23161 899*** | 0.21099 898*** |
�@�܂��Ⴉ��n�߂悤�B���܁u�g�D�������̂��߂̏]�ƈ��ӎ������v�Œ��ׂ����̓��Yes-No�`���̎���ɑ���̃N���X�\������Ă݂悤�B
| �@�@ | IV7. | �w�����o����Ă��A���߂����Ă��邤���ɁA���������ɂȂ邱�Ƃ�����B | 1. Yes�@2. No |
| �@�@ | VI7. | ���������ʂ͏[�����Ă���B | 1. Yes�@2. No |
�\5.16�@�w���̂��߂����ƕ��������̃N���X�\
| IV7 �w����� �߂����� | VI7�@���������ʂ͏[�� | ||
|---|---|---|---|
| 1. Yes | 2. No | �@�v�@ | |
| 1. Yes | 267 (45.56) | 319 (54.44) | 586 �@ |
| 2. No | 205 (68.56) | 94 (31.44) | 299 �@ |
| �v | 472 | 413 | 885 |
�@�����������ϐ��Ƃ̔�r�ƕ\5.16�Ƃ��ӂ܂���A���̃N���X�\�̎�������X���͖��炩�ł���B�܂�A�w���̂��߂������ł��Ȃ��Ƃ���ł͕��������ʂ��[�����Ă��邵�A�t�ɁA�w���̂��߂������ł���Ƃ���ł͕��������ʂ��[�����Ă��Ȃ��Ƃ����̂ł���B������885�l������ƁA��2����͗L�ӂɂȂ�₷���̂͊m�������A�\5.16�̃N���X�\�����Ă��A���̌X���͂͂����肵�Ă���B�v����ɁA���������ʂ��������肵�Ă���Ƃ���́A�w�����������肵�Ă���Ƃ������ƂȂ̂����c�c�B
�@���������A�ǂ����펯�I�ɔ[���ł��Ȃ��A�����̂͂����肵�Ȃ��������ʂ��ł��ꍇ�A���ꂼ���������Ǝ�����Ŋ�Ԃ̂͂܂������B���������͉������ɁA�������Ƃ��炵�����R��������̂ŁA���������펯�I�ȉ\��������݂Ԃ��ɂ��Ă݂�܂ł͌��_�͏o���Ȃ��B
�@�����Ŏ����ɁA�����Ώۊ�Ƃ����v���ƊW�Ƃ���ȊO�̗��ʋƂȂǂɕ�������ŁA�ʁX�ɃN���X�\������Ă݂�ƁA�\5.17�̂悤�ɂȂ����B�܂��ǂ���̃N���X�\���L�ӂȕ��̑��֊W�����邪�A���W���ł���N���}�[�� V �͐����Ə������Ȃ����B�܂�A�w���̂��߂����ƕ��������ʂł̏[���Ƃ̑��ւ͐����Ə������Ȃ��Ă���B�������A�\5.17�̃N���X�\���悭����ƁA����v���Ƃł́A�w���̂��߂����������A���������ʂł͂܂��[�����Ă��Ȃ��Ƃ������Ƃ��킩��B����ɑ��āA���v���Ƃł́A���������ʂ͏[�����Ă��邵�A�w���̂��߂���������v���Ƃɔ�ׂ�Ώ��Ȃ��Ȃ��Ă���Ƃ������Ƃ��킩��B
�\5.17�@�w���̂��߂����ƕ��������̃N���X�\
(A)���v���Ɓ@�@�@�@�@�@�@�@�@�@�@(B)����v����
| IV7 �w����� �߂����� | VI7�@���������ʂ͏[�� | ||
|---|---|---|---|
| 1. Yes | 2. No | �@�v�@ | |
| 1. Yes | 223 (66.57) | 112 (33.43) | 335 �@ |
| 2. No | 187 (76.95) | 56 (23.05) | 243 �@ |
| �v | 410 | 168 | 578 |
| IV7 �w����� �߂����� | VI7�@���������ʂ͏[�� | ||
|---|---|---|---|
| 1. Yes | 2. No | �@�v�@ | |
| 1. Yes | 44 (17.53) | 207 (82.47) | 251 �@ |
| 2. No | 18 (32.14) | 38 (67.86) | 56 �@ |
| �v | 62 | 245 | 307 |
�@�\5.16�Ɍ����鍂�����ւ́A���̂悤�ɐ����̈قȂ�2�Q�A���v���ƂƔ���v���ƂƂ����킹�ďW�v�������߂ɏo���������̂ƍl����ꂻ���ł���B�펯�I�ɍl���Ă݂�ƁA����Ȑݔ���u���Ǘ��^�p���Ă�����v���ƂŁA�w���̂��߂��������Ȃ��͓̂��R�ł��邵�A�Ɛ��n��Ɛ��O��Ƃ��Ă�����v���Ƃ����������ʂ��[��������]�T������Ƃ����̂��܂����R��������Ȃ��B����ƂĂ܂������̈���o�Ȃ��킯�ŁA�t�H���[�E�A�b�v�E�q�A�����O��ǎ���K�v�Ƃ��Ă͂��邪�A�w���̂��߂����ƕ��������Ƃ������ړI�ɂ͖{�����W�Ȃ͂��̕ϐ����A���͂Ƃ��Ɋ�Ƃ̋Ǝ�A�ƑԁA�s����ȂǂƂ͖��ڂɌ��ѕt���Ă��������Ƃ������Ƃ́A���̕\5.17�ł��\���Ɏ�����Ă���Ƃ����邾�낤�B
�@���܂̕��͂́A���߂����ƕ��������Ƃ���2�ϐ��̃N���X�\�ɁA����ɑ�3�̕ϐ��Ƃ��Ĉ��́u�Ǝ�v�����čs�Ȃ������̂ł���B���̂悤�ɁA����܂łɈ����Ă����悤��2�ϐ��̃N���X�\�ɁA����ɑ�3�̕ϐ������āA�ϐ��Ԃ̊W�𖾂炩�ɂ��Ă������@����ʂɁA�G���{���C�V����(elaboration)�ƌĂԁB����̓I�ɂ����A�m�F�������Ǝv���Ă���Ɨ��ϐ�x�Ə]���ϐ�y�Ƃ̊Ԃ̊֘A�������N���X�\�ɁA��3�̕ϐ� t �����āA3�d�N���X�\���쐬����̂ł���B���̂Ƃ��̑�3�ϐ� t �̃J�e�S���[(t1, t2, ...)���Ƃɍ��ꂽ x �� y �̃N���X�\�̑��ւ�����(split correlation)�A�܂��́A��������(conditional correlation)�A�w�ʑ���(stratified correlation)�ƌĂԂ��A���̕������ւׂ邱�ƂŁA�ϐ��Ԃ̊W�����炩�ɂ����̂ł���B
�@����(1)�̕\5.16�A�\5.17�Ŏ������悤�ȃP�[�X�A�ɒ[�ɂ� x �� y �Ƃ̊Ԃɂ͑��ւ�������̂ɁA�������ւ��S���Ȃ��\5.18�̂悤�ȃP�[�X�͉����Ӗ����Ă���̂��낤���B����ɂ͎��̓�̉\�����l������B
�\5.18�@�ɒ[�ɂ����ˋ��
�@(A)���v���Ɓ{(B)����v���Ɓ�(C)�S��
| IV7 | VI7 | ||
|---|---|---|---|
| Yes | No | �v | |
| Yes | 9 | 1 | 10 |
| No | 81 | 9 | 90 |
| �v | 90 | 10 | 100 |
| IV7 | VI7 | ||
|---|---|---|---|
| Yes | No | �v | |
| Yes | 9 | 81 | 90 |
| No | 1 | 9 | 10 |
| �v | 10 | 90 | 100 |
| IV7 | VI7 | ||
|---|---|---|---|
| Yes | No | �v | |
| Yes | 18 | 82 | 100 |
| No | 82 | 18 | 100 |
| �v | 10 | 100 | 200 |
| Cramer's V��0�@ | Cramer's V��0�@ | Cramer's V��-0.64 |
| ��2��0 | ��2��0 | ��2��81.92*** |
�@����́A��3�̕ϐ� t �� x �� y �ɑ����s�ϐ�(antecedent variable)�ɂȂ��Ă���ꍇ�ł���B�}��������A
�@�@�@x �� t �� y
�Ƃ������ƂɂȂ�A�^������(spurious correlation)��������邱�ƂɂȂ�B�^�����ւƂ́A x �� y �ɂ͈��ʊW�����݂����A���ہAx ��l�דI�ɕω������Ă� y �ɕω��͐����Ȃ��B�����قǂ�(1)�̗�����̋^�����ւɑ�������B�܂�A�u�����������[��������ƁA�w���̂��߂�������������悤�Ɍ����邯��ǂ��A���́A����͑啔�����A�w�Ǝ�x�Ƃ�����s�ϐ������邽�߂̌�������̋^�����ւł���Ɛ��������v�̂ł���B���������āA���̒������ʂ���A�w���̂��߂��������炷���߂ɂ́A�����������[��������悢�̂��ƁA�Z���I�ɍl����l�������(����Ȑl�͂��Ȃ��Ǝv����)�A���̐l�͌�������̋^�����ւɘf�킳��āA�^�̈��ʊW�����߂������Ƃ������ƂɂȂ�B
�@�������A���̂悤�� x �� y �Ƃ̊Ԃɂ͑��ւ�������̂ɁA�������ւ��Ȃ��ꍇ�ɂ͂�����ʂ̎��̂悤�ȉ\�����l������̂Œ��ӂ�����B
�@����́A��3�̕ϐ� t ���Ax �� y �Ƃ̊Ԃ̔}��ϐ�(intervening variable)�ɂȂ��Ă���ꍇ�ŁA�}��������Ǝ��̂悤�ɂȂ�B
�@�@�@x �� t �� y
�ԐړI�Ȉ��ʊW�����ڂ������߂������̂ł���B���������̏ꍇ�ɂ́A���ړI�ɂ͈��ʊW���Ȃ��Ƃ͂����A�ԐړI�ɂ͈��ʊW������̂ŁA�����������̋^�����ւƂ͈قȂ�B
�@�������A(a)�̃^�C�v�ɂȂ邩�A(b)�̃^�C�v�ɂȂ邩�A�܂���ʊW�̖��̕������ǂ��Ȃ邩�͏펯��w��I�~�ϓ������āA�v�l�����ɂ���čs���ȊO�ɂ͂Ȃ��B�܂�A����͓��v������̖��ł͂Ȃ��A�_���̖��ł���B
�@�Ō�ɁA(a)(b)�Ƃ͋t�̃P�[�X�Ƃ��āA����(c)������̂ł����Ă������B
�@���Ƃ� x �� y �Ƃ̑��ւ� t1 �� t2 �Ƃɂ���Ē��x���قȂ��Ă��邱�Ƃ����������ꍇ�ł���B�ɒ[�ȏꍇ�ɂ́A�S�̂̒P�����ւ�0�ł��邪�A���ꂪ���́A������������̓�̕������ւ̍����̕\�ʓI���ʂł��������Ƃ������Ă���B�܂�A�^��������(spurious non-correlation)�ł���B�^�������ւ̏ꍇ�ɂ́A�S�̂ł͖����ւł����Ă��A���ۂɂ͓K���ɃO���[�v���A�w�ʉ�(stratification)���s�����ƂŁA�e�O���[�v���ł̑��ւm�Ɏ������Ƃ��ł���B
�@3�d�N���X�\���쐬���AV �W���̂悤�ȑ��W�������߂邱�Ƃ́ASAS��FREQ�v���V�W�����g���Δ��ɊȒP�ɂł���B
| PC��SAS |
|---|
|
LIBNAME libname '���p�X��'; PROC FREQ DATA=libname.�i�vSAS�f�[�^�E�Z�b�g���{��; TABLES �ϐ�1*�ϐ�2*�ϐ�3�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [/�I�v�V����]; [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
LIBNAME SAVE '��MYDIR'; PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES KCODE*IV7*VI7 �@�@�@/CHISQ NOPERCENT NOCOL; OPTIONS NOCENTER; RUN; |
| CMS��SAS |
|---|
|
PROC FREQ DATA=libname.�i�vSAS�f�[�^�E�Z�b�g��; TABLES �ϐ�1*�ϐ�2*�ϐ�3�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [/�I�v�V����]; [OPTIONS NOCENTER;] RUN; |
| ��) |
|---|
|
PROC FREQ DATA=SAVE.JPC; �@�@�@TABLES KCODE*IV7*VI7 �@�@�@/CHISQ NOPERCENT NOCOL; OPTIONS NOCENTER; RUN; |
�@CMS��SAS�̃v���O������́A�`���I��PC��SAS�̃v���O�������1�s�ڂ��폜�������̂ɂȂ�B���̃v���O�����ɂ���āA�ϐ�1�̊e�J�e�S���[���ƂɁA�ϐ�2*�ϐ�3�̃N���X�\������邱�ƂɂȂ�B�������A�S�̂̃N���X�\�͂���ł͍���Ȃ��̂ŁA�ʂɍ��K�v������B(�����K���5.1)
5.1 �G���{���C�V���� �@��2���ŕ\5.2�̃N���X�\���쐬����Ƃ��Ɏg�p��������V2�Ǝ���V12�Ƃ̊ԂŃN���X�\���쐬����ƂƂ��ɁA��3�̕ϐ��Ƃ��āA���ʂɊւ��鎿��I1��p����3�d�N���X�\���쐬����Ǝ��̂悤�ɂȂ����B����SAS�̏o��(�ꕔ�ȗ�)���ǂ̂悤�ɗ����ł��邩���q�ׂ�B
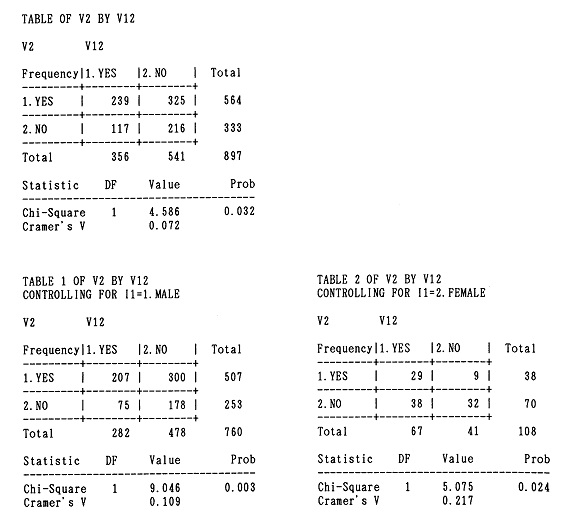
5.2�@�^�������� �@�S�̂̑��ւ�0�ł��邪�A���ꂪ���́A������������̓�̕������ւ̍����̕\�ʓI���ʂł������Ƃ����悤�ȋ^�������ւ̂����Ƃ��炵���ˋ����l���A�\5.16�A�\5.17�A�\5.18���Q�l�ɂ��ăN���X�\���쐬����B
�@�{���ł́A���v�����̎��ۂ̎p���ł��邾����̓I�����m�ɃC���[�W���Ă��炤���߂ɁA���v�����A���͂ɗp����f�[�^����͂��߁ASAS�v���O�����̗�Ȃǂ��A��т��āu�g�D�������̂��߂̏]�ƈ��ӎ������v��f�ނƂ��Ă���B���̒����菇�ƕ��@���A���ۂɗp����ꂽ�ڍׂȎ����ƂƂ��Ɏ��グ�悤�B�����Ƃ��A���̏͂͒P�ɋ�̗�����Ƃ��������ł͂Ȃ��A���Ƃ��Ɠ��v�����}�j���A�����Ӑ}���ď�����Ă���̂ŁA�ǎ҂��߂������A�����̎�œ��v���������A���{����ۂ̃}�j���A���Ƃ��Đ�������邱�Ƃ���]���Ă���B
�@�u�g�D�������̂��߂̏]�ƈ��ӎ������v���̂�1986�N�ȗ����N6���`���N1����8�J���������āA(��)���{���Y���{���o�c�A�J�f�~�[�u�l�Ԕ\�͂Ƒg�D�J���v�R�[�X��ɂ��āA�M�҂ɂ���ČJ��Ԃ��J��Ԃ����E���{����Ă������̂ł���B1991�N�܂łɁA�ׂ̂Ŗ�50�ЁA��5,000�l�ׂĂ������ƂɂȂ�B
�@���̒����ł́A��ƊԂł̉��f�I�Ȍ����O���[�v�����A���̃����o�[��Ƃ̊Ԃœ����ɓ���̈ӎ��������s���A��ƊԁE�E��Ԃ̔�r�W�v���s���B�������ʂ̊�ƊԔ�r�ɂ���Ď��Ђ̕�������_��T��A���Ђ̎����m�b����Ȃ���A���Г��̎��ጤ�����s���Ƃ����v���Z�X���J��Ԃ����ƂŁA�����O���[�v�𒆐S�Ƃ��đg�D�̊������Ɋւ����蔭����}��v���O�����ƂȂ��Ă���B���́u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A�]�ƈ��̈ӎ��������s�Ȃ����Ƃ��_�@�Ƃ��Ė�蔭���v���Z�X���i��ł����̂ł���B
�@���̂����{���ň����̂́A���������v���Z�X�̑O���ɑ������鎿��[�����A������A���P�[�g�����̊��A�v����W�v�A���͂Ɏ���܂łł��邪�A�W�v�A���͂ɂ��ẮA���ɑ�2�`5�͂ň����Ă����̂ŁA���̏͂ł͒ʏ�̎Љ���̃v���Z�X�̋敪�Ō����ƁA��{�v�A�����[�E�W�{�v�A���n�������������Ƃɂ���B
�@����ł́A�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̎菇���A����ǂ��Đ������Ă������B���ۂ̒����菇�͐}6.1�̂悤�ȃt���[�`���[�g�ɂ܂Ƃ߂邱�Ƃ��ł���B���̃t���[�`���[�g�ɂ����āA����N(19XX�N)�ɍs��ꂽ�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ŁA���ۂɎg�p���ꂽ���������͖̏��Ɍf�ڂ��Ă���BA�`F�̎����������̂ǂ̒i�K�Ŏg�p���ꂽ���̂��́A�}6.1�̃t���[�`���[�g�̒��Ɏ����Ă���̂ŁA�Q�l�ɂ��Ăق����B�������A�������e�ɂ͔���J��O��ɂ��Ă�����̂��܂܂�Ă���A��Ж����A���J���Ċe���ʂɂ����f�̂����邨����̂�����̂ɂ��ẮA�ꕔ�A���O������A����s�\�Ȃ悤�ɓ��e��ς����肵�Ă���B
�}6.1�@�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̑O������(����[����)�̒����菇�Ǝg�p����
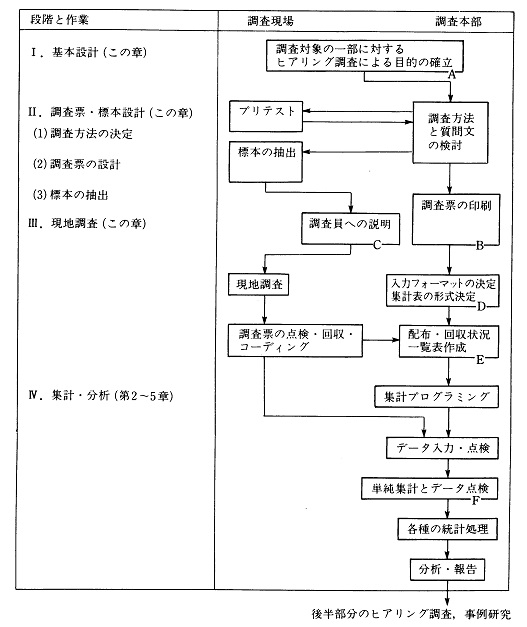
�@�܂���������悷��ۂɂ́A�����̖ړI�m�ɂ���K�v������B��̓I�ɁA�o���A��ʏ펯�A���邢�͗��_�Ɋ�Â��ĉ����𗧂Ă�ƁA�����ړI�͎���ɖ��m���A��̉����Ă���B
�@���̍ۂɒ��ӂ��K�v�Ȃ̂́A�����̉��������ꂼ�ꏭ���̒������ڂŊm���߂�����A�����̉����𑽐��̒������ڂŊm���߂���������̌����������A�܂����͂ɂ��[�݂��o��Ƃ������Ƃł���B���������āA�����ړI�ƂȂ鉼���́A�ł��邾���i���������悢�B�����̉������݂��ɂ�����Ƃ����W���^����ꂸ�ɕ������Ă���悤�ȏꍇ�́A�����𗧂Ă�Ƃ������ꂩ�炷��Ɠw�͕s���ł���B���f���͒P���ŁA�����łȂ���ΐ����͂������Ȃ����A���f���Ƃ͂����Ȃ��̂ł���B
�@�����̖ړI���m�����A���v�����̊�{�I�ȕ��j�𗧂Ă邽�߂ɂ́A�܂����O�ȃq�A�����O��������n�߂�̂��悢�B���O�ɂ��Ȃ�͂����肵���ړI��m���������Ă���悤�ȏꍇ�ł��A���ۂ̒����Ώۗ\��҂ɑ��ăq�A�����O�������s�����Ƃ́A�����[�̐v�����l����Ƌɂ߂ėL�v�ł���B�q�A�����O�����͖ʐڒ����̈��ł��邪�A��1�͑�4���ŏq�ׂ������[��p�����ʐڒ����@���A�����[��p���邱�ƂŁA(a)����̎d���A(b)�̎d���A�����i�ɒ�߁A���ꂵ�Ă��āA�w���I(directive)�ʐڒ����ƌĂ��̂ɑ��āA�s��^�Œ����҂̎��R�ɔC����Ă��邽�߂ɁA��w���I(non-directive)�ʐڒ����ƌĂ��B
�@�������A���ۓI�ɂ́A��w���I�ȃq�A�����O�����Ɏw���I�Ȗʐڒ�����g�ݍ��킹�čs�������������I�ł���B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A�͖�����A�ɂ���悤�ɁA�e�g�D����������_��e�����o�[�̖��ӎ���T���w���I�ȃq�A�����O�������s���Ă��邪�A���̑O�ɁA����ƕ������̌`�ŁA�u��b�����[�v���g���āA�w���I�Ȗʐڒ������K���s���Ă���B����́A��ɂ́A�q�A�����O�����̍ۂ̔w�i�I�m�����l������Ƃ������Ƃł��邪�A���̖ړI�ƂƂ��ɁA��Ƃɂ���ĈقȂ�u���t�v��u�T�O�v�m�ɔF�����A�q�A�����O�����̍ۂɁA�e�Ђ��Ƃ́u�����v���ł��邾���u�W����v�ɖ|�Ȃ����b���邱�Ƃ��o����悤�ɂȂ邽�߂ɕK�v�ȍ�ƂȂ̂ł���B����������A�̍�Ƃƃq�A�����O������ʂ��āA�͂��߂Đl�X���e��ƁA�e�g�D�̒��ŁA�������g���A�Ɠ��Ș_�����g���ē����Ă���Ƃ������Ƃ��A�����Ƃ��ĔF�������̂ł���B�܂��A���������v���Z�X���o�Ȃ���A�����̊�ƁA����ŋ��ʂ��Ďg�p���\�Ȏ��⒲���[����邱�Ƃ��ł��Ȃ��B��ʂ̎Љ���A���_�����Ɣ�r���Ă��A�o�c�g�D����������ő�̃|�C���g�́A��Ɗ����̊j�S�I�����ɋߕt���ߕt���قǁA��Ƃɂ���āu�����v�������g���Ă��āA���������̂��Ƃɓ����̐l�Ԃ��C�Â��Ă��Ȃ��Ƃ����_�ł���B
�@�����������Ƃ������āA���̒i�K�ŁA�����Ώۗ\��̎҂̈ꕔ�ɑ��āA���O�ȃq�A�����O�������s�����Ƃ��]�܂����B����[�����ɂ���Č����Ă݂�������������ꍇ�ɂ́A�q�A�����O�����ɂ���āA�����̑Ó�����(�������A�����ΏۂɂƂ��ĈӖ��̂�����̂��ǂ������܂߂�)������x�m���߂Ă����K�v������B
�@�����ɂ���ďo�Ă��铝�v�����́A���������q�A�����O�����ɂ��S�̐��x���グ����̂ɉ߂��Ȃ��A�Ƃ������x�ɍl���Ă��������悢�B
�@����ł́A�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ŁA�q�A�����O��������̓I�ɂǂ̂悤�ɍs����̂����܂Ƃ߂Ă������B�q�A�����O�������͖�����A�̊�b�����[�p���Ȃ���s����B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A�����̊J�n�ɓ����āA��N6���ɑ�1��̍��h���s����B�͖�����A�ɂ�����悤�ɁA��1�h�̑�1�ڕW�́A����̃O���[�v�����̓��c�̍ۂ̊�b�ƂȂ�L�[���[�h�A�R���Z�v�g�̔F�����ł��邾�����ꂵ�Ă������ƁA�������͔F���̈Ⴂ�m�ɂ��Ă������Ƃɂ���B�������e�r���厖�Ȃ킯�����A�����Ȃ��悭�Ȃ�̂ł͂Ȃ��A�e�X�̊�Ƃ̒��ł́A���̊�Ƃ̕������g���ĉ�b���s���Ă��邱�ƁA�����āA�u�����펯���悻�̏펯�v�Ƃ����Öق̑O�邢�͉������ԈႢ�ł��邱�Ƃ�������x�C�t�����邱�Ƃ���ł���B���ۂɂ͒����̃v���Z�X���i��ŁA����[�����̓��v�������o�Ă���܂ł́A�Ȃ��Ȃ��[���̏o���Ȃ����̂炵�����A���̍ŏ��̍��h�́A���̂��������ƂȂ�悤�ɍs����K�v������B
�@���h�́A��N3���Ԃɂ킽���āA�O���[�v�̃����o�[�S�����z�e���Ɋʋl�ɂ��āA�����ɂ�12���ԑO��A���ۂɂ͔�����ɂ���A�A���R�[���������Ă���[��Ɏ���܂ōs����̂ŁA����v���X8���Ԓ��x�̓q�A�����O���s����B���̃q�A�����O�ł́A�܂�1�l1���Ԓ��x��ڈ��ɂ��Ă�����āA��Ђ̊T�v�Љ�Ɖ�Ђ̓����Ɩ��_����Ă��炤�B�͈���I�ɔ��\����̂ł͂Ȃ��A���₪����l�͒N�ł��A���ł��A���̏�Ŏ��₪�o����悤�ɂ��Ă����B���̒i�K�ł́A��O�҂Ƃ��ē����Ă��錤���҂��A���悵�Ď��₵�Ă����K�v������̂Œ��ӂ�����B�����������������J��Ԃ��Ă݂�Ǝ��R�ɂ킩���Ă��邱�Ƃ����A�Ǝ���Ƃ̌��ɂ���Ă��A�g�����Ӗ��̈قȂ�p��A�T�O���K������̂ŁA���������_�����܂߂Ɏ��₷�邱�ƂŁA����ɋc�_�̎����������Ă�����̂ł���B���������o�������Ƃ��Ȃ��Ă��A�m�����ӂ�����Ȃ��ŁA�f�p�Ɏ����ςݏグ�Ă������Ƃ��̗v�ł���B
�@��Ђ̊T�v�Љ�͏���̗p���ɑ������`�ŗv�_�����Ƃ������ƂɂȂ��Ă��邪�A���炩���߁A�͖�����A�ɂ����鏊��̊�b�����[�ɋL�����Ă�����ŊT�v�Љ���s���̂ŁA���ʂƂ��Ă͏\���Ȃ��̂ƂȂ�B���₪������Ă���̂ŁA�ʏ���\����Ă���f�[�^��ǂނ̂Ƃ͈قȂ�A���̊�Ƃ̎����╵�͋C��m�邱�Ƃ��o����B��b�����[�ɂ��鍀�ڂ͗�N�̍��h�̍ۂɁA���������O���[�v�����Řb��ɂȂ��������A���邢�́A�����̊�b�����[�ɂ͋L�������Ȃ��������߂ɁA���̏�ō��Ȃǂ��g���Đ������s��ꂽ�悤�Ȃ��Ƃ�N�X�lj����Ȃ���`������Ă������̂ł���B����������A�ŏ��ɖ��炩�ɂ��Ă����Ȃ��������߂ɁA�c�_�̍����̌����ƂȂ������̂����I�ɂ܂Ƃ߂����̂Ƃ������Ƃ��ł���B
�@����������b�m������ɂ��āA��Ђ̓����Ɩ��_����Ђ̊������ɑ��鎩���̖��ӎ��𒆐S�ɂ��ĕ��Ă��炤�B����͔�w���I�ȃq�A�����O�����ł���̂ŁA����̗p���͗p���Ȃ����A�g�߂ȃG�s�\�[�h�������āA�������ɑ��鎩���̍l���A���ӎ����܂Ƃ߂Ă��炢�A�ꉞ���������ł͂Ȃ��A���ɏ����Ă��Ă��炤���Ƃɂ��Ă���B����́u�����v�Ƃ�����Ƃ��A�����̍l�����܂Ƃ߂邽�߂ɗL�p������ł���B
�@�͖�����A�̊�b�����[�̑g�D�}�́A����[�����̒����ΏۂƂȂ�g�D�P�ʂ�I�Ԃ��߂ɂ��p��������̂ŁA�����J�n�����ɓ��邱�̑�1�h�̒i�K�ŁA���߂Ɋe�����z�肵�Ă��钲���Ώۑg�D�P�ʂ�\�����Ă��炤���ƂɂȂ�B����́A�q�A�����O�����͈�ʘ_��b����Ă������ɂ͂Ȃ�Ȃ��̂ŁA��̓I�ɁA��Ƃ̂ǂ̕�����O���ɘb���Ă���̂��𖾂炩�ɂ��Ă����K�v�����邩��ł���B����ɂ����A���͍����̑��Ƃł͊�ƋK�͂����ɑ傫�����߂ɁA1�l�̐l�������ł���u��Ɓv�͎��ۂ̊�Ƃ̂����ꕔ�����ɂ����Ȃ��B��ōs���鎿��[�����́A���������u�����\�v�ȕ��������ɑΏۂ����肵�čs����B�������Ȃ���A���v�����̂����Ă���Ӗ��A�܂���Ԃm�Ɋm�肷�邱�Ƃ͏o���Ȃ�����ł���B���������āA�����̏����������̏�A�������Ă݂����Ǝv���Ă���g�D�P�ʂ��������ݒ�A�}�����Ă݂Ă��炢�A���̍ہA�ł���Αg�D�P�ʂ��Ƃ̑�܂��Ȑl�����L�����Ă��炢�A�u�����\�v�ȕ������m�F���Ă��炤�̂ł���B
�@��̓I�ɂ́A�l���K��50�l�ȏ�100�l�����̃z���C�g�J���[�̏W�c��g�D�P�ʂƂ��āA��܂��͕����I��ł��炤���ƂɂȂ�B�����ŁA�u�g�D�P�ʁv�Ƃ͑g�D�}��œ���̏�i�����E��������͐E��̏W���ŁA�Ⴆ�A�}6.2�̂悤�ȑg�D�}�ł͍א��ň͂܂�Ă���悤�Ȋe���x���̕����ɑ�������̂��Ƃ������Ƃ����炩���߂�����Ɛ������Ă����B
�}6.2�@�u�g�D�P�ʁv�̐ݒ�
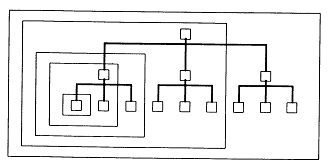
�@���̂悤�ɁA�P�Ɂu�E��v�Ƃ͂����ɁA�g�D�P�ʂ�ݒ肷��̂́A���͂̒i�K�ŁA�g�D�P�ʊԂ̔�r���͂��s���킯�����A�E��Ԕ�r�ł́A�e�E��̐l���K�͂ɊJ�������肷���邽�߂�(�ꍇ�ɂ���Ă�10�{���̍�������)�A���v�I�ɂ͔�r��������߂ł���B�������A�����̑S���قȂ�E�����̑g�D�P�ʂɉ������߂�悤�Ȃ��Ƃ͂��Ȃ��B���̏ꍇ�ɂ́A���Ƃ��l���K�͂��������Ă��A�g�D�P�ʂ͕ʗ��Ăɂ���B
�@���̑�1�h�̒i�K�ŁA�����X�P�W���[���̌��ʂ��𖾂炩�ɂ��Ă������Ƃ͏d�v�ł���B�O�N�x�P����`�ōs���ƁA�ǂ����������X�P�W���[���ɂȂ�̂��������A���̃X�P�W���[���ʼn������͂Ȃ����A���邢�́A���P���ׂ��_�͂Ȃ��������̒i�K�Ŋ��Ɋm�F���Ă����K�v������B���������ςɂ����A�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł͗�N��1�h�̌�A7����2��̃O���[�v�������s���A����Ă̌����E���c���s������ŁA�M�҂����������܂Ƃ߂�`�Ŏ��⒲���[�Ɏd�グ�A8��������9���͂��߂ɂ����āA1�T�Ԓ��x�������Ē����[�z�z�E������s����B�W�v��1�T�Ԃ�����ł���̂ŁA��r�I�����������ʂ��t�B�[�h�o�b�N���邱�Ƃ��o����B�t�B�[�h�o�b�N�����W�v�\�́A��̓I�ɂ͎��̂悤�Ȃ��̂ł���B
�@�����[�̐v�A���Ɏ��╶�̍쐬�́A�����Ƃ����Ӑ[���s����ׂ���Ƃ̈�ł���A�܂��A�����Ƃ��ʔ�����Ƃ̈�ł�����B�u�g�D�������̂��߂̏]�ƈ��ӎ������v�̏ꍇ�ɂ́A���̃v���Z�X�́A�e��Ƃ̒S���҂��玿�╶�̌�����`�Ŏn�߂���B�܂�A�����̑g�D������ɂ������āA���ꂾ���͒��ׂĂق������ƁA���ꂾ���͒m�肽���Ƃ������Ƃ��A�e���������Ŏ��╶�Ƃ��čl���Ă���悤�Ɂu�ۑ�v�Ƃ��ė^����̂ł���B
�@���̍�Ƃ͏��Ȃ��Ƃ�2�x�J��Ԃ����B1�x�ڂ͊e�����ł��邾���u�����̓��Łv���╶���l���Ă���Ƃ�����ƂŁA�ł��邾����̓I�ȁA���ۂ̊�Ɛl�������I�ɗ����ł���悤�Ȏ��╶���l���Ă��炤�B�������č��ꂽ���╶�́A�O���[�v�S�̂œ��c�����B���̍ۂ̓��c�̃|�C���g��
�@2�x�ڂ́A1�x�ڂɑ��̃����o�[���l���Ă������⍀�ڂ��܂߂��O���[�v�S�̂̑S����Ă̒�����A�u���l�̎���𓐂�Łv����������A���ꂾ���͎���Ă̒��ɓ���Ă����Ăق����Ƃ������╶��������x�������A1�x�ڂƓ�����Ƃ��J��Ԃ��̂ł���B
�@����������Ƃł̕\�������ړI�́A�u�W����v�ŏ����ꂽ���ʂ̎���[���쐬����Ƃ������Ƃł��邪�A���́A������d�v�ȖړI������B����́A�e�����o�[�̖��ӎ����@��N�����Ƃ������Ƃł���B���Ƀq�A�����O�����̍ۂɁA�e���̖��ӎ��ɂ��Ă������Ă���͂��ł͂��邪�A���̒i�K�ł́A���������ړI�ɖ��ӎ����\�������Ƃ������Ƃ����҂���͎̂��͂܂������ł���B�������A�e���ɁA���ꂾ���͒��ׂ����Ƃ������╶���l�������A�܂��I�������邱�Ƃɂ���āA���ݓI�ł����܂����������ӎ��������Ȍ`�ŕ\������Ă��邱�ƂɂȂ�B�������A�����������╶�͂��ꂼ�ꂪ��̉�����\�����Ă���ƍl������B�e�����o�[�ɂ͈ӎ�����Ă͂��Ȃ��Ă��A���Ȃ��Ƃ��u�����̑g�D�ł́A���̎���ɑ��Ă���ȉ��Ԃ��Ă��邾�낤�v���邢�́u�����̑g�D�̂��̎���ɑ��Ẳ��ʂ́A��i�A�����Ɍ�����Ƃ����Ɩ�肾�ƌ�����ɂ������Ȃ��v�Ƃ����������e�����Öق̂����ɂł��A�����Ă�����̂�����ł���B�����炱���A���Ђ��̎�����Ă݂����Ǝv�����͂��Ȃ̂ł���B
�@���������āA����������Ƃ́A��蔭���̃v���Z�X�Ƃ��Ă͔��ɏd�v�Ȃ��̂ƂȂ�B�����𗧂Ă�Ƃ������ꂩ�炵�Ă��A���̍�Ƃ͌����҂̂悤�ȑ�O�҂��Ɨ�������I�ɍs���ׂ��ł͂Ȃ��A�����܂ł��A�O���[�v�Q���҂���̎����I�Ȓ�Ă𑣂��A��������`�Ői�߂�ׂ��Ȃ̂ł���B
�@�����ŁA�����ł͎��⒲���[��v����ۂ̈�ʓI�Ȓ��ӎ����A����ш�ʓI�ȃe�N�j�b�N�A�m�E�n�E�ɂ��Ă܂Ƃ߂Ă������Ƃɂ��悤�B
�@���v�����ł̎���[�̎��╶�̍쐬�ɂ������ẮA�������ɁA���ԕ����Ə�ԕ����̓�̕���������A���҂̓������ӂ܂��Ď��╶�����K�v������B
�@����̓��e����������A���Ɏ���ɑ���̎d�������߂邱�ƂɂȂ�B�����ł܂��A����[�����̉v�I�ɏ������邽�߂ɕK�v�ȃR�[�f�B���O�̍�Ƃɂ��Ă܂Ƃ߂Ă������B�R�[�f�B���O(coding)�Ƃ́A���̍�Ƃ̑��̂ł���B
�@�R�[�f�B���O�ɂ́A�v���R�[�f�B���O�ƃA�t�^�[�R�[�f�B���O��2��ނ̕��@������B�v���R�[�f�B���O(pre-coding)�Ƃ͑����I���`���̂��Ƃł���B���̌`���ł́A����ɑ��A���炩���߉̑I�������p�ӂ���Ă���(���Ȃ킿�A���炩���߉̃J�e�S���[���A�L�������s���Ă���)�A�҂������̑I�����̒������I������Ǝ�����A�R�[�f�B���O���I�����邱�ƂɂȂ�̂ł���B
�@�A�t�^�[�R�[�f�B���O(after-coding)�Ƃ͎��R�`���̂��Ƃł���B���炩���߉̑I������p�ӂ��Ȃ��ŁA����ɑ�����҂Ɏv���t���܂܂Ɏ��R�ɉ��Ă��炢�A�I����ɁA�̃J�e�S���[��(categorization)�ɂ���ăR�[�f�B���O�̍�Ƃ��s�����ƂɂȂ�B
�@�R�[�f�B���O�ɂ�2��ނ̕��@������Ƃ����Ă��A���v�����ł͉\�Ȍ���v���R�[�f�B���O���s���A�����I���`�����̗p���ׂ��ł���B�Ȃ��Ȃ�A
�@���̎��R�`���̌��_�ƊW������̂����A�����I������̏ꍇ�ł��A�I�����̒��ɖ�����Ɂu���̑��v���܂߂�ׂ��ł͂Ȃ��B�u���̑��v�͌����l�Ɠ����Ӗ����������Ȃ����Ƃ������̂ł���B�u���̑��v����ꂸ�ɍςނ悤�ɁA�O��I�Ɏ��O�̃q�A�����O�������s���ׂ��ł���B�u���̑��v��I�����Ƃ��Ċ܂߂邱�Ƃ́A���O�̃q�A�����O�����̕s���s�������⒲���[�̒��ō������Ă���悤�Ȃ��̂ł���B
�@����ł����炩�̗��R�Ńq�A�����O�������\���ɍs�����A���╶�̉̑I���������炩���ߗ\�z�ł��Ȃ��悤�ȏꍇ�ɂ́A�v���e�X�g���s���Ă݂�Ƃ悢�B�v���e�X�g(pre-test)�Ƃ́A�{�����ɐ旧���A�����̒����Ώۂɑ��āA���╶�̌�����̕��z�Ɍ��������邽�߂ɍs�������ł���B���╶�̉̑I���������炩���ߗ\�z�ł��Ȃ��悤�ȏꍇ�́A�v���e�X�g�ł͎��R�`���ʼn��Ă��炢�A�o������ׂĕ��ނ��A�{�����̑I�������쐬����B��ɁA�A�t�^�[�R�[�f�B���O�܂莩�R�`���́A�v���e�X�g�Ŗ{�����ɂ�����v���R�[�f�B���O�̃J�e�S���[��ݒ肷�邽�߂ɗp������ƍl����ׂ��ł��낤�B
�@�v���R�[�f�B���O�Ŋ��ɑ����I���`���̑I������p�ӂ��Ă��܂��Ă���悤�ȏꍇ�ł��A�v���e�X�g�́A1�x�͍s���Ă����ׂ��ł���B�������A���������ꍇ�̃v���e�X�g�́A�{�ԓ��l�̕����ŋK�͂����������čs���Ƃ������̂łȂ��Ă��悢�B�ʐڒ����@��ʑO�L���@�̌`���Ƃ�Ȃ�����A�I�����u�āv�ɂ��Ă̗����Ȉӌ��悷��Ƃ����C�����ŁA���╶�A�I�����̐������s���Ă��悢�̂ł���B
�@�Ƃ���ŁA���R�`���́A�����Ƃ͕ʂ̖ړI�ŗp�����邱�Ƃ�����B�܂�A���ۂ̊�ƂȂǂł́A�҂̂����Ă���s���̃K�X�����̖ړI���߂ɁA���R�`���𑽗p�����A���P�[�g���g�p���邱�Ƃ��݂���B�������A�����̖{���̖ړI�͎����Ƃ��Ă̓��v�f�[�^�邱�Ƃł���A���̂悤�ȃK�X�����̖ړI���܂߂Ē������邱�Ƃ́A�{���̖ړI�Ȃ��\��������A�s���ׂ��ł͂Ȃ��B
�@�v���R�[�f�B���O�̑����I���`���̏ꍇ�ł��A�I�����̒�����Y�������I����ۂ̑I�����ɂ́A���̂悤�Ȏ�ނ�����B
�@��q����悤�ȃN���X�\���쐬����ۂ̗e�Ղ��A�N���X�\���̂̊Ȗ����Ɛ����͂��l����ƁA�ł��邾��1�̑������(SA)���]�܂����B����ɁA���␔��100���ڂɂ��Ȃ�悤�ȏꍇ�ɂ́A������œ�̎��⍀�ڊԂ̑��ւ��݂Ă����ƁA��5�͑�5��(3)�ł������悤�ɁA������ (100�~100-100)��2��4,950�� �̃N���X�\�ƌ����������ƂɂȂ�B����قǂ̖����ł����C���t���[���̑��ł͂����Ƃ����ԂɏW�v���Ă���邪�A���͂�������ė�������l�Ԃ̑��̔\�͂̕��Ɍ��E������Ƃ������Ƃł���B�����܂߂Ď��̒m�����A���̖��d�Ȏ��݂ɂ��܂����������l�Ԃ͂��Ȃ��B���������āA�������(SA)�̒��ł��A�ł������AYes-No�`���̂悤�ɁA��ґ���^�̎���ɂ��邱�Ƃ��]�܂����B�Ƃ����̂́A��5�͑�5���ł������悤�ɁA2�~2�N���X�\����ł���A�e�N���X�\����̑��W���ő�\�����A���W�������Ŕ�r���邱�Ƃ��\�ɂȂ邩��ł���B����Ȃ�A������ł����֊W�ׂ邱�Ƃ��o����B
�@��������(MA)�ł��A����̒��̊e�I�������`���I�ɁA���Yes-No�`���̎���Ƃ��Ĉ����ăN���X�\����邱�Ƃ͉\�ł���B
�@�I�����̃J�e�S���[�̐ݒ��̒��ӂƂ��ẮA
�@�ߋ��ɗD�ꂽ����������ꍇ�ɂ́A�ł���Ηގ��̕��ރJ�e�S���[���̗p���Ă����ƁA���̒������ʂƂ̔�r���\�ɂȂ�A�����̉̕蓙���l����ۂɎQ�l�ɂȂ�B
�@�Ō�ɋZ�p�I�Ȃ��Ƃł��邪�A�R�[�h�͂ǂ����Ă��������Ȃ��悤�Ȏ���Ȃ����萔����p���邱�ƁB���v�p�b�P�[�W(SAS��)�ƃR���s���[�^�̓s���ł͂��邪�A��X�̏������y�ɂȂ�A�Ⴆ��SAS�Ȃ�APROC�X�e�b�v�ł̐�����C�ɂ����ɍςށB�����āA�f�[�^�E�G���g���[�̍ۂ��A�e���E�L�[�����œ��͂��ł���̂ŁA�G���g���[�E�~�X�̗U����h���ƂƂ��ɁA���v���Ԃ��Z���čς݁A�O�������ꍇ�ł��f�[�^�E�G���g���[��p�̐ߖ�ɂȂ���̂ł���B
�@���⒲���[�ɂ͉҂̑���(���ʁA�N��A�E��A�E�ʂȂ�)��������K���݂��Ă����B����������{����(classification data)�́A���͂̊�ƂȂ���̂ŁA���̎���ɂ��Ă��A��{�����Ƃ̊W�͂��Ă������Ƃ��]�܂����B���̊�{���������͒����[�̖`���ɒu����邱�Ƃ����������̂ŁA��{�������ڂ̂��Ƃ��A�����A�t�F�[�X�E�V�[�g(face-sheet)���ڂƌĂԂ��A����͘a���p��B���݂ł́A�����ɒu�����Ƃ������B�p���I�ɒ������s���ꍇ�ɂ́A�����@��ɂ������������̕��ނ��m���A�m�肵�Ă������Ƃ��A�p���I�ȃf�[�^�̏W�ρA��r�̍ۂɊ�b�Ƃ��ĕK�v�ł���B
�@��{�����́A���̂���ɂȂ�ǂ�ǂ�ڂ������e�̎������邱�Ƃ��ł��邪�A�ڂ����Ȃ��Ă͂����Ȃ��Ƃ��A�ڂ�����Ώڂ����قǗǂ��Ƃ������Ƃ͂Ȃ��B�ނ���A���܂�ڂ������e�̌l�����ƁA�҂̑��Ɍx���S���ĂыN�������ƂɂȂ�A������A�L�����̒ቺ���������ƂɂȂ�B�펯�I�ɍl���Ă��A��{�����̍��ڂ������Ȃ�A�l�̓��肪�e�ՂɂȂ�A���������ێ��ł��Ȃ��Ȃ�B����܂ł̌o�����炷��ƁA�����E�����̕ʂ�w�������Ƃ͕��͏�̃����b�g�͂قƂ�ǂȂ��A�������Ă��������f�����b�g�̕����傫���B
�@�Ⴆ�A�����E�����̕ʂɂ��ẮA���̑���������܂łɕ��͂ɖ𗧂������Ƃ͂Ȃ����A���̎��⎩�̂ɕs���������l�����Ȃ肢��B����ɁA�����E�����̑��ɁA���ۂɂ͗����A���ʁA���̌�̍č��̃P�[�X�Ȃǂ�����A���܂�ɑI�������ו�����������B�u�z��҂̗L���v�����@�����邪�A����Ƃē����̍Ȃ�v�̑��݂��ǂ������ׂ����A�����̈Ӑ}�Ƃ��W���Ă���B���ǁA�{���ōl���Ă���悤�Ȓ����ł́A����������������邱�Ǝ��̂ɁA�ǂ�ȈӖ�������̂��킩��Ȃ��B
�@�܂��w���̏ꍇ�A�����Ƃ̓��蕔��́A�قƂ�Ǔ����I�Ȋw���������Ă���W�c�ɂȂ��Ă���̂ŁA��Ƃƕ������肷��A�w���͂قړ���ł��Ă��܂��̂����ʂł���B���̂��Ƃ����邽�߂ɁA�w���ɂ���ĉɍ��ق�������悤�ȃP�[�X�ł��A�ڂ�����������ƁA���ۂɂ͊�Ɗԍ��فA����ԍ��ق̔��f�ɂ����Ȃ��ꍇ���قƂ�ǂł���B�w���ɂ�镪�͂́A��ƊԔ�r�A����Ԕ�r�̍ۂɂ́A�����I�ȈӖ����قƂ�ǂ����Ȃ��Ƃ����Ă������낤�B
�@���̂��Ƃɂ��ẮA������2�͑�4��(3)�ł��G�ꂽ���A�͖�����B�̎��⒲���[�̂悤�ɁA���ꂾ������̍��ڐ��������Ȃ�ƁA�ϐ������݂��ɏd�����Ȃ��悤�ɔz�����Ȃ���A�e���⍀�ڂɑΉ������ϐ������l���邱�Ƃ͂����ւ�ȍ�ƂƂȂ�B�܂��ގ��̕ϐ����������Ȃ邽�߂ɁA��������ꂽ����(SAS�ł͉p������8�����ȓ�)�̕ϐ������������āA�����Ɍ��̎������肷�邱�Ƃ͎���̋Z�ƂȂ�B�����ŁA�ϐ����ɂ͎���̔ԍ������̂܂ܗp���A�ϐ��̈Ӗ����e�ɂ��Ă͕ϐ����x����p���邱�ƂŏW�v�\�̏�ŕ\�����邱�Ƃ̕������p�I�ł���B�ϐ����x���ɂ��ẮA�����̐������啝�Ɋɂ��Ȃ��Ă��邵�A�������g���邱�Ƃ������̂ŁA���Ȃ������ŏ��ʂ̑傫�ȕϐ����x������邱�Ƃ��ł���B�܂�A�ϐ����ŕϐ��̈Ӗ����e��\��������͂����Ɗm���Ŏ��p�I�ł���B
�@�������A�ϐ����Ɏ���ԍ������̂܂ܗp����Ƃ����Ă��A��2�͑�4���ł��q�ׂ��悤�ɁA�ϐ����̍ŏ���1���͐����ł͂����Ȃ��Ƃ����\�t�g��̐�����̂ŁA����̑啪�ނ̓��[�}�����ɂ��Ă����ƕ֗��ł���B���[�}������I�AV�AX�AL�Ȃǂ̃A���t�@�x�b�g�ō\�������̂ŁA�ϐ����̓��ɂ����Ă��Ă��A���̂܂ܕϐ����Ƃ��ėp���č����x���Ȃ��B�Ⴆ�A�u����II��1�v�u����V��5�v�Ȃǂ͂��ꂼ��uII1�v�uV5�v�Ǝ���ԍ������̂܂ܕϐ����ɂł���̂ł���B
�@�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A���Ƀq�A�����O�����̒i�K�Őݒ肵�Ă������g�D�P�ʂ�ΏۂƂ��āA���̐��Ј��̑S�����������邱�Ƃ������Ƃ��Ă���B�S�������ɂ��闝�R�́A���̂悤�Ȃ��̂ł���B
�@�ȏ�̂悤�Ȓ����Ώۂ̐ݒ�Ӑ}������A�m�F������ŁA�����̎d���E�菇�ɂ��ẮA�͖�����C�u���n�����̎���v�Ƃ����������������Ƃɂ��Ď��O�Ɍ����Ő������A�m�F���Ă����B���́u���n�����̎���v�́A�e�Ђɂ����钲���菇������������̂ŁA�e�Ђɂ����钲���́A����2�i�K�ɕ����čs�����ƂɂȂ�B
�@�����̐i�ߕ��Ƃ��ẮA�܂���1�i�K�Ƃ��āA�e�ВP�ʂɁu�z�z�E��������[�v�ɋL�����Ă��������ŁA������A���̒i�K�Œ����Ώۂ��ŏI�I�Ɋm�肷��B�Ȃ��A���̒����Ώۂ̐ݒ�͐T�d�ɐi�߂�K�v������B�����̎������肷����̂�����ł���B���������āA�O�ɂ͔O�����āA��Ƒ��ɋ^��_��������A���ł��A�C�y�ɖ₢���킹���o����悤�ɔz�����Ă������Ƃ��d�v�ł���B��Ƒ��ɂƂ��Ă͏����ȋ^��_�ł��A��2�i�K�̎��⒲���[�̔z�z�O�ɉ������Ă����Ȃ��ƁA���Ԃ��̂��Ȃ����ƂɂȂ�\�������������ɂ��Ă�����̂ł���B�Ⴆ�A�����̏ꍇ���͂Ȃ��̂����A�g�D�P�ʂ������́u�E��敪�v�i�z�z�E��������[���Q�Ɓj�ɂ܂�����Ȃ��悤�ɐݒ肳��Ă��邱�Ƃ��m�F���邱�Ƃ��K�v�ł���B�܂�A�u1. �����E�X�^�b�t�v�u2. �Z�p�E�����v�u3. �����E�J���v�u4. �̔��E�c�Ɓv�̂ǂꂩ�Ɏ��܂邱�Ƃ��m�F����̂ł���B
�@�����āA���̂Ƃ��ɁA�o���I�ɂ͒����[�̉���������S�̂�400�`500��������A�W�{�덷��}���邱�Ƃ��o���A���v������A���Ȃ茩�h���̂��錋�ʂ�������Ƃ������ƁA���������āA���̒����ł̖��͉�����������A�ނ��������̕��ł���A��W�{�덷��}���邽�߂ɁA������̖ڕW��90�����x�Ƃ��Ă��������Ƃ������Ƃm�ɑł��o���A�g�D�P�ʂ�ݒ肷��ۂɂ́A�ł��邾��������������ێ������܂܂ŁA�K�v�ȉ��������������悤�Ȕz�����������Ă������Ƃ�Y��Ȃ��悤�ɁB������͎���[�����̎��ƐM���������肷��̂ł���B
�@�ȏ�̂��Ƃ𒍈ӂ�����ŁA�����ΏۂƂȂ�g�D�P�ʂ��������ݒ肵�Ă��炢�A�u�z�z�E��������[�v�̃R�s�[��������A�m�F���āA���̒i�K�ł܂߂ɂ�����Ƃ����Ǘ������Ă������Ƃ��d�v�ł���B
�@��2�i�K�́A��1�i�K�Ŋ��ɐݒ肵�Ă���g�D�P�ʂɂ��āA������\�����鐳�Ј��S����ΏۂƂ�������[�����ł���B�z�z�������܂ł̊��Ԃ�1�T�ԂƂ����̂͒Z���Ɗ������邩������Ȃ����A�o���I�ɂ́A����̃s�[�N�͔z�z����ƒ�o�����O���2��ŁA���̊Ԃ̊��Ԃ́A���ꂪ���Ȃ蒷���ɐݒ肵�Ă����Ă��A�قƂ�lj�����Ȃ����̂ł���B�܂����ۂɂ́A��o��������A����ł���܂�1�T�Ԓ��x�̗]�T���������Ă��邪�A���̊��Ԃɉ���ł��镔�����o���I�ɂ͂���قǑ������̂ł͂Ȃ��B1�T�Ԃłł��邾�������W�߂�̂���Ԍ����I�Ŋy�ȕ��@���Ƃ������Ƃ𗝉��E�[�����Ă��炤�����Ȃ��B
�@�܂����⒲���[�̃R�[�h�E�{�b�N�X�̋L���̎d���͏\���ɐ������Ă����K�v������B���⒲���[��z�z����ۂɂ́A���Ƃł킩��Ȃ��Ȃ�Ȃ��悤�ɁA���ۂɔz�z����������z�z�E��������[�́u�z�z�����v�́u���ہv�̗��ɋL�����Ă��炤�B���⒲���[������������⒲���[�͑g�D�P�ʕʂɕ��ނ��A�g�D�P�ʂ��ƂɎ��⒲���[��2�y�[�W�ڂ̃R�[�h�E�{�b�N�X�̌�2���ɁA��A�ԍ����L�����Ă��炤�B�����āA���ۂɉ���������⒲���[�̕�����z�z�E��������[�́u��������v���ɋL�����Ă��炢�A������𐳊m�ɔc������̂ł���B
�@���ۂɉ����ł���̂́A�����̒��ߐ�̂ق�1�T�Ԍ�ł���B��ނ����Ȃ��ꍇ�₻�̌����ł������͂ł��邾�����������A���ۂɏW�v��Ƃ��n�܂��Ă��܂��A���炾��ƒlj�����킯�ɂ͂����Ȃ��̂ŁA����ł���͖������Ă������ƁB
�@�܂��͖�����B�ɂ�����悤�ɁA���⒲���[�̕\���ɂ́A�W�v���͎҂𖾂炩�ɂ��A�����[���[�̂܂ܗ��p����邱�Ƃ̂Ȃ����Ƃ�ۏ�����ŁA���̏W�v���͎҂̘A����m�ɂ��Ă���̂ŁA���̑Ή����ӂ�Ȃ����ƁB����́A��N�A��������1���₢���킹�����邩�ǂ����ł͂��邪�A�W�v���͎҂��m�F�ł���Ƃ������S�����A�����̎������コ����̂ł���B
�@�����[�̐v���܂����ƁA�R�[�f�B���O�����Ȃ��Ă͂Ȃ�Ȃ��悤�Ȃ͂߂Ɋׂ邱�ƂɂȂ�̂ł��邪�A�u�g�D�������̂��߂̏]�ƈ��ӎ������v�ł́A�����[�̐v�̒i�K�Ńv���R�[�f�B���O����O�ɍs���A�f�[�^�����ׂĐ����f�[�^�ɂ��Ă���̂ŁA���͂͒����[�����Ȃ��璼�ڍs�����Ƃ��o����B�������A�͖�����D�ɂ���悤�ɁA���̓t�H�[�}�b�g�����́A�^��̗]�n�̂Ȃ��悤�Ȑ��m�ɒ�`���Ă����ׂ��ł���B���̓t�H�[�}�b�g�́A�����[�̉�����I��O��(���ۂɂ͉�����Ԃ�1�T�Ԃ����Ȃ��̂ŁA���⒲���[�̊��������)�A�쐬���Ă������Ƃ��]�܂����B�܂��ASAS�ŏW�v����ꍇ�ɂ́A�����l�̓s���I�h "." �œ��͂���悤�Ɋm�F���Ă����B�f�[�^�E�G���g���[���Ǝ҂ɊO������ꍇ�ɂ́A�f�[�^�͎��C�e�[�v�A������MT�ɓ�����Ĕ[������邱�Ƃ������̂ŁA���C�e�[�v�ɏ������ތ`���ɂ��ẮA�Ǝ҂Ƃ����k���āA���炩���ߌ��߂Ă����K�v������B
�@�����[�̉�����I���ƁA�f�[�^�E�G���g���[�ƕ��s���āA�͖�����E�̂悤�ȁu�z�z�E����ꗗ�\�v���쐬����B�����ŏd�v�Ȃ̂͑g�D�P�ʂ��Ƃ̉�����𐳊m�Ɋm�肵�Ă������Ƃł���B���̐����́A�P���W�v���s���āA�f�[�^�ƃv���O�����̃`�F�b�N���s���ۂɎQ�Ƃ��ׂ���b�I�����Ȃ̂ŁA�K���W�v��Ƃ̎n�܂�O�ɍ쐬�A�m�肵�Ă������ƁB
�@�ȏオ���ۂ̒����菇�ł���B�����܂ł���A���Ƃ͎��ۂ̏W�v��Ƃɓ��邾���ł���A�{������2���ň����Ă���P���W�v���珇�ɕ��͂�i�߂Ă����悢�̂ł���B
6.1�@��b�����[ �@�w��Ўl�G��x�w��Џ��x�Ȃnj��ɂ���Ă���ŐV�ł̎������g���āA�����̋����̂�����1�Ђɂ��āA�͖�����A�̊�b�����[�̉�ЊT�v�����[�ɋL�����A�ł��邾�����������Ă݂悤�B���ꂩ�牽���킩�邩�B�܂��A���̂悤�Ȍ��ɂ���Ă��鎑���ł͂킩��Ȃ��������̉��l�ɂ��čl���Ă݂�B
6.2�@�v���e�X�g �@�팱�҂ɂȂ�������ŁA�͖�����B�̎��⒲���[�Ɏ��ۂɉ��Ă݂�B���̍ہA���̓_�ɒ��ӂ��Ȃ������B
�@��1�h�̑�1�ڕW�́A����̃O���[�v�����̓��c�̍ۂ̊�b�ƂȂ�L�[���[�h�A�R���Z�v�g�̔F�����ł��邾�����ꂵ�Ă������ƁA�������͔F���̈Ⴂ�m�ɂ��Ă�������(���e�r)�ɂ���܂��B
| �@�@�@6��14�� | 14:00�`18:00�@ | �O���[�v���c |
| 15�� | 9:00�`12:00�@ | �O���[�v���c |
| 13:00�`17:30�@ | �O���[�v���c | |
| 19:00�` | �����̒��Ԕ��\�̏������ | |
| 16�� | 9:00�`11:30�@ | ���Ԕ��\(���ӎ��̂܂Ƃ߁A�ł���Ό����e�[�}) |
����ꂽ���ԓ��ɎQ���ґ��݂̗�����[�߂邽�߂ɁA�����͉������B
�@�O�N�x���Q�l�ɂ����
| �@�@�@7�� | 2�� | �@����Ă̌����E���c |
| 16�� | �@����Ă̌����E���c | |
| 8�� | 27�� | �@���⒲���[���� |
| 28�� | �@�����[�z�z | |
| 9�� | 3�� | �@�����[�_���E����(�����[�L�ڂ̉��������2��) |
| 9�� | 24�� | �@�W�v�\�� |
| 10�� | 8�� | �@�W�v�\�����Ƃɂ�����ƊԔ�r |
| 10�� | 18�`20�� | �@���h: �W�v�\�����Ƃɂ����E��Ԕ�r |
�@�{�Ђ̒��̐l���K��50�l�ȏ�100�l�����̃z���C�g�J���[�̑g�D�P�ʂ���܂��͕����I�сA���̑g�D�P�ʂ̐��Ј��̑S�������������Ƃ��܂��B�����ŁA�u�g�D�P�ʁv�Ƃ͑g�D�}��œ���̏�i�����E��������͐E��̏W���ł��B�Ⴆ�A���̐}�ŁA�א��ň͂܂�Ă���悤�Ȋe���x���̕����ł��B

�s�S�������ɂ��闝�R�t
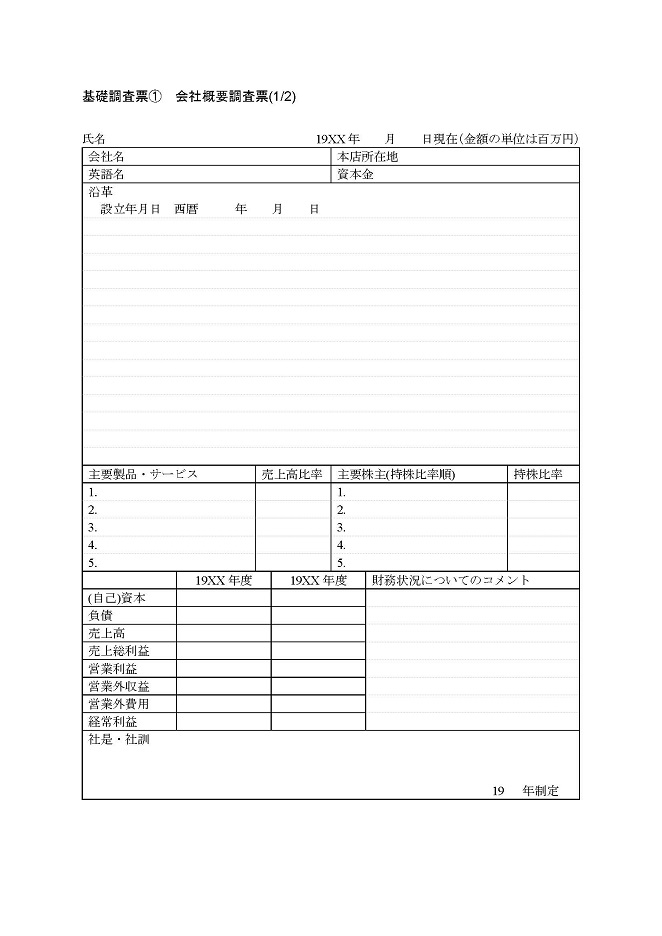
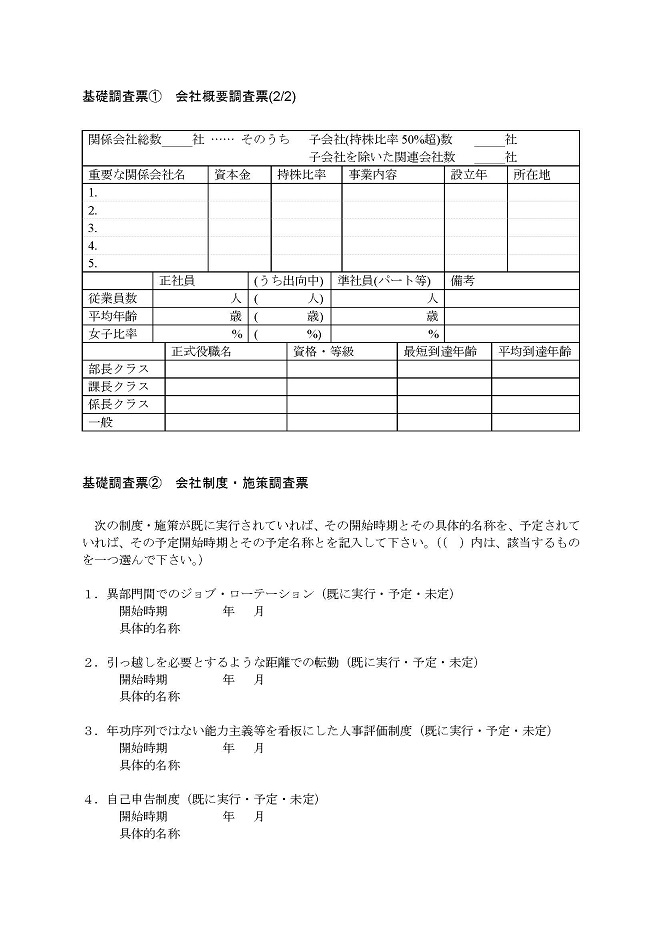

�O���[�v�̊F�����
�@����̃O���[�v�����ł̓��c����ɁA���⒲���[�̌��Ă��쐬���܂����B���������������B
�@�����ł�8��27��(�Ηj��)�ɁA�������{���Y���{���o�c�A�J�f�~�[�܂Ŏ��Q���A���n���������ł��B���̍ۂɁA�����Œ����̎d���ɂ��Ă��������������ł���܂����A���O�ɁA����Y�t���Ă���uC. ���n�����̎���v�Ƃ���������������n�ǂ���������A�����̎d���͂�����������������̂Ǝv���܂��B���s���̓_�́A���̍ۂɂ܂Ƃ߂Ă����₢�������Ă����\�ł����A�^��_��������܂�����A�����@��ɂ��d�b����������K���ł��B
�@�Ȃ�����̓����́uC. ���n�����̎���v�̒��Ɂu���n�����E�W�v�X�P�W���[���v������܂��̂ł��Q�Ƃ��������B
19XX�N8��





�@���́u���n�����̎���v�́A�e�Ђɂ����钲���菇������������̂ł��B�e�Ђɂ����钲���́A����2�i�K�ɕ����čs���܂��B
�@�����̐i�ߕ��Ƃ��ẮA�܂���1�i�K�Ƃ��āA�e�ВP�ʂɁu�z�z�E��������[�v�ɉ̏�A8��27��(�Ηj��)���A���{���Y���{���o�c�A�J�f�~�[�܂ł��������������B
�@����ł́A�����A�u2. ��1�i�K�����̎菇�v�ɂ����������n�ǂ̏�A�Y�t���Ă���u�z�z�E��������[�v�̑��g���ɋL�����Ȃ���A��1�i�K������i�߂Ă��������B
�@�Ȃ��^��_��������܂�����A���ł��A���C�y�ɂ��₢���킹���������B�^��_�͑�2�i�K�̎��⒲���[�̔z�z�O�ɉ������Ă����Ȃ��ƁA���Ԃ��̂��Ȃ����ƂɂȂ�\��������܂��̂ŁA�ǂ�ȏ����ȋ^��_�ł��A���C�y�ɂ��₢���킹���������B�m�A����nTEL 000-000-0000 �����L�v
�@���ɁA�ǂ����ΏۂƂ������̂��ɂ��ẮA�����܂��ɂ��������������Ă���܂����A����[������ڑO�ɂ��āA�����Ώۂm�ɒ�`���A���̐l���I�ȑ傫�����m�肵�Ă����K�v������܂��̂ŁA���ꂩ��q�ׂ�悤�ȍl�����ɉ����āA�g�D�P�ʂ����ۂɐݒ肵�Ă��������B
�@��2�i�K�����̎���[�����ł͐��Ј��̐l���K��30�`50�l���x�̃z���C�g�E�J���[�́u�g�D�P�ʁv���������I�сA���́u�g�D�P�ʁv�ɂ��ẮA���̐��Ј��̑S�������������Ƃ��܂��B�����ŁA�u�g�D�P�ʁv�Ƃ͑g�D�}��œ���̏�i�����E��������͐E��̏W���ł��B�Ⴆ�A���̂悤�ȑg�D�}�ł́A�א��ň͂܂�Ă���悤�Ȋe���x���̕������g�D�P�ʂ̌��Ƃ��čl�����܂��B

���̌��ƂȂ郌�x���̒�����A�ǂ̃��x���ɑg�D�P�ʂ�ݒ肷�邩�́A
�@�o���I�ɂ͒����[�̉���������S�̂�400�`500��������A���v������A���Ȃ茩�h���̂��錋�ʂ������܂��B���������āA���͉�����������A�ނ��������̕��ɂȂ�܂��B����܂ł̌o������A������̖ڕW��90���ȏ�Ƃ��Ă����������̂ł��B���̖ڕW������͖��m�Ȋ�ɂ͒v���܂��A�g�D�P�ʂ�ݒ肷��ۂɂ́A�ł��邾��������������ێ������܂܂ŁA�K�v�ȉ��������������悤�ɔz�����Ă��������B������͎���[�����̎��ƐM���������肵�܂��B
�@�ȏ�̂��Ƃɗ��ӂ��ꂽ��ŁA�����ΏۂƂȂ�g�D�P�ʂ����̊1�A2�ł������ݒ肵����ŁA�Y�t�́u�z�z�E��������[�v�̑��g���ɋL�����āA8��27��(�Ηj��)���A���̃R�s�[����{���Y���{���o�c�A�J�f�~�[�܂ł��������������B
�@��2�i�K�́A��1�i�K�Ŋ��ɐݒ肵�Ă���g�D�P�ʂɂ��āA������\�����鐳�Ј��S����ΏۂƂ�������[�����ł��B8��28��(���j��)�Ɉ�Ăɔz�z���Ă��������A���⒲���[�ɋL�ڂ���Ă����o�����A9��2��(���j��)�܂łɉ�����Ă��������B�z�z�������܂ł̊��Ԃ�1�T�ԂƂ����̂͒Z���Ɗ������邩������܂��A�o���I�ɂ́A����̃s�[�N�͔z�z����ƒ�o�����O���2��ŁA���̊Ԃ̊��Ԃ͂قƂ�lj�����Ȃ����̂̂悤�ł��B�܂��A���ۂɂ͒�o��������A����ł���܂�1�T�Ԓ��x�̗]�T����������\��ł����A���̊��Ԃɉ���ł��镔�����o���I�ɂ͂���قǑ������̂ł͂���܂���B�����͂ЂƂo������߂āA1�T�Ԃłł��邾�������W�߂�̂���Ԍ����I�Ŋy�ȕ��@���Ǝv���܂��B��2�i�K�̎菇�͈ȉ��̒ʂ�ł��B
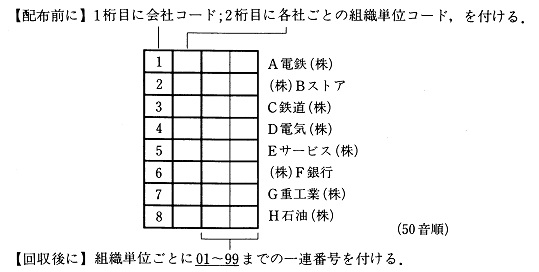
�@���̍ہA���ۂɔz�z����������z�z�E��������[�́u�z�z�����v�́u���ہv�̗��ɋL�����Ă��������B
�@���̍ہA�z�z�E��������[�́A����������⒲���[�̔������ɁA���̓s�x�A�t�@�b�N�X�ʼn��L�̓�����w���ɑ����Ă��������B���ɑ��钲���[�́u�����ʒm�v�����˂Ă���܂��B
�@����Ȍ�̓������́A�W�v��Ƃ��n�܂��Ă��܂��܂��̂ŁA�W�v�ɗp���邱�Ƃ��ł��܂���B�Ԃɍ��킹�邽�߂ɁA���������Ȃ���A�t�@�b�N�X�Ōo�c�A�J�f�~�[�܂ő����Ă��������Ă����܂��܂���B
����������⒲���[�̑��t��F ��150 �����s�a�J��a�J3-1-1 (��)���{���Y���{���o�c�A�J�f�~�[ �������� �� FAX 00-0000-0000 �z�z�E��������[�̑��t��F ��153 �����s�ڍ�����3-8-1 ������w���{�w���Љ�Ȋw�� �����L�v�@ FAX 00-0000-0000










�@CMS(Conversational Monitor System)��IBM�̃��C���t���[���p�ɊJ�����ꂽ��b�^��pOS�ł���BOS (Operating System)�Ƃ́A��2�͑�2���ł��q�ׂ��悤�ɁA�ȒP�Ɍ����A�O���L�����u����o�͑��u�Ƃ������n�[�h�E�F�A�𑀍삷��\�t�g�E�F�A�̂��Ƃł���B
�@���ۂɂ�1��̃��C���t���[�����z�X�g�E�R���s���[�^�ɂ��āA����ɂ�������̒[�����Ԃ炳���đ���������Ă���B�܂�A1��̃z�X�g�E�R���s���[�^���̗��p�҂ɂ���ċ��p���Ă���̂ŁA�������Z�������u�A��L�����u���͂��ߊO���L�����u����o�͑��u�Ƃ����������̔z���A�Ǘ��𗘗p�ҊԂŒ������Ȃ��Ă͂Ȃ�Ȃ��͂��ł���B�Ƃ��낪�ACMS�ł́A�[���ŗ��p�҂����O�I������ƁA���̗��p�Ґ�p�̉��z�v�Z�@(Virtual Machine)���N�����邱�ƂɂȂ�B�����I�ȃR���s���[�^�E�V�X�e�����ӎ������ɁA�e���̗��p�������R�ɐݒ�ł��邵�A���z�v�Z�@�ɂ͉��z���o�͑��u���ڑ�����Ă��邱�ƂɂȂ�B�e���p�҂͑��̗��p�҂�C���t���[���̑S�̓I�ȊǗ����C�ɂ��邱�ƂȂ��A��������������p�̃p�[�\�i���E�R���s���[�^���g�p���Ă��邩�̂悤�ɁA�[���𗘗p���邱�Ƃ��ł���̂ł���B����CMS�̎g�p���@�A���p�̌��ߎ������o����A�������ǂ̂悤�ȃz�X�g�E�R���s���[�^�̃n�[�h�E�F�A�A�@����g�p���Ă���̂���m�炸�Ƃ��A���C���t���[���̃z�X�g�E�R���s���[�^���g�p���邱�Ƃ��ł���B
�@�R�}���h���͂̕\�L���@�ɂ��ẮA��2�͑�2��(4)�Ő����������̂Ɗ�{�I�ɓ����ł��邪�A�قȂ�̂́A�����I�ɁA�R�}���h���͂̍ۂɂ́A���^�[���E�L�[�̑���ɁA(���s)�L�[�������Ƃ������Ƃł���B���^�[���E�L�[�ɂ�����(���s)�L�[�ł͂Ȃ��̂Œ��ӂ��Ăق����B(���s)�L�[��������ʂ��o�Ă��ĕ��G�Ȃ̂ŁA���̏͂ł́A���̓s�x�L�[�̎�ނ�\�����邱�Ƃɂ��悤�B�[���̎�ނɂ���ẮA(���s)�L�[��(ENTER)�L�[�A(���s)�L�[��(���)�L�[�̂��Ƃ�����̂ŁA���̏ꍇ�ɂ͓ǂݑւ��邱�ƁB
�@CMS�ɂ�����t�@�C��(file)�܂��̓f�[�^�E�Z�b�g(data set)�Ƃ́A�����I�ɂ̓z�X�g�E�R���s���[�^�̌Œ�f�B�X�N�Ɋi�[���ꂽ�v���O������f�[�^�̏W���̂��Ƃł���B�t�@�C���͘_���I�ɂ͗��p�҂��ƂɐU�蕪����ꂽ���z�́u�~�j�E�f�B�X�N�v�ɕۊǂ���Ă���B
�@�p���`�E�J�[�h���g���ē��͂��s���Ă�������ɂ́A�v���O������f�[�^�̓p���`�E�J�[�h�Ƀp���`����A�p���`�ɂ���ĊJ����ꂽ�������w�I�ɃJ�[�h�E���[�_�[�ƌĂ��ǎ�@�B�œǂݎ���ăR���s���[�^�ɓ��͂��Ă����B�p���`�E�J�[�h�P����80���̐����A�A���t�@�x�b�g�������̓J�^�J�i���p���`���邱�Ƃ��ł����B�����ł����Ă���1�������������ނׂ��ꏊ�̓p���`�E�J�[�h�̏ꍇ�ɂ̓J����(column)�ƌĂꂽ���A����1����������1�J�����́A���̗ʂƂ��Ă�1�o�C�g(byte)�ɑ������Ă���B�܂�p���`�E�J�[�h1����80�J��������Ȃ�A80�o�C�g�̏�����͂��邱�Ƃ��ł������ƂɂȂ�B
�@���݂ł́A�p���`�E�J�[�h�͂قƂ�ǎg�p���ꂸ�A�[��������o�͂��s���邪�A�[���̉�ʂ̏��1�s�����̃p���`�E�J�[�h1���ɑ������A����1�s�ɏ����ꂽ�f�[�^�����R�[�h�ƌĂԁB�t�@�C���́A���m�ɂ͂��̃��R�[�h�̏W���ł���B�p���`�E�J�[�h�̎���ɂ́A�R���s���[�^�Ɏ��s���������v���O������f�[�^���p���`�E�J�[�h�Ƀp���`���A���̃J�[�h�̑�(������J�[�h�E�f�b�N�ƌĂ�)�������Ȃ���ΗփS���ł܂Ƃ߁A������������t�@�C�����O�E�P�[�X�ɓ���ĕۊǂ�����A�����������肵�Ă����B�J�[�h�E���[�_�[�ɃJ�[�h��ǂݎ�点��Ƃ��ɂ��A���̑��P�ʂŃJ�[�h�E���[�_�[�ɂ����Ă����B���̑��������u�t�@�C���v�������̂ł���B���Ȃ݂ɁA��ʓI�Ȓ[���̉�ʂ̍��[����E�[�܂�1�s�����ς��ɕ�������͂���Ɣ��p������80��(�܂�80�o�C�g)����悤�ɂȂ��Ă���̂́A���̃p���`�E�J�[�h�̖��c�ł���B
�@�����I�ɗp���̑傫���̋K�i�����ꂳ��Ă����p���`�E�J�[�h�Ƃ͈���āA�[������̓��͂ł͉��s����܂ł�1�s�ł���A�ʂɊe�s��80���ɌŒ肵����A(80���ł͂Ȃ��Ƃ�)�e�s�̒����𑵂����肵�Ȃ���Ȃ�Ȃ����R�͂Ȃ��B���������āA�F�X�Ȍ`���̃t�@�C�������݂����邱�ƂɂȂ�킯�����ACMS�ł̓t�@�C���̑����Ƃ��āA����4��\�����Ă���邱�ƂɂȂ��Ă���(��4���Ō�q����FILELIST�R�}���h�Q��)�B
�@�W���I�ȃt�@�C���̌`���́A
�@�e���R�[�h�͍s�ԍ���t���邱�Ƃ��t���Ȃ����Ƃ��ł���B�����ł����Ă���s�ԍ��́A��ŕҏW�̂��ƂɐG���ۂɏo�Ă���ҏW��ʏ�A���[�ɕ\�������u�s�ԍ��v�̂��Ƃł͂Ȃ��A�e���R�[�h�ŗL�̍s�ԍ��ł���B������J�[�h����̖��c�ŁA���Ă̓J�[�h�̑��𗎂����肵�ď��Ԃ����`�����`���ɂȂ����Ƃ��ł��A���̍s�ԍ��̂������ŋ~��ꂽ���̂ł���B���������āA���݂ł͕t���Ă��t���Ȃ��Ă��A�قƂ�LjӖ��͂Ȃ��B�������ɂȂ�̂́A�s�ԍ�������ۂɂ́A�e���R�[�h�̍Ō㕔8�o�C�g(73�J�����ځ`80�J������)���g���čs�ԍ����������܂��Ƃ������Ƃł���B���̂��Ƃ͒��ӂ�v����B�����s�ԍ��Ȃ��̃t�@�C�����s�ԍ��t���̃t�@�C���ɕς����Ƃ��ɂ́A���R�[�h�Ō㕔��8�o�C�g���̃f�[�^���������Ă��܂�����ł���B�f�[�^�̃t�@�C���͌�ŃR�[�f�B���O�E�~�X��p���`�E�~�X�̒������s�����Ƃ������̂ŁA���̍ۂɂ悭����킩��Ȃ��܂܂ɁA�I�v�V�������w�肵�Ă��܂����肵�āA�s�ԍ�������ď�������ł��܂������ꂪ�Ȃ��Ƃ͂����Ȃ��B���������āA�Ⴆ�A�Œ蒷�A80�o�C�g�̃J�[�h�E�C���[�W�̃t�@�C�����쐬����ۂɂ́A���ʂ̎���Ȃ�����́A�������̗p�S�̂��߂Ɋe�s��1�`72�J�����݂̂��g���A�Ō㕔��8�J�����͎g�p���Ȃ��悤�ɂ���BSAS�v���O��������̓f�[�^�͍s�ԍ��t���ł��s�ԍ��Ȃ��ł��悢���ƂɂȂ��Ă���̂ŁA�s�ԍ��Ȃ��Ŏg���Ă��A���̕�������ł���B
�@�t�@�C�����ʎq(fileid�Ƃ������\�����)�̓f�[�^�E�Z�b�g��(data set name: dsname)�Ƃ��Ă�邪�ASAS�ł̓t�@�C�����f�[�^�E�Z�b�g�ƌĂԂ̂ŁASAS�̒��ł̓f�[�^�E�Z�b�g���ƌĂԂ̂��ʗ�ł���B�t�@�C�����ʎq�̗�Ƃ��ẮA
�@�@�@NEWFILE SAS A1
�̂悤�ɂȂ�A�t�@�C�����ʎq�͋�(�u�����N)���͂���
�@�킩��₷�������ƁA1. �t�@�C���E�l�[��(fn)�� 2. �t�@�C���E�^�C�v(ft)�̑g�Ńt�@�C���̖��O��\���Ă���B����ΐl�̐����Ɠ����ŁA2. �t�@�C���E�^�C�v(ft)�����A�����A1. �t�@�C���E�l�[��(fn)�����ɑ������Ă���BSAS�̃v���O�����́uSAS�Ƃ̈���v�Ƃ������ƂŁuSAS���v�𖼏��A�t�@�C���E�^�C�v�Ƃ���SAS��p���邱�ƂɂȂ��Ă���BSAS�͂���ȊO�̃t�@�C���E�^�C�v���������t�@�C����SAS�v���O�����̃t�@�C���Ƃ��āu�F�m�v�����A�t���Ȃ��̂Œ��ӂ�����B����ɑ��āA3. �t�@�C���E���[�h(fm)�͏Z���ɑ������A�ǂ��̒n��(�~�j�E�f�B�X�N)�Ƀt�@�C�����u�Z��ł���̂��v�������Ă���B���ɒf��Ȃ���A�~�j�E�f�B�X�NA�A�܂莩�����Z��ł���uA�n��v�ɏZ��ł���ƍl����ɂȂ��Ă���B
�@CMS�ł́A���o�͑��u�͊���l�Ƃ��Ē[���݂̂��w�肳��Ă���B�t�ɂ����ƁA�[�������Œʏ�̓��o�͎͂�����Ă���킯�ł���B�������A�f�[�^�����ɑ傫���Ƃ���A���̃R���s���[�^����f�[�^��������Ă���Ƃ��A���邢�̓n�[�h�E�R�s�[�Ƃ��Ă�����Ǝ��̏�Ɉ�����Ďc�������Ƃ��ł��A�[�������ʼn䖝����Ƃ����킯�ł͂Ȃ��B�[���ȊO�̓��o�͑��u�A�Ⴆ�A�ǎ摕�u�A���E���u�A���C�e�[�v���u�A������u�Ƃ��������u�Ƃ̓��o�͂́A��{�I�ɂ͎��̂悤�ɍl���čs�����ƂɂȂ��Ă���B
�@���̂����A1�Ŏ��C�f�B�X�N���CMS�t�@�C����_���I�ɓ��o�͑��u(���z���o�͑��u)�ƌ����Ă���ŁA����l�Œ[���ƂȂ��Ă�����o�͑��u�̐ݒ������CMS�t�@�C���ɕύX����ɂ́A�f�[�^��`��(data definition name: ddname)��p���Ē�`���s���B���̈�A�̑���ɂ��Ă܂Ƃ߂Ă������B
�@fileid�Ŏ����ꂽ���C�f�B�X�N���CMS�t�@�C������o�͑��u�ƌ����Ă�ۂɂ́A
�@�@�@FIledef ddname DISK fileid(���s)
�Ⴆ�A���̂悤�ɓ��͂���悢�B
�@�@�@FI 18 DISK OUT91 DATA(���s)
�����ŁA�Ⴉ����킩��悤��ddname�́u���z���o�͑��u���v�Ƃ͂Ȃ��Ă��邪�A���ۂɂ͓��o�͑��u�ԍ��ł悭�A�M�҂͗�ɂ���悤�� "18" �� "IN" �Ȃǂ��悭�g���B�������ԍ��ł悢�Ƃ͂����Ă��A11�`15�͎g���Ȃ����Ƃ�����B���l�ɁASAS���g�p����ۂɂ́A����ddname�͎g�p�ł��Ȃ��̂ŁA���ӂ�����B
�@�@�@LIBRARY, SASDUMP, SASLIB, SORTWKxx, SORTLIB, SYSIN, $SYSLIB, SYSOUT, WORK
�����Ŏw�肵��ddname�́A2�ʼn��z�v�Z�@�̓��o�͂�CMS�t�@�C���ɑ��čs���ۂɁA���z���o�͑��u���Ƃ��ē��Y���u�ԍ����w�肳��邱�ƂɂȂ�B
�@�����������z���o�͑��u���̎w����������A����l�̒[���ɖ߂��ɂ�
�@�@�@FIledef ddname CLEAR(���s)
�Ⴆ�A���̂悤�ɓ��͂���悢�B
�@�@�@FI 18 CLEAR(���s)
���̂悤�Ɋe���u�����ƂɎw�����������̂ł͖ʓ|�ȏꍇ�ɂ́A�S�Ă̐ݒ���������A����l�̒[���ɐݒ��߂����Ƃ��\�ł���B���̂Ƃ��ɂ́A���C���h�E�J�[�h"*"���w�肵�āA
�@�@�@FIledef * CLEAR(���s)
�Ɠ��͂���悢�B���C���h�E�J�[�h�܂萯�� "*" �́u�Y�����鍀�ڂ̂��ׂāv���Ӗ����Ă���B
�@�����ł́A�[�����炻�̓s�xCMS�ɃR�}���h����͂��邱�Ƃ��l���Ă��邪�A���ۂ̃P�[�X�ł́ASAS�̃v���O�������ŁuX CMS�R�}���h�v�̌`���g����̂ŁASAS�v���O�������Ŏ��̂悤�Ɏw�肵�������������Ȃ��ł��ށB
�@�@�@X FIledef �c�c�G
�@���̂悤�Ƀf�[�^��`�����`���邱�Ƃɂ��A�}7.1�̂悤�ɉ��z���o�͑��u��CMS�t�@�C���̑Ή������邱�Ƃ��ł���B
�}7.1�@���z�v�Z�@�Ɖ��z���o�͑��u
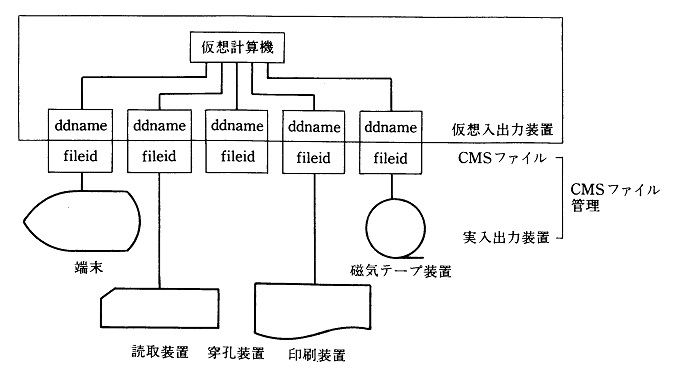
�@���̐}�̒��̉��z�ǎ摕�u�A���z���E���u�A���z������u�͂܂Ƃ߂ĉ��z���j�b�g�E���R�[�h���u�Ƃ����A�����u�Ƃ̊Ԃł̓��o�͂�CMS�t�@�C���̊Ǘ��̌`�ōs����B�������A���݂ł͎��ۂ̃R���s���[�^�E�V�X�e�����ǎ摕�u�A���E���u�̎����u�������Ȃ����Ƃ������A���̏ꍇ�ɂ́A���ꂼ�ꂪ���͗pCMS�t�@�C���A�o�͗pCMS�t�@�C���̈Ӗ����������Ȃ��B�܂����C�e�[�v���u�͐ڑ��䐔�����Ȃ��A���������C�e�[�v���u�ɂ́A�e���p�҂��g�p���鎥�C�e�[�v���펞�������Ă���킯�ł͂Ȃ��̂ŁA���C�e�[�v���u���g�p����ۂɂ́A���C�e�[�v���u�����z�v�Z�@�̓��o�͋@��Ƃ��Đڑ�����葱�������ʂɕK�v�ɂȂ�(���C�e�[�v���u�̎g�p�ɂ��ẮA��7�����Q�Ƃ̂���)�B
�@�ȏ�ŁA�����Ƃ���{�I�ȕ����̉���͏I�����̂ŁA���Ƃ͎��ۂɃz�X�g�E�R���s���[�^��������Ȃ���b��i�߂Ă������B����ł́A�Ƃɂ����[���@�̑O�ɍ����āA�z�X�g�E�R���s���[�^�Ɛڑ����Ă݂悤�B���̂��Ƃ����O�I������Ƃ����B�����̃��[�U�[���ƃp�X���[�h���������Ă���A���O�I���̎d���͂������ĊȒP�ł���B���̂悤�Ȏ菇�ł���Ă݂�ƁA�����Ƀz�X�g�E�R���s���[�^�Ƃ̉�b���\�ɂȂ�B
�@�������A3�ɂ��ẮA���[�U�[���̌�ł́A(���s)�L�[�͉������ɁA�p�X���[�h����͂�����ŁA(���s)�L�[�������B���[�U�[������͂���ƁA���̃L�[�ɐG��Ȃ��Ă������I�ɉ��s���A�p�X���[�h�s�ɃJ�[�\���������Ă���͂��Ȃ̂ŁA��ʂ��悭���邱�ƁB�����A���[�U�[������͂��Ă��A�p�X���[�h�s�ɃJ�[�\�����ړ����Ȃ��ꍇ�ɂ́A(���s)�L�[���������ƂɂȂ邪�A�[���ŁA���͂𑣂� "===>" �̕\���̌��ɓ��͂���ꍇ�ɂ́A���̒����1�J�����ɂ͓��͂ł��Ȃ����ƂɂȂ��Ă���̂ŁA�Ⴆ�A
�@�@�@===> TAKAHASI
�Ƃ����悤�ɁA�K��1�����A�J�[�\���E�L�[(�X�y�[�X�E�L�[�ł͂Ȃ�)�ł����ē��͂��邱�ƁB�ȏ�̎葱���������I������ƁA
�@�@�@LOGON ���[�U�[��
�@�@�@LOGON AT hh:mm:ss JST day mm/dd/yy
�@�@�@VM/SP REL 5 11/06/90 01:15
�ƕ\�������B����Ń��O�I�����ς�ŁATSS�������J�n����A�[���̓z�X�g�E�R���s���[�^�ł��郁�C���t���[���ɐڑ����ꂽ�I�����C���̏�Ԃɂ���B���̏�ԂɂȂ�ƁA�����[���̃L�[�{�[�h���g���āA�z�X�g�E�R���s���[�^�ɃR�}���h�𑗂邱�Ƃ��ł���B�v���O������f�[�^����͂��āA�z�X�g�E�R���s���[�^�Ɏd��(job)�������邱�Ƃ��ł���̂ł���B�z�X�g�E�R���s���[�^�ւ̗p���ς�A�[�����z�X�g�E�R���s���[�^���������Ă����B���̂��Ƃ����O�I�t����Ƃ����A���̂悤�ɂ���B
�@�܂����C���t���[���̏��S�҂ɑ����ʓI�ȃA�h�o�C�X����n�߂悤�B�[���̃f�B�X�v���C��ʂɐԐF�̕\�����o����A�z�X�g�E�R���s���[�^����́u�x���v�ł���B���������x������������̂͂������ĊȒP�ł���B(���)�L�[�܂���(RESET)�L�[�������悢�B�������A����ł͉�����̉����ɂ͂Ȃ��Ă��Ȃ��B
�@�x�����o���̂Ȃ�A�������邱�Ƃ��������Ă��d�����Ȃ��B�܂��C�𗎂����āA�Ȃ��x�����o���ꂽ�̂����l���Ă݂�K�v������B�����͕K�����p�҂̑��ɂ���B�����̏ꍇ�́u�^�C�v�E�~�X�v�������ł���B�������A���̃^�C�v�E�~�X�͍L���Ӗ��ł̃^�C�v�E�~�X�ŁA�[���𑀍삵�Ă��铖�l���A�u�^�ʖڂɊԈႦ�đ���v���Ă���ꍇ�A�܂�A�u�m�M�������ă~�X�v���Ă���ꍇ�ł��A���ꂪ�R���s���[�^�ɂƂ��āu�Ӗ��s���v�Ȃ�A�R���s���[�^�̑��ł̓^�C�v�E�~�X�Ƃ��Č`���I�ɔ��f����̂ł���B���������āA�Ȃ��x�����o���̂����m�F����K�v������B�قƂ�ǂ͖{���̂悤�ȃe�L�X�g��}�j���A���̓ǂ݊ԈႢ�A��ǂ������ł���̂ŁA������x���O�ɓǂݒ����āA�m�F���Ăق����B
�@����Ƃ�����B�z�X�g�E�R���s���[�^�͗��p�҂Ɖ�b���������Ă���B�������R���s���[�^�������o���Ęb���킯�ł͂Ȃ��̂ŁA�R���s���[�^������̌Ăт����́A���b�Z�[�W�Ƃ��Ē[���̃f�B�X�v���C��ʂ�ʂ��čs����B�Ƃ��낪�A���S�҂͂قƂ�lj�ʂ�ǂ܂Ȃ��B����ł͘b���������Ȃ��B�z�X�g�E�R���s���[�^����̃��b�Z�[�W�́A��ʂ̋��ɂ܂����o����邱�Ƃ������̂ŁA�R���s���[�^�Ɖ�b���邽�߂ɂ́A��ʂ̋��X�܂ŋC��z���Ă��K�v������B���肪�@�B������Ƃ����āA���p�҂͈���I�ɃR���s���[�^�ɖ��߂��邱�Ƃ�����l�����ɁA�R���s���[�^�̈ӌ���A�h�o�C�X�A���b�Z�[�W��������Ǝ~�߂Ă�銰�e�����K�v�ł���B�����F���R���s���[�^�̗��ꂾ������A�l�̎����ӌ��A�����ɂ�����݂����A��������I�ɃK�~�K�~�ƈ�ѐ��̂Ȃ����߂����A�v���ʂ�ɂȂ�Ȃ��Ɩ\�͂܂ŐU�邤�悤�ȃ��c(���܂Ɍ������邪��ɂ�߂Ăق���)�̌������Ƃ͕����Ȃ��͂��ł���B�R���s���[�^�����������ꍇ�ɂ͌������Ƃ��Ȃ��B���܂Ɍ��_�����邱�Ƃ͂����Ă��A�R���s���[�^�ƗǍD�ȁu�F�l�v�W��z���グ�Ăق������̂ł���B
�@�����ŁA�p�\�R���Ƃ͂�����Ə���̈Ⴄ�z�X�g�E�R���s���[�^����̃��b�Z�[�W�̓ǂݕ��̏����A��{���̊�{��\7.1�ɂ܂Ƃ߂Ă����̂ŁA�Œ���̉�b�����݂Ăق����B���O�I�����ăz�X�g�E�R���s���[�^�Ɛڑ�����ƁA��ʉE�����Ɏ��̂悤�ȃX�e�[�^�X(���V�X�e���̏��)���\�������B���ꂼ�ꂪ���p�҂ɑ��郁�b�Z�[�W�ƂȂ��Ă���̂ŁA�o���Ă����ƌv�Z�@�́u�l���Ă��邱�Ɓv���킩��B���̕\�̂����ŏ��̃P�[�X�A���Ȃ킿�������ɕ\�����Ȃ��A�E�����ɁuRUNNING�v�������\������Ă���ꍇ�́A�ʏ�̃X�e�[�^�X�ŁA����ɏ������s���Ă���Ƃ����\���ł���B���̃X�e�[�^�X�\���ɂȂ��Ă���ꍇ�ɂ́A����Ȃ�ɑΏ�����K�v������̂ŁA�\���Q�l�ɂ��Ăق����B
�\7.1�@��ʉE�����ɕ\�������X�e�[�^�X�ƑΏ����@
| �X�e�[�^�X | �Ώ����@�Ɓs�Ӗ��t | ||
|---|---|---|---|
| RUNNING | �������ɕ\���Ȃ� | �s���͑҂�: �ʏ�̕\���t | |
| �������ɢX ����X SYSTEM� | �s�z�X�g��ƒ��t | ���̏I���҂� | |
| �������ɐԂ��uXX�@�c�c �v | �s�둀��Ȃ̂Ŏ�����t | (���)�L�[�ʼn��� | |
| VM READ | (���s)�L�[�ŢRUNNING��\�� | �s�ʏ�̕\���t | |
| (���s)�L�[�ŢCMS��\�� | �s�R�}���h�̓��͑҂��t | ||
| (���s)�L�[�Ţ?��\�� | �s���s�v���O�����̃f�[�^���́t | ||
| CP READ | ���O�I���O: Logon(���s) | ||
| CMS�g�p��: B(���s) | ����ŕω��Ȃ���� I CMS(���s) | ||
| NOT ACCEPTED | �s�z�X�g��ƒ��t | ���b�҂��ăR�}���h�ē��� | |
| MORE... | �s1����Ɏ���ʕ\���t | ��~����ɂ�(���s)�L�[ �����\���ɂ�(CLEAR)�L�[ | |
| HOLDING | �s����ʕ\����ێ��t | ���̉����ɂ�(CLEAR)�L�[ | |
�@CMS�t�@�C���̊Ǘ��́A�����I��FILELIST�R�}���h�ɂ���ČĂяo���ꂽ�t�@�C���̈ꗗ�\�̉�ʂ��g���čs����B
�@���̂ǂ���̕��@�ł��AFILELIST�R�}���h�̎g�p���J�n���A�t�@�C���̈ꗗ�\��\�����邱�Ƃ��ł���B
| �@�@�@FILEList(���s) | ������ | �����ۗ̕L����t�@�C��(������fm=A)�̑S����\���B |
| �@�@�@FILEList * SAS(���s) | ������ | �uft=SAS�̃t�@�C���݂̂�\���v(���C���h�E�J�[�h�u*�v���g������) |
�Ⴆ�A�O�҂̕��@�ŁAFILELIST�R�}���h�ɂ���āA�����̃~�j�E�f�B�X�N�`�̑S�Ẵt�@�C����\��������ƁA�}7.2�̂悤�Ƀt�@�C���̈ꗗ�\����ʏ�ɕ\�������B
�}7.2�@FILELIST�R�}���h�ɂ��t�@�C���̈ꗗ�\(���߂ă��O�I�������Ƃ��̏��)
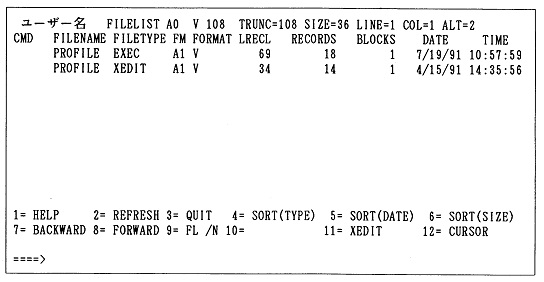
�@���̉�ʂ͂܂��t�@�C���������ō쐬�������Ƃ��Ȃ��g���n�߂̍ŏ��̏�Ԃ����������̂ł���B���̉�ʂ�����킩��悤�ɁA���̏�ԂŊ��ɁA�e���p�҂̃t�@�C���Ƃ��� PROFILE EXEC �� PROFILE XEDIT �̓�̃t�@�C�����K�������Ă���B���̓�̃t�@�C���́A���O�I���Ɠ����Ɏ����I�Ɏ��s����鏉���ݒ�t�@�C���Ȃ̂ŁA������Ȃ����ƁB�������̃t�@�C��������ƁA���� PROFILE EXEC �t�@�C���̕�������ƁA��{�I�Ȋ��ݒ肪�o�����A�ʏ�̎g�p�͕s�\�ɂȂ�̂Œ��ӂ��K�v�ł���B
�@���̐}�̂悤��FILELIST��ʂ̏�ԂŁA�L�[�{�[�h���PF�L�[���g����CMS�t�@�C���̊Ǘ����s�����Ƃ��ł���BFILELIST��ʂ�PF�L�[�̐ݒ肳�ꂽ�@�\�͉�ʂ̉����ɕ\�����ꂽ�ʂ�ŁA�����̋@�\�͔�r�I�悭�g�p����邽�߂�PF�L�[�ɐݒ肳��Ă���B
| �@�@PF1 | ��HELP | �R�}���h�A�@�\�ɂ��Ă̐�����\������B |
| �@�@PF2 | ��REFRESH | �]���ȕ\���������āAFILELIST��ʂ����t���b�V������B |
| �@�@PF3 | ��QUIT | FILELIST�R�}���h���I�����A�V�X�e���E���[�h�ɖ߂�B |
| �@�@PF4 | ��SORT(TYPE) | �t�@�C���E�^�C�v(FILETYPE)�ŕ��ނ��ĕ��ג������t�@�C���̈ꗗ�\��\������B |
| �@�@PF5 | ��SORT(DATE) | �쐬�N����(DATE)�ɂ��������ĕ��ג������t�@�C���̈ꗗ�\��\������B |
| �@�@PF6 | ��SORT(SIZE) | �t�@�C���̑傫�����ɕ��ג������t�@�C���̈ꗗ�\��\������B |
| �@�@PF7 | ��BACKWARD�@ | �O�̉�ʂɖ߂�B |
| �@�@PF8 | ��FORWARD | ���̉�ʂɐi�ށB |
| �@�@PF9 | ��FL /N | �J�[�\���s�̃t�@�C���Ɠ����t�@�C���E�l�[��(FILENAME)�̃t�@�C���̈ꗗ�\��\������B |
| �@�@PF10 | �� | |
| �@�@PF11 | ��XEDIT | �J�[�\���s�̃t�@�C����XEDIT�ŕҏW����B |
| �@�@PF12 | ��CURSOR | �J�[�\�����R�}���h�s�Ɉړ�������B |
�@���̂�����ԏd�v�Ȃ̂́AFILELIST�R�}���h���I��������PF�L�[�ŁA(PF3)�L�[(��QUIT)������ł���B���̃L�[�������ƁA
�@�@�@READY; T=n.nn/n.nn hh:mm:ss
�ƕ\������ACPU�g�p���ԂƃV�X�e���E���[�h(CMS�R�}���h���g������)�ɖ߂��������Ƃ��������B���̑��̋@�\�Ǝg�p���@�ɂ��Ă�(2)�ŐG���B
�@�����z�X�g�E�R���s���[�^���g���Ă��鑼�̗��p�҂ɑ��M����ꍇ�́A1��[ ]���̃m�[�h���͏ȗ����Ă����܂�Ȃ��B�m�[�h���͗Ⴆ�� "JPNUTKOM" �Ƃ���ƁA������w���{�w��2����6�K�̋@�펺�ɂ���IBM���C���t���[�����Ӗ����邱�ƂɂȂ�B���͂����bitnet�ƌĂ��l�b�g���[�N���̃m�[�h���ŁA���E���ǂ��ł��A����bitnet�ɉ������Ă���z�X�g�E�R���s���[�^�̃m�[�h�����w�肷��A���̃z�X�g�E�R���s���[�^�̗��p�҂ɑ��āA�t�@�C���𑗂邱�Ƃ��o����B�t�ɁA���h�Ƀ��[�U�[���ƃm�[�h����Ⴆ��
�@�@�@TAKAHASI AT JPNUTKOM
�ƍ��荞��ł����A���E����bitnet���p�҂���t�@�C������M���邱�Ƃ��o����B
�@���̗��p�҂���]������Ă����t�@�C������M���邽�߂ɂ́AFILELIST�R�}���h�Ɠ����x����RDRLIST�R�}���h���g���čs���BFILELIST�R�}���h���g�p���Ă���ꍇ�ɂ́AFILELIST��ʂ���U�I�����A�V�X�e���E���[�h�ɖ߂�����ŁARDRLIST�R�}���h���g�p����B
�@�z�X�g�E�R���s���[�^��CMS�t�@�C����[���ƂȂ��Ă���p�[�\�i���E�R���s���[�^��MS-DOS�t�@�C���ɃR�s�[���邱�Ƃ��o����B���̋t���\�ł���B���̍�Ƃ́A�z�X�g�E�R���s���[�^�ƒ[���ƂȂ��Ă���p�[�\�i���E�R���s���[�^�Ƃ̊Ԃł̃t�@�C���]���ƌĂ�Ă���B
�@�z�X�g�E�R���s���[�^�Ƀ��O�I��������́A��̃L�[����
�@�@�@(�O��)�{(�I��)
�Ɖ����ACMS�̃V�X�e���E���[�h��MS-DOS�̃V�X�e���E���[�h�Ƃ��X�C�b�`��on/off�̂悤�ɐ�ւ��B�z�X�g�E�R���s���[�^�ƒ[���ɂȂ��Ă���p�[�\�i���E�R���s���[�^�̊ԂŃt�@�C���]��������ɂ́A�z�X�g�E�R���s���[�^�Ƀ��O�I��������ŁAMS-DOS�̃V�X�e���E���[�h�ɐ�ւ��A�[�����̃\�t�g�E�F�A���g���čs���B���ܒ[�����̃f�B�X�N�E�h���C�uA�̃t���b�s�B�E�f�B�X�N�̂���MS-DOS�t�@�C����CMS�t�@�C��fn ft�ɓ]��(���m�ɂ̓R�s�[)����Ƃ��A�y�т��̋t�̃P�[�X�ł́AMS-DOS�̃V�X�e���E���[�h�ŁA���̂悤�ɓ��͂���悢�B
�@�s�[�����z�X�g�t
�@�@�@C:> SEND A:MS-DOS�t�@�C���� fn ft [(JISCII CRLF(���s)
�@�s�[�����z�X�g�t
�@�@�@C:> RECEIVE A:MS-DOS�t�@�C���� fn ft [(JISCII CRLF(���s)
�����ŁA"JISCII" �́AASCII�R�[�h��EBCDIC�R�[�h�ɕϊ����APC�����R�[�h��IBM�����R�[�h�ɕϊ�����Ƃ����Ӗ��A"CRLF" �́A�t�@�C���̒��̕���(CRLF)�R�[�h�����̂܂ܓ]������Ƃ����Ӗ��̃p�����[�^�ł���B
�@SAS�̃v���O������f�[�^�́A��2���ł�SAS��PROGRAM EDITOR�E�B���h�E�ō쐬���邱�Ƃɂ��Ă���B�������ACMS�̃G�f�B�^�[�ł���XEDIT�ɂ���č쐬���邱�Ƃ��ł���B�{���ł�XEDIT���g��Ȃ��Ă��ςނ悤�ɂ��Ă��邪�A�v���O������f�[�^���ڐA�A�]������l�́A���̐߂�(3)�̕����͕K�v�ɂȂ�̂ŁA�Œ�����������͓ǂ�ł������ƁB
�@�V����CMS�t�@�C������鎞�́A���̂悤�Ȏ菇�ɂ��������čs���B
�@������CMS�t�@�C����ҏW���鎞�ɂ́A
�}7.3�@XEDIT�̕ҏW���
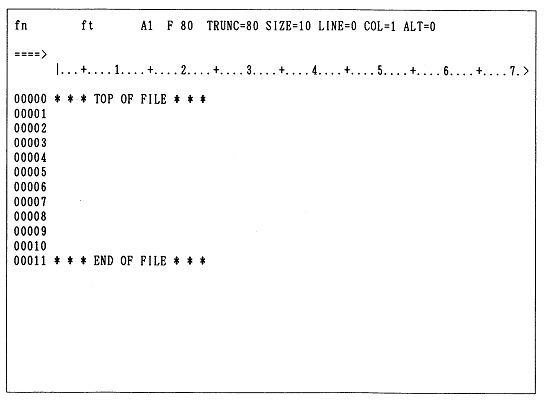
�@SAS�ł̓v���O�����E�t�@�C���͌Œ蒷�łȂ��Ǝt���Ȃ����A������v���O�������ڐA�A�]�������ꍇ�Ȃǂɂ́A�Ƃ��ǂ��ϒ��̃t�@�C���ƂȂ��Ă��܂��Ă��邱�Ƃ�����B���������ꍇ�ɂ́A�ϒ��̃t�@�C�����Œ蒷�̃t�@�C���ɕς��Ȃ��Ă͂����Ȃ��킯�����A���̂Ƃ��́A�V�K�̃t�@�C�����쐬���Ă���(�����I�ɌŒ蒷�̃t�@�C���ƂȂ��Ă���)�A���̃t�@�C���ɉϒ��̃t�@�C����ǂݍ��ނ��ƂŁA���e�Ƃ��Ă͑S�����ꂾ���A�`���������Œ蒷�ɕς�����t�@�C�����쐬���邱�Ƃ��o����B�܂�A���m�ɂ����A�ϒ��̃t�@�C�����Œ蒷�̃t�@�C���ɃR�s�[���邱�Ƃ��o����̂ł���B��̓I�Ȏ菇�́A
�@�_�E���T�C�W���O�̐i�s���钆�ł��A���C���t���[�����g�p����ő�̗��R�́A��ʂ̃f�[�^����舵���K�v������Ƃ������Ƃł��낤�B�����ŁA���̏͂̏I��ɁA��ʂ̃f�[�^�̃f�[�^�E�G���g���[���O�������ꍇ���l���A���C�e�[�v���u�̎�舵���ɂ��Đ������悤�B
�@���C�e�[�v(MT: Magnetic Tape)�Ɏ��̂悤�Ȍ`���ŏ�����Ă���t�@�C���������̃��[�U�[���̃f�B�X�N���CMS�t�@�C���Ƃ��ēǂݍ���(���m�ɂ̓R�s�[����)�P�[�X�������B
�@���̓ǂݍ��ݎ菇�̂����A1��2�̏������������A3�̎��C�e�[�v��̃t�@�C������̕����ɂ́A����Ɏ��̂悤��TAPE�R�}���h���g���āA���C�e�[�v���u���CMS�t�@�C���̑�����s�����Ƃ��ł���B
| �@�@�@TAPE REW | ������ | �e�[�v�����[�h�J�n�_�܂Ŋ����߂��B |
| �@�@�@TAPE RUN | ������ | �e�[�v�������߂��A�����[�h����B |
| �@�@�@TAPE SCAN fn ft | ������ | �������ăt�@�C�����ʎq�����X�g���A�t�@�C��fn ft�̒��O�ɒ�~�B |
| �@�@�@TAPE SKIP fn ft | ������ | �������ăt�@�C�����ʎq�����X�g���A�t�@�C��fn ft�̒���ɒ�~�B |
| �@�@�@TAPE LOAD fn ft | ������ | �e�[�v�E�t�@�C��fn ft���f�B�X�N�ɓǂݍ��ށB |
| �@�@�@TAPE DUMP fn ft (TAP1 DEN 6250 | ������ | �f�B�X�N�E�t�@�C��fn ft���e�[�v�Ƀ_���v����(�������ޖ��x��6250BPI)�B |
�I�v�V�����Ƃ��āASCAN, SKIP, LOAD, DUMP�����t�@�C���̃��X�g������������Ƃ��ɂ� "(PRint"�A �[���ɕ\���������Ƃ��ɂ� "(Term" ���w�肷�邱�Ƃ��o����B
�@��������TAPE�R�}���h�̓T�^�I�Ȏg�p��́A��w�̃z�X�g�E�R���s���[�^���g�p����ۂɔN�x�̕ς���(�܂胆�[�U�[���̕ύX�E�X�V����)�ɁA�����̃��[�U�[���̃f�B�X�N�ɕۊǂ���Ă���CMS�t�@�C�������C�e�[�v�ɑޔ��E�ۑ�����ۂ̎g�p��ŁA3�̕�����
�@�@�@TAPE REW(���s)
�@�@�@TAPE DUMP * * A (PR TAP1 DEN 6250(���s)
�@�@�@TAPE RUN(���s)
�Ƃ���ƁA�����̃��[�U�[���ɕۊǂ���Ă���S�Ă�CMS�t�@�C����6250BPI�Ŏ��C�e�[�v�ɃR�s�[���A�R�s�[�����t�@�C���̎��ʎq�̃��X�g���v�����^�Ɉ�������邱�Ƃ��o����B���̎��C�e�[�v���g���āA���[�U�[�����X�V���ꂽ��ŁA��͂�3�̕�����
�@�@�@TAPE LOAD * *(���s)
�Ƃ���ƁA���C�e�[�v��̑S�t�@�C�����f�B�X�N�ɓǂݍ��ނ��Ƃ��o����B
7.1�@�t�@�C���̍쐬�E�ҏW
�@CMS�t�@�C���Ƃ��āALETTER DATA A1 ���쐬����B�t�@�C����1��ʂɎ��܂�s���ł���A���e�A�\�����͎��R�ł���B�Ⴆ�A�p����[�}���̎莆�A���z���ł��悢���A�p�������g���ĕ`�����}�`�A�G�ł��悢�B�Ƃɂ����AXEDIT���g���Ċe���ŃI���W�i���e�B�[������e�̃t�@�C�����쐬���Ă݂邱�ƁB�쐬�����t�@�C���́A�[���L�[�{�[�h��(�[�W���)�L�[�������āA��ʂ���������܂邲�ƃv�����^�Ƀn�[�h�E�R�s�[���Ƃ邱�ƁB
�s�q���g�F�啶���E�������������Ďg�p���Ă���̂ɁA�啶�������ŕ\������Ă��܂��悤�ȏꍇ�A�t�@�C���ɑ啶���E�����������݂���������AXEDIT�ҏW��ʂ̃R�}���h�s��
�@�@�@====> SET CASE Mixed(���s)
�Ɠ��͂���Ƃ悢�B�t
7.2�@�t�@�C���̃R�s�[�Ɠ]�� �@�t�@�C�� PROFILE EXEC �͉ϒ��̃t�@�C���ł��邱�Ƃ�FILELIST�R�}���h�Ŋm�F����B����� PRO DATA A1 �Ƃ����Œ蒷�̃t�@�C���ɃR�s�[���ĕۊǂ���B���̌�A���̃t�@�C�� PRO DATA A1 �����[�U�[��=________ �ɓ]������B
�@�{��������Ƃ��Ă���Ɋw�K��i�߂�ǎ҂̂��߂ɁA�ǎ҂���r�I���肵�₷�����ǂ݂₷���悤�ɁA�a���̃e�L�X�g(�|����܂�)��V�������ɗ��Ă������B