
J. G. MarchとH. A. Simonの書いた Organizations という本がある。出版されたのは1958年、私の生まれた翌年である。近代組織論の金字塔的業績であり、いまや組織論の古典であるが、翻訳が出たのは原著出版後二十年もたった1977年、私が大学の学部学生の頃であった。その時は評判を聞いて一読してはみたものの、たいして印象も残らなかった。しかし、大学院に入り、多少なりとも勉強をしてから読み直してみて、そのバックグラウンドの広さにようやく気がついて唖然とした。統計的決定理論、ゲーム理論、経済学、心理学、行政学、社会学、そしてもちろん経営学の分野で、その後咲き乱れることになる大輪の花々の種子が組織論という鞘の中に埋め込まれている。そんな感じの本である。特に統計的決定理論との連続性には新鮮な驚きがあった。近代組織論は決定理論の理解なくしては語れない。この本との再会を果たして、私は自分の専門分野を決めた。
そして、本来の守備範囲である経営学の分野で、近代組織論ではいわばかくし味的存在であった統計的決定理論を前面に打ち出した組織研究をするようになった私は、後になって、大学院時代に統計的決定理論のまともな授業、演習に参加する機会に恵まれたこと自体、とてつもなく幸運なことであったことを知らされた。
こんな幸運に巡り合うことができたという感謝の気持ちが、本書執筆の根底にある。私の感じた新鮮な驚きをどれだけ伝えることができるだろうか。統計的決定理論と近代組織論の連続性を一つの流れとしてはっきり見えるようにできるだろうか。とにかく、一見かなり距離のある両者を1冊の著書にまとめる作業に着手したわけである。
本書を貫くのは、組織と人間に対する私の思いである。つまり、(i)人間は限られているとはいえ合理的に意思決定を行なうことができる。(ii)それを可能にするのが組織という装置であり、これを使って環境への適応をはかっている。しかし、(iii)人間は合理性に閉じ篭って生きているわけではない。大きな問題にぶつかって立往生したり、チャレンジしたりを繰り返していく。この(i)(ii)(iii)が、そのまま第I部、第II部、第III部のモチーフとなっている。
しかし、こうしたことを何らかの意味で哲学的にあるいは思想的に説こうというわけではない。現実の組織の中で起こっていることを説明するために、数学を使った抽象的なモデルや概念といった理論的な骨組みに、実際に組織現象を観察し、調べてわかった経験的事実を肉付けしていくと、自然とこうしたストーリーになるというだけのことである。その意味では、従来の経営組織論の本とも意思決定論の本ともかなり趣の異なる内容の本になったと思っている。
本書は草稿段階で、何度か大学での講義ノートとしての使用を経ており、文科系も含めて高校卒業程度の数学的予備知識があれば理解できるような工夫に努めたつもりである。確率の話が入ってくるところでは、コンピュータ言語BASICを使ったコンピュータ・シミュレーションを行ない、そのプログラムも記載している。プログラムはできるだけ簡単になるように工夫しているし、BASICはパソコンにスタンドアロンでも搭載されているケースが多いので、パソコンなどをお持ちの読者は、ぜひ一度自分でシミュレーションを楽しんでみることをお勧めする。確率の概念や何万回、何十万回の試行といったものに対する実感が湧いてくるはずである。
また数学的導出がいかに正しくとも、その結論が現実の組織現象と矛盾するのでは、そのモデルの前提や仮定が間違っていると判断せざるを得ない。組織現象の数理モデルを考える場合には、そういった厳しさが常に要求される。そこで本書では、組織の話が単なる数式やモデルの話で終ってしまわないように、私がこれまで手掛けてきた調査のデータを利用して、できるだけ現実の組織の姿、組織現象と結び付けるようにしている。そのために、常識的に理解可能な範囲での統計分析を行なっている部分もあるが、基本的には統計学の知識がなくても理解できるようになっているはずである。それでも、こうした統計分析に興味のある読者は、手元にある初歩的な統計学テキストあるいは拙著『経営統計入門-SASによる組織分析』(東京大学出版会, 1992)を参照してほしい。また、調査データを用いた組織分析に興味のある読者は拙著『ぬるま湯的経営の研究』(東洋経済新報社, 1993)に、こうした組織分析の実例が詳述されているので、あわせて参考にしてほしい。
冒頭にも記したように、本書は幸運な巡り合わせの中から生まれた。筑波大学大学院時代に、自らは経営学者でありながら、私に統計的決定理論をはじめとする数理的な専門科目を勉強するように強く勧めてくださった指導教官である高柳暁先生。そして副指導教官まで引き受けていただいて統計的決定理論を文字通り一から指導してくださった松原望先生(現在、東京大学教授)には、この場をお借りして心から御礼申し上げたい。
さらに、本書の執筆計画は、私の東北大学経済学部在職中に立てられたが、当時、原澤芳太郎先生(現在、東京理科大学教授)の研究室で時として深夜まで御専門の意思決定論と経営組織論について伺った話が、私に確信を抱かせ本書執筆のきっかけとなった。また武藤滋夫先生にもゲーム理論と決定理論の関係について疑問が氷解する経験を何度もさせていただいた。改めて感謝の意を表させていただきたい。
その後、私の職場が東京大学教養学部に変わったが、教養学科で担当した意思決定論の授業は私の考えをまとめる良い機会となった。助手時代を含め、こうした著書をまとめる知的自由を与えていただいた東京大学教養学部に感謝したい。本書がもとにしている調査データの収集に当っては、日本電信電話公社(現在の日本電信電話株式会社)及び財団法人日本生産性本部経営アカデミーの援助と協力が得られたことにも謝意を表したい。本書の執筆を引き受けてから六年が経過しているが、その間、朝倉書店の柏木信行氏には辛抱強く励ましていただいた。この場を借りて御礼申し上げたい。最後になるが、本書の執筆のために何度となく休みの予定をあきらめてくれた妻敦子と息子伸之に心から感謝したい。
1993年8月
高橋伸夫
本書の流れを全体として理解しておいてもらうために、まずは、誰もが知っている簡単なゲーム、ジャンケンを材料としてメニュー紹介をしておこう。
いまA君、B君の二人がジャンケンする場面を想定してみる。二人の出す手はもちろん
グー、チョキ、パー
のどれか一つで、二人の出す手の組合せによって勝負がつくことは御存知のとおりである。A君の星取り表を作ってみれば、表0.1(a)のようになる。一方、B君の星取り表は、ちょうどこれと裏返しになり、表0.1(b)のようになる。
表0.1 星取り表
(a) A君の星取り表
| A君の手 | B君の手 | ||
|---|---|---|---|
| グー | チョキ | パー | |
| グー | △ | ○ | ● |
| チョキ | ● | △ | ○ |
| パー | ○ | ● | △ |
(b) B君の星取り表
| A君の手 | B君の手 | ||
|---|---|---|---|
| グー | チョキ | パー | |
| グー | △ | ● | ○ |
| チョキ | ○ | △ | ● |
| パー | ● | ○ | △ |
ところで、A君、B君の二人はただジャンケンしていてもつまらないというので、ジャンケンで勝った方が、負けた方から100円もらえることにした。すると、もう星取り表は単なる勝敗ではなく、表0.2のような金額を書き込んだ利得表になる。A君の利得表は表0.2(a)のようになり、B君の利得表はちょうどこれと裏返しの表0.2(b)のようになる。当然のことながらA君とB君の利得の合計(つまり和)は0になる(だからゼロ和ゲームという)。
表0.2 利得表
(a) A君の利得表
| A君の手 | B君の手 | ||
|---|---|---|---|
| グー | チョキ | パー | |
| グー | 0 | 100 | -100 |
| チョキ | -100 | 0 | 100 |
| パー | 100 | -100 | 0 |
(b) B君の利得表
| A君の手 | B君の手 | ||
|---|---|---|---|
| グー | チョキ | パー | |
| グー | 0 | -100 | 100 |
| チョキ | 100 | 0 | -100 |
| パー | -100 | 100 | 0 |
もし仮にB君が、純粋に「パーだけを出す」という戦略(これを純戦略という)を立てたとしよう。これに対してA君はチョキを出す戦略で勝つことができる。B君の出す手がグーでもチョキでも同じこと、純戦略である限り、A君にはそれに対抗する戦略が立てられる。一体B君はどうしたら良いのだろうか。
それでは、パーだけを出すというのではなく、10回に1回はグーを出す戦略に変更しようか。しかし、それでもA君のチョキを出す戦略に対して、B君は1勝9敗ペースの大敗を喫することになる。つまり、B君がグー、チョキ、パーのどれか一つの手にこだわりをもち続ける限り、A君はB君に勝越すことができるのである。そこで考えられるのは、B君はグーもチョキもパーも同じ比率つまり1/3ずつ混ぜ合わせて出していくという戦略である(これを混合戦略という)。こうなってしまうと、A君もB君となんとか勝敗を分けるために、やはりグーもチョキもパーも同じ比率1/3ずつで出していくしかない。
もちろん自分の出す手を相手に教えてからジャンケンをすることはないのだが、ここまでくると、たとえ互いに相手の混合比率を知っていたとしても、AB両君ともこの混合比率を変えることはないだろう。つまりこの状態でゲームは均衡しているのである。実は、この均衡は単なる戦略のレベルの均衡にとどまらない。その戦略を決める意思決定原理のレベルでも「均衡」することになるのである。こうしたことを厳密に議論するためにゲーム理論が登場することになる。
こうなってしまうと、A君もB君も、自分の壷の中にグー、チョキ、パーの印のついている玉をそれぞれ同数入れておいて、審判役の人がA君の壷とB君の壷からそれぞれ1個ずつ玉を取り出して、勝敗を判定しても同じことになる。つまり、くじを引くのと同じである。このように結果として得られる利得が確率をともなっている場合、利得はどのように評価すべきなのだろうか。例えば、均衡しているときは、A君もB君もどちらが有利ということはなかった。ということはA君もB君も損得なしということになっているはずだ。そうでもなければ、ジャンケンはこれほど広くは普及しなかったであろう。しかし、そのことをどうやって確かめるのだろうか。実はこのことは、厳密には期待効用として効用理論の中で研究される。
ところで、仮にB君が「パーだけを出す」と確固たる信念をもって行動するとして、A君はどうやってそれを知ることになるのだろう。実際には、B君がパーをよく出すということはA君も知っていることが多い。つまり、このときA君は、B君の混合戦略の混合比率が1/3ずつではなく、パーにやや重きを置いたもの、例えば確率分布(1/4,1/4,1/2)であることを知っていることになる。こうした確率が存在することは主観確率の理論で取り扱われる。
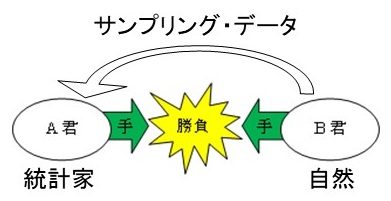
しかし、これだけでは心許ないときには、A君はB君についての情報収集を行なう。一番いいのは、実際に勝負に入る前に何回か試しジャンケン(これを試行または実験という)をしてみて、A君の手の出し方の頻度を見るのである。これは統計学でデータを取ることあるいはサンプリングすることと同じである。ただし、統計的状況では、試しジャンケンによってB君の出す手がA君の出す手に影響されてしまっては困る。そこで、B君は泰然として統計家A君のスパイ行為を黙認する懐の深い自然だと考えるのである。こうして、統計的状況は、統計家対自然という2人ゼロ和ゲームとして定式化され、ここに統計的決定理論が誕生する。その際のデータの利用に際してはベイズの定理が活躍することになる。
もっとも、本当にB君のことを知ろうと思ったら、A君は四六時中B君を徹底的にマークし、ジャンケンをしつこくせまり、記録を丹念に取り、詳細に分析し……などという行動を取らねばならない。しかしこれでは、A君は体がいくつあっても足りなくなる。多分それは不可能であろう。あるいは物理的には可能であっても、たかが100円掛けのジャンケンのために……、経済的には割に合わないことは目に見えている。A君が全知全能の人ならば心配はないが、人間の合理性には自ずと限界があるのである。
ところがA君は、B君のごく親しい友人のC君から耳よりな情報を入手した。B君はかつてC君に「僕はパーしか出さないことに決めているんだ」と話していたというのである。そこでC君は自分がB君とジャンケンをするわけにはいかないので、A君にこの情報を提供し、もうけた分は2人で山分けにしようと持ちかけたわけである。いわばB君についての権威であるC君からの情報なので、A君はそれを受け入れ(つまり権威あるものとして信用し)、この情報を前提として、意思決定を行なうことにしたのであった。つまり、「チョキを出す」ことにしたのである。(ただし、実際の経済活動では、こうした取引はインサイダー取引と呼ばれ、禁じ手にされているはずであるが……。) そしてA君(というより組織)はB君に対して確実に勝利することになったのである。たった2人の連携プレイとはいえ、これは組織の勝利であった。限定された合理性しかもたない人間が、組織的な意思決定過程の中でそれをある程度克服したささやかな事例である。ここに近代組織論が誕生することになる。
図0.1 ゲームから組織へ
(a) 2人ゲーム

(b) 統計的状況(統計家対自然)
(c) 組織的状況(組織対環境)
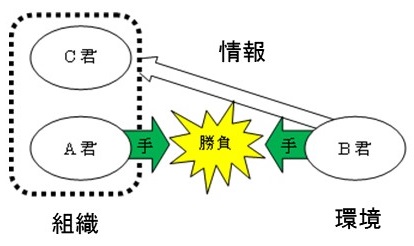
とはいっても、組織さえ作ればすべてが丸く収まるというわけではない。このA君とC君の組織でも、仮にC君がこの情報の入手のための必要経費として200円を要求したらどうなるだろう。つまり情報コストは組織の成否を左右する。さらに、いまの例では情報が得られれば、A君のとる手が確実にわかってしまうが、一般には対戦相手がどの手をとるのかについては不確実性がともなうのが普通である。こうしたときには、組織の形態は今のままで良いのだろうか。組織を通じての情報の収集の仕方はこれで良いのか、そして、A君とC君の仕事の分担はこれで良いのか、といったことが少なくとも経済的、コスト的には問題となってくる。これが環境の不確実性への適応を考えた組織設計の問題である。
さらに、確かにこのときはA君とC君の2人は小さな組織としてうまく機能したが、人間が2人いればいつでも組織となるわけではない。組織として機能するためにはたった2人の集団とはいえ、2人の間にコミュニケーションがなくてはいけないし、もっと重要なことは、2人が共通の目的(先ほどの例では「B君にジャンケンで勝ち、100円もうけること」)をもち、この目的に対して積極的に協働する意欲をもっていることである。これが組織成立の3条件と呼ばれるものである。このように集団を組織として機能するようにせしめることを組織活性化という。組織が活性化していなければ、とりうる組織形態にも、当然、制約が生じることになり、環境適応がうまくいかないことになる。
もっとも、このA君とC君の組織は、B君以外の人に対してはいたって非力な存在である。特に、ジャンケンにおいて独自のノウハウとデータ収集、分析能力を誇るD君と対戦しては、下手すると大損する可能性がある。D君と対戦するにはA君はまだ弱すぎるのである。そこでA君は、D君が近付いて来ると、ジャンケンの話は一切口にしない。ジャンケンを持ちかけられても、じっと聞き流し、D君があきらめて、別の対戦相手を探しにその場を立ち去るまで、やり過ごすのである。
こうして、もうけるために、A君(とC君の組織)は、D君を避け、B君とのみ対戦を続けることになる。もうけることだけが目的ならば、これが一番良いのだが、A君はこうして純粋なB君に勝ち続けることに、何か物足りなさを感じ、満足できない自分に気がついた。とうとうある日、A君はB君に真実を打ち明け、今度は知恵を絞って、D君にチャレンジすることにしたのである。いくら強いといってもD君にも癖はあるだろうし、D君自慢のノウハウだって、わかってしまえばその裏をかいて勝つ方法があるかもしれない……。ゲームのような状況にあってさえ、人を動機づけ、つき動かすものは単なる損得以上の何かである。ましてや人にとって、仕事は単に、くじを引く以上の何かである。
本書でこれから取り扱うテーマをメニュー紹介風にジャンケンを材料として説明するとざっとこういうことになる。もちろん、もともとはジャンケンなどではなく、実際の組織現象を材料とした話であるし、それぞれの説明の背景には、かなり抽象的で厳密な理論も存在している。これから本格的に議論を進めていくことになるわけだが、以上のメニュー紹介を踏まえて、組織論の中で決定理論の果たす役割を本書の流れの中で理解して欲しい。
ゲーム理論は第二次世界大戦後に続々と誕生する社会科学の様々な研究領域に、アイデアや概念体系の点で多大の影響を与えている。本書の主要関心である、統計的決定理論や近代組織論(特にSimon以降)もその生成過程において、ゲーム理論の強い影響下に置かれていたことは学説史的な事実である。本書では、近代組織論のエッセンスを理解するために、まずは第Ⅰ部 (第1章~第3章) で、簡単なゲーム理論から始め、ゲーム理論や決定理論の中で意思決定がどのように扱われているのかを見ることにしよう。その上で、第Ⅱ部 (第4章~第6章) でそれらの理論が組織論の中でどのように展開していったのか、どのような応用が可能なのかについて見ることにする。そして第Ⅲ部 (第7章~第8章) では、実際の組織現象で決定理論の枠をはみ出した部分について、決定理論の側からその諸概念を用いて、どのようにはみ出しているのかを考えてみることにしよう。
意思決定について体系的に取り扱う試みは、ゲーム理論と呼ばれる領域から始まったといっていいだろう。実際、意思決定を分析する決定理論は、このゲーム理論から派生して生まれてくることになる。そこでこの章では、ゲーム理論について簡単な導入をはかった上で、ゲーム理論の中で意思決定やそこに至る意思決定原理をどのように扱うことができるのかを考えてみることにしよう。
序章で例として取り上げたジャンケンをはじめとして、将棋、チェス、トランプなどの様々なゲーム(game)は、複数のプレイヤーが、各々の行動を規定する一組の規約、ルール(rule)に従ってプレイするものである。たとえば先ほどのジャンケンをより詳細に観察してみると、2人で行なう最も基本的な1回限りのジャンケンでは、2人のプレイヤーがグー、チョキ、パーという3種類の手の中から一つの手を選択し、その選択(choice)の結果を文字どおり「手」で表現して提示するという動作から成り立っているわけである。そして、手の組合せによって2人のプレイヤーの勝敗がどう定まるのかが事前に取り決められている。
そこでまず、こうしたゲームのルールを構成する基本的な要素について、概念的に整理しておこう。
以上のようなルールの基本的要素によって記述されるゲームにおいて、ゲームの理論では、まず各プレイヤーは自分の受け取る利得を最大にしようとして戦略を選択すると考える。この前提に立った上で「ゲームを解く」ことを考えるのである。ゲームを解くというのは、簡単にいうと、ゲームの均衡点(equilibrium point)とそのときの均衡利得(すなわちゲームの値)を求めることをさしている。『広辞苑 第3版』(1983)によると、均衡とは二つ以上の物・事の間につりあいが取れていることとされるが、ゲームにおいても、ゲームの均衡点は何らかの意味でつりあいのとれている各プレイヤーの戦略の組であり、ゲームの値とはその均衡点における各プレイヤーの利得の組をさしている。
それでは、2人ゲームのルールについて、定式化してみよう。
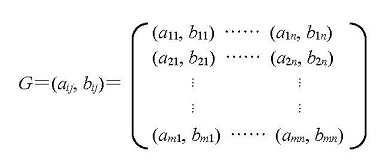
さらに、この形式をふまえると、戦略と利得の関係は、表1.1のような利得表でも表すことができる。例えば、序章のジャンケンの例をこの利得表の形に書き直すと、表1.2のようになる。
表1.1 利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | ||
|---|---|---|---|
| 1 | …… | n | |
| 1 | (a11, b11) | …… | (a1n, b1n) |
| 2 | (a21, b21) | …… | (a2n, b2n) |
| : | : | : | |
| m | (am1, bm1) | …… | (amn, bmn) |
表1.2 序章のジャンケンの利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | ||
|---|---|---|---|
| 1 (グー) | 2 (チョキ) | 3 (パー) | |
| 1 (グー) | ( 0, 0) | ( 100,-100) | (-100, 100) |
| 2 (チョキ) | (-100, 100) | ( 0, 0) | ( 100, -100) |
| 3 (パー) | ( 100, -100) | (-100, 100) | ( 0, 0) |
このように定式化したとき、ゲームの均衡点は次のように定義される。すなわち、
f1(i*, j*)= maxi∈Π1 f1(i, j*) (1.1)
f2(i*, j*)= maxj∈Π2 f2(i*, j) (1.2)
を満たすとき、(i*, j*) を均衡点(equilibrium point)あるいはナッシュ均衡点(Nash equilibrium point)といい、この均衡点での利得 ( f1 (i*, j*), f2 (i*, j*)) を均衡利得という。たとえば、表1.3のような利得表を考えれば、戦略の組 (2,2) がナッシュ均衡点であり、ゲームの値は (4,4) となることがわかる。
表1.3 ナッシュ均衡点
| プレイヤー1 | プレイヤー2 | |
|---|---|---|
| 1 | 2 | |
| 1 | (2, 2) | (0, 6) |
| 2 | (6, 0) | (4, 4) |
いまナッシュ均衡点に双方のプレイヤーがいるとしよう。仮に片方のプレイヤーがそのままで、もう一方のプレイヤーが戦略を変えるとすると、ナッシュ均衡点の定義から、戦略を変えたプレイヤーの方が利得を減らし、損をすることになる。したがって、この均衡点からどちらのプレイヤーも離れようとはしない。つまり、つりあいがとれ、安定していることになる。だから均衡点と呼ばれるわけである。このように、他のプレイヤーが各自の戦略から逸脱(deviate)しないことが所与とされるときに、いかなるプレイヤーも自分の戦略から逸脱するインセンティブをもたないならば自己拘束的(self-enforcing)であるといわれる。
このように均衡点の定義だけを見ていると、ゲームの均衡の概念は非常にすっきりしたものに感じられるが、実は個々のケースでは、どうもすっきりとは納得のできない場合もある。そのうち特に有名なケースを二つほど例としてあげておこう。
例1.1 囚人のジレンマ(prisoner's dilemma)
2人の共犯の容疑者、囚人1と囚人2とが逮捕され、分離された上で別々に尋問を受けている。もし2人とも自白した場合には、懲役8年の刑になるが、2人とも自白しなければ、検察側も些細な犯罪しか立証できないので、懲役1年の刑で済むことになる。検察側は、2人の容疑者に自白を促すために、どちらか1人だけが自白した場合には、自白しなかった1人には、この罪での最高刑の懲役10年を求刑するが、自白した1人は検察に協力したということで懲役はないという司法取引を提示した。さて、囚人1と囚人2はどのような行動をとるのであろうか。この場合、刑期は負の利得なので、刑期にマイナスをつけて利得表を作成すると、表1.4のようになる。
表1.4 囚人のジレンマ
| 囚人1 | 囚人2 | |
|---|---|---|
| 自白しない | 自白する | |
| 自白しない | (-1, -1) | (-10, 0) |
| 自白する | ( 0, -10) | ( -8, -8) |
この利得表からもわかるように、均衡点は (自白する, 自白する) という戦略の組で、ゲームの値は (-8, -8) ということになる。ところが、実は (自白しない, 自白しない) をとることができれば、利得は (-1, -1) となって、二人の囚人にとってはるかに望ましいはずなのである。この (自白しない, 自白しない) のように、他のプレイヤーの利得を減少させることなく、あるプレイヤーの利得を増加させることができないような戦略の組はパレート最適(Pareto optimum)と呼ばれる。その意味では、(自白しない, 自白しない) は望ましい状態のはずなのに、この囚人のジレンマと呼ばれるケースではナッシュ均衡点にはならない。そして、このケースでのナッシュ均衡点はパレート最適にはなっていないのである。
例1.2 両性の闘い(the battle of the sexes)
1組の男女の間のゲームで、男の方はボクシングの試合を見に行きたいと思っているし、女の方はバレエを見に行きたいと思っている。ただし、2人は自己中心的な性格ではあるのだが、そこは恋人同士、必要ならば自分が見たいものを犠牲にしてでも2人で一緒にいたいとは思っている。こうした状況を利得表で表すと、表1.5のようになる。(ボクシング, バレエ) と (バレエ, ボクシング) の利得は逆ではないかと思われるかもしれないが、実はここでは、我を通してしまったことへの「後悔」を反映した利得になっている(§1.2eを参照のこと)。
利得表からもわかるように、このゲームには二つのナッシュ均衡点が存在している。一つは (ボクシング, ボクシング) という戦略の組であるし、もう一つは (バレエ, バレエ) という戦略の組である。しかも、いずれもパレート最適である。しかしこのゲームには大きな問題点がある。一体、この男女のカップルはどのようにして、どちらのナッシュ均衡点が選ばれるのかを知るのであろうか。もし男の方が (ボクシング, ボクシング)、女の方が (バレエ, バレエ) が均衡点だと思い込んでいたら、結局選択されるのは (ボクシング, バレエ) であり、2人は最悪の結末を迎えることになる。
表1.5 両性の闘い
| 男 | 女 | |
|---|---|---|
| ボクシング | バレエ | |
| ボクシング | ( 2, 1) | (-5, -5) |
| バレエ | (-1, -1) | ( 1, 2) |
以上のように、均衡点がどれかはわかったものの、その均衡点が果たして達成可能なのか、そしてもし可能だとして、それはプレイヤーがどのように考えて行動したときに達成されるのか、つまりどのような意思決定原理に則って行動したときに達成されるのかについては、まだ明らかではない。そこでここでは、プレイヤーの行動を意思決定原理の側面から考えてみることにしよう。
意思決定原理を簡潔に説明するために、本書ではこれ以降、ゲームをより単純化して、ゼロ和ゲームに限定して話を進めることにしよう。いま2人ゲームのうち、特に2人のプレイヤーの利得 f1 (i, j)、f2 (i, j) の和が常に0であるような場合、すなわち、
f1 (i, j)+ f2 (i, j)=0
であるとき、このゲームはゼロ和2人ゲーム(zero-sum two-person game)と呼ばれる。ゼロ和2人ゲームの場合には、
f1 (i, j)=-f2 (i, j)
と一方のプレイヤーの利得は、他方のプレイヤーの利得の符号をひっくり返したものになるので、2人の利得を両方とも併記して書く必要はない。そこで、
aij=f1 (i, j)=-f2 (i, j)
とおいて、戦略と利得との関係を次のような行列の形で表現することができる。この行列は利得行列(payoff matrix)とよばれ、このような行列の形で表現できることから、ゼロ和2人ゲームは行列ゲーム(matrix game)ともよばれる。
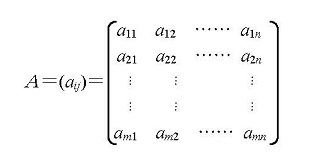
表1.6 2人ゼロ和ゲームのプレイヤー1の利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | |||
|---|---|---|---|---|
| 1 | 2 | …… | n | |
| 1 | a11 | a12 | …… | a1n |
| 2 | a21 | a22 | …… | a2n |
| : : | : : | : : | : : | |
| m | am1 | am2 | …… | amn |
そこで、ゲームをする際にプレイヤーが依拠するであろう意思決定原理について考えることにしよう。これについては、既に先人達が知恵を絞って考案しているので、この節ではその中でも有名ないくつかの意思決定原理について紹介してみよう。なお説明の便宜上、ここではプレイヤー1の意思決定原理を考えることにする。ゼロ和2人ゲームなので、プレイヤー2の意思決定原理は式の中の大小関係を逆にしたものになる。
もともとゲーム理論で考えられていたのがマクシミン原理(maximin principle)である。後にWald (1950)が決定理論を構築する際に取り上げたために、ワルド(Abraham Wald)のマクシミン原理 (Wald's maximin principle)ともよばれるようになった。この意思決定原理では、戦略 i をとったときの最悪の可能な結果、つまり利得が一番小さくなる結果
si=minj aij
を考える。これは戦略 i の保証水準(security level)と呼ばれ、戦略 i は少なくともこの si の利得を保証していることになる。このとき、マクシミン原理は
sk=maxi si=maxi minj aij
のように最大の保証水準をもたらす戦略 k を選ぶという意思決定原理である。
たとえば、表1.7(a)のような利得表が与えられたとき、プレイヤー1の各戦略の保証水準は表1.7(b)のようになる。したがって、マクシミン原理に則ったプレイヤー1の戦略は 1 ということになる。
表1.7 ワルドのマクシミン原理
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 si | |
|---|---|---|---|
| 1 | 2 | ||
| 1 | 4 | 6 | 4 |
| 2 | 2 | 0 | 0 |
このように、マクシミン原理は各戦略をとったときに起こりうる最悪の事態を考えて戦略をとるという意味では、悲観的な(pessimistic)意思決定原理である。それに対して、これから扱うマクシマクス原理(maximax principle)は、各戦略をとったときに起こりうる最良の事態を考えて戦略をとるという意味で、楽観的な(optimistic)意思決定原理である。つまり、まず戦略 i をとったときの最良の可能な結果
oi=maxj aij
を考える。これは戦略 i の楽観水準(optimism level)と呼ばれる。このとき、マクシマクス原理は
ok=maxi oi=maxi maxj aij
のような最大の楽観水準をもたらす戦略 k を選ぶという意思決定原理である。
たとえば、先ほどの表1.7(a)とまったく同じ利得表、表1.8(a)が与えられたとき、プレイヤー1の各戦略の楽観基準は表1.8(b)のようになる。したがって、マクシマクス原理に則ったプレイヤー1の戦略は 1 ということになる。
表1.8 マクシマクス原理
| プレイヤー1の戦略 | プレイヤー2の戦略 | 楽観水準 oi | |
|---|---|---|---|
| 1 | 2 | ||
| 1 | 4 | 6 | 6 |
| 2 | 2 | 0 | 2 |
表1.9 ハーウィッツの楽観・悲観指数原理
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 si | 楽観水準 oi | αsi+(1-α) oi | |
|---|---|---|---|---|---|
| 1 | 2 | ||||
| 1 | 4 | 6 | 4 | 6 | 4α+6-6α=6-2α |
| 2 | 2 | 0 | 0 | 2 | 2-2α |
この例のように、もともとマクシミン原理でも、マクシマクス原理でもとるべき戦略が一致しているような場合には、α の大きさは意味をもたないが、§1.2.fで後述する例のように、α の大きさが決定的に重要になる場合もある。といっても、その肝心の自分の楽観・悲観指数の大きさはどのくらいなのだろうか。もし、自分の α がどのくらいの大きさであるかを知りたければ、次のごく単純な実験を行なえばよいとされている(French, 1986)。
実験1.1 いま表1.10のような利得表のゲームで、自分がプレイヤー1だとしよう。このとき、戦略 1 と戦略 2 が無差別になる v の値を求めてみよう。
表1.10 楽観・悲観指数を求める利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 1 | 0 |
| 2 | v | v |
この実験の結果から楽観・悲観指数αを求める方法について説明しておこう。もしある v の値で戦略 1 と戦略 2 が無差別ならば、表1.11(b)からもわかるように、1-α=vであるはずであるから、α=1-v と求まることになる。
このとき、v の値は0と1の間の値になっているはずである。なぜなら表1.10で与えられた利得表において、仮に v=1 とすると、今度は表1.12(a)のようになって、これは明らかに戦略 2 を選ぶことになり、仮に v=0 とすると、今度は表1.12(b)のようになって、これは明らかに戦略 1 を選ぶことになるはずだからである。そこで問題は、v が0から1の間のどの値のときに戦略 1 と戦略 2 が無差別になっているかということになる。これは主観の問題なので、もちろん正解や不正解ということはない。この機会に自分で実際にやってみることをすすめる。
表1.11 楽観・悲観指数を求める
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 si | 楽観水準 oi | αsi+(1-α) oi | |
|---|---|---|---|---|---|
| 1 | 2 | ||||
| 1 | 1 | 0 | 0 | 1 | 1-α |
| 2 | v | v | v | v | αv+(1-α) v=v |
表1.12 両極端のケース
(a) v=1
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 1 | 0 |
| 2 | 1 | 1 |
(b) v=0
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 1 | 0 |
| 2 | 0 | 0 |
ただし、この方法には大きな問題点がある。そのことは次の実験1.2をやってみるとよくわかる。利得の金額の単位が異なるときに、無差別となる v の値が異なることは十分に予想されることである。(詳しくは第2章の効用関数のところで後述する。)
実験1.2 既に行なった実験1.1では利得表の利得の単位について何も触れていなかったが、今度は表1.10の数字を金額であると考え、(1) 利得の単位が十円、(2) 利得の単位が万円、(3) 利得の単位が億円、の三つのケースについて、それぞれvの値と楽観・悲観指数αを求めてみよう。
「逃した魚は大きい」「後悔先に立たず」などとよくいわれるが、このような後悔(regret)を決定に先だって考え、それから意思決定を行なおうというのが、サベージ(Leonard J. Savage)の考えたミニマックス・リグレット原理(Savage's minimax regret principle)である(Savage, 1951)。
いまプレイヤー1は相手のプレイヤー2がどんな戦略をとるかわからないので、仮に、プレイヤー2がある戦略 j をとると仮定しよう。その戦略 j に対して最良の戦略をプレイヤー1がとっていれば得られたはずの利得 maxi aij と実際にとる戦略 t の利得 atj との差をリグレット(regret)と定義する。すなわち、
rtj=maxi aij-atj
そこで、利得行列の各 atj をこのリグレット rtj で置き換えた利得行列を考え、これについてワルドのマクシミン原理を適用することを考えるのである。ただし、リグレットは利得でなく、「損失」なので、最小ではなく、最大のリグレット
ρi=maxj rij
を保証水準と考え、
ρk=mini ρi=mini maxj rij
のような最小の保証水準をもたらす戦略 k を選ぶという意思決定原理である。
たとえば、これまでとまったく同じ利得表、表1.13(a)が与えられているとき、プレイヤー2の各戦略に対して最良の戦略をプレイヤー1がとっていれば得られたはずの利得は、利得表の縦の各列の最大値に相当するので、それは表1.13(a)に示されているようになる。この値をもとにして、プレイヤー1のリグレット表を作ると、表1.13(b)のようになる。この表1.13(b)に関して、プレイヤー1の各戦略の保証水準は表1.13(c)のようになるので、したがって、ミニマックス・リグレット原理に基づくプレイヤー1の戦略は最小の保証水準をもたらすということで、やはり戦略 1 ということになるのである。
表1.13 サベージのミニマックス・リグレットの原理
(a)利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 4 | 6 |
| 2 | 2 | 0 |
| max | 4 | 6 |
(b)プレイヤー1のリグレット表
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 ρi | |
|---|---|---|---|
| 1 | 2 | ||
| 1 | 0 | 0 | 0 |
| 2 | 2 | 6 | 6 |
これまで扱ってきた例では、どの意思決定原理にしたがっても、同じ戦略を選ぶ結果になった。しかし、常にそうなるとは限らない。それぞれの意思決定原理がそれぞれ全く異なる戦略の選択に導くこともある。
例題1.1 表1.14の利得表について、これまで扱ってきた4種類の意思決定原理に則ってプレイヤー1の戦略を選択してみよ。ただし、楽観・悲観指数は0.7とする。
表1.14 例題の利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 1 | 2 | 2 | 2 | 2 |
| 2 | 0 | 8 | 0 | 0 |
| 3 | 2 | 6 | 1 | 1 |
| 4 | 4 | 6 | 4 | 0 |
《解答》表1.15から、次のような意思決定が行なわれる。
表1.15 例題1.1の解答
(a)利得表
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 si | 楽観水準 oi | αsi+(1-α) oi | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 0 | 8 | 0 | 0 | 0 | 8 | 8-8α=2.4 |
| 3 | 2 | 6 | 1 | 1 | 1 | 6 | 6-5α=2.5 |
| 4 | 4 | 6 | 4 | 0 | 0 | 6 | 6-6α=1.8 |
| max | 4 | 8 | 4 | 2 | |||
(b)プレイヤー1のリグレット表
| プレイヤー1の戦略 | プレイヤー2の戦略 | 保証水準 ρi | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 2 | 6 | 2 | 0 | 6 |
| 2 | 4 | 0 | 4 | 2 | 4 |
| 3 | 2 | 2 | 3 | 1 | 3 |
| 4 | 0 | 2 | 0 | 2 | 2 |
この例題からもわかるように、こうなってくると、どの戦略が選択されるかは、採用される意思決定原理によってまったく異なるわけで、どの意思決定原理を採用するかがそれ自体大問題となる。そして、ある意思決定原理に則ってある戦略を選択したプレイヤーにとって、予想外の戦略を選択したプレイヤーがいかなる意思決定原理に則って意思決定を行なったのかを想像し、理解することは至難のわざということになる。よく日本人はプリンシプルがないと言われるが、これも本当にプリンシプルがないのかどうかは大いに疑問である。たとえもっていたとしても、それとは異なるプリンシプルに則って意思決定を行なう他の文化圏の人にとっては、表面に現れる意思決定や行動だけを見て、そこに至らしめる意思決定原理を想像し、理解することはほとんど不可能だからである。
それでは、どの意思決定原理に則って行動すれば均衡点に達することができるのだろうか。実は、均衡点の存在するゼロ和2人ゲームにおいては、2人のプレイヤーがマクシミン原理にしたがって行動するならば、均衡点に達することがわかっている。しかもどちらか一方のプレイヤーがマクシミン原理を意思決定原理として採用を決めると、他のプレイヤーもマクシミン原理を採用せざるをえなくなるというきわめて安定性の高い意思決定原理であることもわかっている。そこでここでは、まずゼロ和2人ゲームにおける均衡点の定義をしてから、そのことを証明してみよう。
ゼロ和2人ゲームは2人ゲームの特殊な場合であるから、ナッシュ均衡点の定義をそのまま適用することができる。f2(i, j)=-f1(i, j) のとき、ナッシュ均衡点の定義式(1.1)式、(1.2)式はそれぞれ
f1(i*, j*)= maxi∈Π1 f1(i, j*) (1.1')
f1(i*, j*)= minj∈Π2 f1(i*, j ) (1.2')
となるから、この両式を満たす (i*, j*) はゼロ和2人ゲームの均衡点ということになる。
このとき(1.1')式と(1.2')式とを f1(i*, j*) で結合すると、任意の i∈Π1, j∈Π2 について、
f1(i, j*)≦ f1(i*, j*)≦ f1(i*, j)
となる。実は、行列 A=(aij) において、任意の i, j について、
aij'≦ai'j'≦ai'j
が成立するとき、(i', j') をこの行列の鞍点(「あんてん」: saddle point)とよび、ai'j' を鞍点値(saddle point value)という。したがって、ナッシュ均衡点 (i*, j*) はゼロ和2人ゲームの利得行列の鞍点となっていることになる。利得行列に少なくとも一つ鞍点が存在すれば、その鞍点が均衡点であり、鞍点値はゲームの値である。このような均衡点が存在しているとき、このゲームは厳密に決定されるゲーム(strictly determined game)または閉じたゲーム(closed game)といわれる。
たとえば、表1.16(a)のような利得表のゼロ和2人ゲームでは、均衡点は戦略の組 (1, 1) であり、ゲームの値は 4 となっていることがわかる。しかし、鞍点つまり均衡点が常に存在しているわけではない。この利得表でも、表1.16(b)のように (1, 1) の利得の値を 1 に変えると、もはや鞍点は存在せず、プレイヤー1、プレイヤー2は矢印のように次々と戦略を変えていくことになる。
表1.16 鞍点とゲームの均衡
(a)鞍点の存在するゲーム
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 4 | 6 |
| 2 | 2 | 0 |
(b)鞍点の存在しないゲーム
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | 1 ↓ | ←6 |
| 2 | 2→ | ↑ 0 |
こうした鞍点が実はマクシミン原理によって達成されることがわかっている。次にこのことを証明しよう。マクシミン原理とは、自分が戦略 i をとったときに、最悪の場合でも得られる利得(=戦略 i についての保証水準(security level))を考え、この利得が最大となるような戦略を選択する意思決定原理であった。したがって、マクシミン原理にしたがったときに考えられる各プレイヤーの利得は、
プレイヤー1: v1=maxi minj aij
プレイヤー2: v2=minj maxi aij
ということになる。もっとも、この値が、そのままゲームの結果を表しているわけではない。もちろんゼロ和ゲームなので、プレイヤー2の実際の利得はこれにマイナスをつけたものになるわけだが、ここでは、プレイヤー2の利得はこの「支払う利得」の形で表しておくことにしよう。すると、v1とv2の間には、均衡点の存在の有無にかかわらず、次のような関係のあることがわかっている。
定理1.1 v1≦v2
《証明》まず任意の i', j' について
minj ai'j≦ai'j'≦maxi aij'
したがって、任意の j' について
maxi minj aij≦maxi aij'
がいえるので
maxi minj aij≦minj maxi aij □
実は、もし均衡点が存在すれば、すなわち鞍点 (i*, j*) が存在すれば、その鞍点は2人のプレイヤーがそれぞれマクシミン原理に則って戦略を選択するとき達成され、そのときはじめて v1=v2=ai*j* となる。均衡点が存在しないときには、v1とv2の間には乖離が生じているのである。そのことは先ほどの例でも表1.17のように簡単に示すことができる。
表1.17 鞍点と v1、v2
(a)鞍点の存在するゲーム(v1=v2)
| プレイヤー1の戦略 | プレイヤー2の戦略 | ||
|---|---|---|---|
| 1 | 2 | min | |
| 1 | 4 | 6 | 4=v1 |
| 2 | 2 | 0 | 0 |
| max | 4=v2 | 6 | |
(b)鞍点の存在しないゲーム(v1≠v2)
| プレイヤー1の戦略 | プレイヤー2の戦略 | ||
|---|---|---|---|
| 1 | 2 | min | |
| 1 | 1 | 6 | 1=v1 |
| 2 | 2 | 0 | 0 |
| max | 2=v2 | 6 | |
このことを証明してみよう。
定理1.2 (鞍点定理) v1=v2 となる必要十分条件は、この利得行列が鞍点をもつことである。
《証明》(十分性) いま (i*, j*) を鞍点とすると、定義から、任意の i, j について
(必要性) v1=v2 ならば、
定理の証明から、v1=v2 ならば v1=v2=ai*j* と、鞍点 (i*, j*) での利得の値に等しくなることがただちにわかる。すなわち、ゼロ和2人ゲームに均衡点が存在しているときには、各プレイヤーがマクシミン原理に則って戦略を選択すると、それが均衡点となるのである。
ゼロ和2人ゲームでは、一方のプレイヤーがマクシミン原理に則って戦略を選択している限り、もう一人のプレイヤーにとっても、マクシミン原理が最適な意思決定原理となる。なぜなら、マクシミン原理から逸脱することは、均衡点から逸脱する可能性を意味し、均衡点の定義から、戦略を変えたプレイヤーの方が利得を減らすことになるからである。したがって、マクシミン原理は、どちらか一方のプレイヤーが意思決定原理として採用を決めると、他のプレイヤーも採用せざるを得なくなる性質をもち、しかもその際には均衡点に達するというきわめて安定性の高い意思決定原理であるということができる。つまり戦略といういわば行動や決定のレベルで均衡点が存在しているだけではなく、その意思決定に至る手前の意思決定原理のレベルでも均衡が存在していることになる。
このように、均衡点が意思決定原理と明快な関係をもっているのが、ゼロ和2人ゲームの大きな特徴である。それだけに均衡点の意味を理解するにも迷いがない。しかし、表1.18の例を考えればわかるように、非ゼロ和2人ゲームでは、2人のプレイヤーがマクシミン原理にしたがって戦略を選択しても、均衡点にならないこともある。
表1.18 非ゼロ和2人ゲームの均衡点とマクシミン原理
| プレイヤー1の戦略 | プレイヤー2の戦略 | |
|---|---|---|
| 1 | 2 | |
| 1 | (3, 2) | (4, 4) |
| 2 | (2, 3) | (6, 6) |
| マクシミン原理に則ったプレイヤー1の戦略 | |
| マクシミン原理に則ったプレイヤー2の戦略 |
非ゼロ和2人ゲームでは、なぜこうしたことが起きてしまうのだろうか。囚人のジレンマにせよ、両性の闘いにせよ、それが生じるのは非ゼロ和だからである。実は、なぜ非ゼロ和なのかということが大問題なのである。非ゼロ和ゲームを考えることは、ゼロ和ゲームの単なる拡張ではなく、ゲームの本質が根本的に変質してしまうことを意味しているようだ。簡単に言えば、非ゼロ和2人ゲームとはゼロ和3人ゲームの第3のプレイヤーがゲームの構造上現れていないゲームであると考えられる。von Neumann & Morgenstern (1944, ch.11)ではこれを架空のプレイヤー(fictitious player)と呼んだが、この第3のプレイヤーの特性がこのゲームにとっては決定的に重要である。こうしたことから、これ以降、本書では、純正2人ゲームであるゼロ和2人ゲームについてのみ考えることにする。
第1章では2人ゲーム、特にゼロ和2人ゲームを中心に考えてきた。実は、個人の決定問題(decision problem)は、ゼロ和2人ゲームとして定式化することができる。いま、プレイヤー1、2がそれぞれ
という設定のゼロ和2人ゲームを考えてみよう。
まず、プレイヤー1である意思決定者の戦略を行動(action)と呼び、意思決定者のとりうる行動の集合を
A={a1, a2, ..., am}
で表す。一方、プレイヤー2である自然の戦略を自然の状態(state of nature)と呼び、自然のとりうる状態の集合を
Ω={θ1, θ2, .., θn}
で表す。そして、真の自然の状態(true state of nature)が θj のとき、意思決定者が行動aiをとることによって得られる意思決定者の利得を
v=V(ai, θj)
で表すことにしよう。もちろんゼロ和ゲームであるから、この意思決定者の利得にマイナスをつけたものが、自然の利得になるわけである。利得は、とりあえず金額を表していると考えてもらいたい。こうして、意思決定者の行動と自然の状態の組み合せによって決まる意思決定者の利得は、表2.1のような決定表(decision table)と呼ばれる利得表によって表される。決定理論では、このように定式化された意思決定者対自然のゼロ和2人ゲームで、自然または環境に対峙した意思決定者の決定問題が扱われる。
表2.1 決定表
| 行動 | 自然の状態 | |||
|---|---|---|---|---|
| θ1 | θ2 | …… | θn | |
| a1 | v11 | v12 | …… | v1n |
| a2 | v21 | v22 | …… | v2n |
| : : | : : | : : | : : | |
| am | vm1 | vm2 | …… | vmn |
ところで、プレイヤー2を自然や環境と考えるのは、後ほどプレイヤー1がプレイヤー2の出す手に関して情報収集するケースを考える際に、プレイヤー2が通常の人間のように、それに対する防護策を講じたり、対抗策をちらつかせたりすることがないことを正当化するための設定である。自然や環境は泰然として大きい存在なのである。より正確にいえば、環境は制御不能な要因(uncontrollable factors)の集合であると定義される。したがって、定義通りなら、環境は制御することができない。つまり環境は意思決定者から影響を受けないわけである。しかし、環境自身が自律的に変化していくこと(Takahashi, 1987, ch.4)や意思決定者が環境を「住み替える」ことまで否定しているわけではない。こうした環境の定義を受け入れたとしても、環境が意思決定者にとって固定されたものであることを必ずしも意味していないのである。これは例えば、意思決定者が対戦相手である環境を、状況を見ながらやり過ごすこと(やり過ごしについては第7章を参照のこと)も許容しうる定義なのである。
しかし、このようにしてプレイヤー2を制御不能な自然と見ることで、この自然に対しては、どの程度制御できるかではなく、どの程度知ることができるかが重要になってくる。こうして、自然がどの状態をとるのかについての意思決定者の知識のレベルとして、次のような「不確実性」のレベルを考えることになる(cf. Luce & Raiffa, 1957, p.13; March & Simon, 1958, p.137 邦訳pp.208-209)。
こうした事態がさらに進んで、自然の状態の集合 Ω も知らず、各行動によって引き起こされる可能な結果の集合についても定かではないケースも考えられる。こうしたケースは、あいまい性(ambiguity)と呼ばれ、ここで扱われる決定理論系の決定問題とは別の枠組みで議論される(第7章を参照のこと)ので、ここではこの 1~3 の三つのケースを考えることにしよう。第1章のゼロ和2人ゲームの理論では、両プレイヤーが厳密な不確実性のケースに直面していたことになる。決定理論では、プレイヤー1に確実性のケースやリスクのケースを許すことで、新たな展開が考えられるのである。
このうち、1の確実性下の意思決定(decision under certainty)については、確実性下では真の自然の状態がわかっているので、n=1 を仮定しているのと同じことになる。いま真の自然の状態を θt とすると、決定表の該当する θt の列だけを抜き出した決定表を考え、利得を最大にする行動を選べばよい。
もっとも、この確実性のケースは、2のリスクのケースの特別な場合でもある。もしリスクのケースである自然の状態 θt の生起する確率が1、他の自然の状態の生起する確率が0であるとき、つまり、
(p(θ1), ..., p(θt-1), p(θt), p(θt+1), ..., p(θn))=(0, ..., 0, 1, 0, ..., 0)
のとき、リスクのケースは確実性のケースと同じことになる。そこで問題は、2のリスクをともなう意思決定(decision with risk)である。ゼロ和2人ゲームが、勝った方が取るという約束で勝負事に金品を出すという意味での「かけ(賭)ゲーム」を扱っていたのに対して、リスクをともなう意思決定では「くじ(籤)」を扱うことになる。くじとは、紙片、竹片、こよりなどに文句または符号を記しておき、その一つを抜き取らせ、吉凶、勝敗、等級などを決定する、あのくじである。この章ではこのリスクをともなう意思決定について考えてみよう。後述するように、このリスクのケースでは期待効用原理に則って意思決定を行なえば良い。
また、3の厳密な不確実性下の意思決定(decision under strict uncertainty)は第1章のゼロ和2人ゲームの理論で既に考察済みである。多様な意思決定原理が考えられるものの、ゼロ和2人ゲームの均衡点が存在するとき、それを達成するのは、2人のプレイヤーがワルドのマクシミン原理に則って意思決定を行った場合だけだということは、既に第1章で明らかにされている。この章では、リスクのケースで生み出された期待効用の概念を使って、この確実性のケースでもさらに一般化をはかり、均衡点が常に存在すること、それがやはりマクシミン原理に則った意思決定によってもたらされるということを明らかにする。
リスクをともなう意思決定では、意思決定者は Ω 上の確率分布 (p(θ1), p(θ2), ..., p(θn)) を知っているので、 一つの考え方としては、確率を使って、これから述べるような期待金額を計算してみて、それをもとにして選択を考えるという方法がある。
いま見分けのつかない、箸ほどの大きさの木の棒を2本用意し、その先端部分に、「当り」、「はずれ」と各々1本ずつ書き、その先端の文字部分を見えないように壷状の容器に入れておき、2本の棒のうちから1本を引くというくじを考えてみよう。このくじ引きの道具を使って、例えば次のような異なった賞金パターンをもつ2種類のくじを考えることができる。
A1もA2も金額の大きさはともかくとして、商店街の歳末福引抽選などでよくある賞金パターンであろう。これを決定表の形で表すと、表2.2のようになる。くじA1とくじA2のどちらかを選んでもよいといわれたときに、あなたはどちらのくじを選ぶだろうか。
表2.2 くじの決定表
| くじ | 自然の状態 | |
|---|---|---|
| θ1: 当り | θ2: はずれ | |
| A1 | 1000円 | 0円 |
| A2 | 200円 | 100円 |
理想的な木の棒、壷であれば、「当り」の出る確率と「はずれ」の出る確率は等しいはずなので、共に1/2と考えてよいだろう。したがって、
p(θ1)=p(θ2)=1/2
この確率を使うと、この2種類のくじ A1 とくじ A2 の各々に期待できる金額(=「期待金額」)を計算してやることができる。具体的には、次のように各賞金額にそれが得られるはずの確率をかけてその総和を求めるのである。
くじ A1 の方が期待できる金額が高いので、大多数の人は A1 のくじの方を選択することになるだろう。そして、くじの参加料が500円未満ならば、くじ A1 に参加した方が得で、参加すべきであろうし、くじの参加料が150円未満ならば、くじ A2 に参加することも考えられる。もっとも、そのときでも、くじ A1 の方が期待金額は高いので、くじ A1 の方に参加すべきだろうが……。
今の計算をより一般的に表現してみよう。くじの賞金 X はそれがとる各値 xi に対して、それぞれ確率 p(xi) が与えられている変数であり、これを通常、確率変数(random variable)と呼び、大文字で表す。この確率変数である賞金Xの期待値は次のように定義される。
E(X)=Σi=1m p(xi)・xi
となる。ここで、各々の賞金額 xi は、それが得られる確率 p(xi) によって加重され、より得られやすい賞金額は、より大きい重みをつけられる。このように、確率変数のとりうる値を確率をウェイトとして加重平均して求めた値を期待値(expectation)という。この場合は、賞金額の期待値なので期待金額(expected monetary value)というわけである。
いま、くじを n 回引いたときの賞金額の平均を
Xn=(X1+X2+
・・・+Xn)/n
としたとき、この平均賞金額も確率変数になる。確率論の大定理、大数の弱法則(weak law of large numbers)によると、任意の定数 ε>0について、
P(|Xn-E(X)|>ε)→0, n→∞
がいえる。つまり、くじを n 回引いたときの平均賞金額 Xn は、くじを引く回数 n が十分に大きければ、期待金額 E(X) にいくらでも近い値をとることがきわめて確実なのである。逆に言えば、通常は、くじの期待金額 E(X) は、くじを何万回、何十万回も繰り返して行ったときに得られる金額の平均を表していると考えてよい。
ところで、先ほどの例で、金額の数字の単位が「円」ではなく、「万円」であっても、A1 のくじの方が期待できる金額が高いので、大多数の人は A1 のくじの方を選択することになるだろう・・・・・・といえるだろうか。つまり、
次のようなルールに基づく一種のくじを考えよう。
このくじでは理想的な硬貨を投げるので、1回目に表が出る確率は1/2、2回目に初めて表が出る確率は (1/2)2=1/4、3回目に初めて表が出る確率は (1/2)3=1/8、・・・・・・、n回目に初めて表が出る確率は (1/2)n となる。したがって、このくじから得られる賞金Xの期待値である期待金額は
| E(X)= | (1/2)×2 | + | (1/2)2×22 | + | (1/2)3×23 | + | ・・・・・・ | + | (1/2)n×2n | + | ・・・・・・ |
| = | 1 | + | 1 | + | 1 | + | ・・・・・・ | + | 1 | + | ・・・・・・ |
| = | ∞ |
そこで登場するのが、ダニエル・ベルヌーイ(Daniel Bernoulli)の解決として有名な説明である。簡単に言えば、くじによって金銭そのものを得るのではなく、金銭の効用(utility)を得ていると考えれば良いというものである。そして金額が1単位、例えば1万円増えたときに、これにともなって増加する効用の大きさ(これを限界効用(marginal utility)という)が、金額が大きくなるにしたがって逓減すると考えるのである。これを限界効用逓減の法則(law of diminishing marginal utility)ともいうが、具体的には次のような効用関数を考えてみればわかる。いま金額 x の効用を
u(x)=log10 x
としよう。するとここでは常用対数をとっているので、金額 x が10倍になるごとに効用は1ずつ増えることになる。そこで、このくじから得られる金額の効用の期待値を求めると
E(u(X))=Σi p(xi) u(xi)
=(1/2)×u(2)+(1/2)2×u(22)+(1/2)3×u(23)+・・・・・・+(1/2)n×u(2n)+・・・・・・
=(1/2)×log2+(1/2)2×log22+(1/2)3×log23+・・・・・・+(1/2)n×log2n+・・・・・・
=(log 2){1・(1/2)+2・(1/2)2+3・(1/2)3+・・・・・・+n・(1/2)n+・・・・・・}
=2 log 2=log 4
=u(4)
となる。これを期待効用(expected utility)と呼ぶわけだが、期待金額で考えるのとは違い、この期待効用で考えると、このくじのもたらす効用は、確実に得られるわずか4万円の金銭が与える効用に等しくなってしまうのである。実は上の計算は対数の底が何であっても成立する。したがって、対数関数型の効用関数であれば、対数の底が何であっても、それをもつ人にとっては、このくじのもたらす効用は、確実に得られる4万円の金銭が与える効用に等しい。このように、リスクをともなう資産をリスクのない安全な資産に換算した場合の価値を確実同値額(certainty monetary equivalent)という。
ところで、なぜ効用関数として対数関数が登場したのだろうか。いま、ある個人の富の量が、x から x+h へと増大したとしよう。このとき、この人の効用の増加分は、富の量の増加分 h に比例するが、初期所有量xとは反比例する関係があると考えるのである。そのことを数式で書くと、k をある定数とすると、
u(x+h)-u(x)=k(h/x)
∴ [u(x+h)-u(x)]/h=k/x
したがって、
u'(x)=limh→0 [u(x+h)-u(x)]/h=k/x
この微分方程式を満たす効用関数 u(x) は
u(x)=k log x+C
ここで、k=1/log a, C=0 とおくと、u(x)=log x/log a=loga x という対数関数型効用関数が得られるのである。
もっとも、このように説明ができたからといって、期待金額が無限大になっているというのは計算違いだったわけではない。くじに繰り返して参加できることが許されていて、元手さえ十分にあれば、提示された参加料がいくら高くても(有限の金額のはずだから)くじに参加し続けた方がよいのである。もし、くじ券が多くの人に散らばって所有されているような場合には、「参加し続ける」という表現は「くじ券を買い集める」と言い換えることもできる。対数関数型の効用関数をもつ人にとっては、このくじのもたらす効用は、確実に得られる4万円の金銭が与える効用に等しいわけだから、このようなくじ券をもっている人に4万円以上の金額を提示すれば、くじを売ってくれるはずである。こうしてくじを買い集めていけば、必ずもうかるはずなのである。しかし、何万本もくじを買い集めることができるのだったら、本当に金に糸目をつけずに買い集めてしまってもよいのだろうか。
サンクトペテルブルクのパラドックスは理屈の上では理解できるが、直感的にはもう一つ納得がいかない。本当に期待金額が無限大といえるようなことが期待できるのだろうか。硬貨を次々と投げ続け、最初に表が出るまでの試行回数を N とすると、確率変数 N は1, 2, 3, ...の値をとりうる。表を H (head)、裏を T (tail)とすると、
| 1回目 | 2回目 | ・・・・・・ | n-1回目 | n回目 |
| T | T | ・・・・・・ | T | H |
というように、n-1回表が続き、最後の n 回目に表が出るわけだから、表の出る確率を p、裏の出る確率を 1-p とすると、n 回目に初めて表の出る確率は
f (n)=(1-p)n-1p
となる。これは初項 p、公比 1-p の等比数列つまり幾何数列の形をしているので、幾何分布 (geometric distribution)とよばれる。幾何分布にしたがう確率変数 N の期待値を求めてみると、
E(N)=Σnf (n)=p+2(1-p) p+3(1-p)2p+4(1-p)3p+・・・・・・
また
(1-p)E(N)=(1-p) p+2(1-p)2p+3(1-p)3p+4(1-p)4p+・・・・・・
であるから、
E(N)-(1-p)E(N)=p+(1-p) p+(1-p)2p+(1-p)3p+(1-p)4p+・・・・・・=p/{1-(1-p)}=1
したがって、
E(N)=1/{1-(1-p)}=1/p
つまり、期待金額は無限大かもしれないが、期待回数は E(N)=1/p で有限であり、もし理想的な硬貨で p=1/2 であれば、E(N)=2 にしかならないのである。
これは、回数が増えるにしたがって急速にとりうる確率が低下するためで、確率 f (n) が実際にどのような値をとるのかを計算してみるとすぐにわかる。ウォーミング・アップのつもりで、次のような簡単なBASICのプログラムを作って計算してみよう。
10 'GEOMETRIC DISTRIBUTIONプログラムの中の記号#のついている変数は倍精度型であることを示していて、通常#のついていない単精度変数の有効桁が7桁で、出力のとき7桁目が四捨五入されて6桁以下で表示されるのに対して、#のついた倍精度の変数は、有効桁16桁で、16桁以下で表示される。
このプログラムでは、行番号30にあるように n≦15 までの計算をさせるわけだが、その結果は表2.3のとおりになる。累積確率分布をみると、n が16以上になる確率は、わずかに 0.00003 程度、つまり10万分の3ほどしかない。ちなみに15回続けて裏が出て、16回目に初めて表が出たとき(n=16)の獲得金額は、6億5,536万円という巨額になる。
表2.3 幾何分布
| 回数 n | 確率分布 f (n) | 累積確率分布 F(n)=Σu=1n f (u) |
|---|---|---|
| 1 | 0.5 | 0.5 |
| 2 | 0.25 | 0.75 |
| 3 | 0.125 | 0.875 |
| 4 | 0.0625 | 0.9375 |
| 5 | 0.03125 | 0.96875 |
| 6 | 0.015625 | 0.984375 |
| 7 | 0.0078125 | 0.9921875 |
| 8 | 0.00390625 | 0.99609375 |
| 9 | 0.001953125 | 0.998046875 |
| 10 | 0.0009765625 | 0.9990234375 |
| 11 | 0.00048828125 | 0.99951171875 |
| 12 | 0.000244140625 | 0.999755859375 |
| 13 | 0.0001220703125 | 0.9998779296875 |
| 14 | 0.00006103515625 | 0.99993896484375 |
| 15 | 0.000030517578125 | 0.999969482421875 |
それでは、実際にこのサンクトペテルブルクのパラドックスのくじに挑戦して、一体どのくらいの金額を平均的に獲得できるのか試してみよう。といっても、自分で硬貨をいちいち投げ上げるのではあまりにも大変だ。そこで、パソコンに硬貨投げを代わりにやってもらうことにしよう。それには乱数が用いられる。BASICでは、乱数発生器(random number generator)にあたるのは、関数 RND で、これによって 0 以上 1 未満の乱数が与えられる。ただし、このように機械的に発生される「乱数」は厳密な意味では疑似乱数(pseudo random numbers)とよばれるものである。通常は乱数とみなしてかまわない。
そこで、この硬貨投げのくじを数千本もやれば平均賞金額はべらぼうな額になるのかどうかを見るために、まずは1万本まで、1,000本ごとにくじ1本当りの平均獲得金額を求めるプログラムを組むと、次のようになる。
110 'ST. PETERSBURG'S PARADOXパソコンに硬貨投げをやらせた結果、くじ1本当りの平均賞金額は表2.4(a)のようになる。これによると、4,000本のくじをやったときには、平均約22万円の賞金が得られるが、表2.4(b)によると、くじ1万本を終了した段階でも、硬貨投げが n=15 までいったのは、たったの1回で、n≧16 は一度もなかった。どうも数千本ではまだ無理のようである。もっとくじに挑戦すれば、くじ1本当りの平均賞金額は上昇するのだろうか。そこで、10万回まで、今度は1万回ごとに平均賞金額を求めてみると表2.5のようになり、平均賞金額は上昇するというより、むしろ14万円台に落ちついていく気配がある。この段階でも、まだ n≧16 は一度も経験していない。どうも数万本でもまだ無理らしい。しかし、100万本まで10万本ごとに平均賞金額を求めてみても、結局は表2.6のように15万円を少し超えるぐらいであり、くじ100万本を終了した段階で、15万1,825円であった。対数関数型の効用関数を用いたときの確実同値額である4万円よりは高くなるものの、やはり「もうかる」参加料の水準はせいぜい10万円台かもしれない。
ちなみに、さすがに100万本もやると、n=16 は7回ほど経験している(最初は101,567本目)。しかし、幾何分布の理論値では n≧16 は30回ほど経験していていいはずなので、これと比べるとまだ差があり、この辺が理屈通りにいかない理由かもしれない。とはいうものの、期待金額が無限大になってしまうとはいっても、そのスピードは想像するよりもかなりゆっくりであることには変わりはなく、その意味では、効用の概念を使わなくても、このパラドックスはある程度解決できたともいえそうだ。つまり、100万本もやってこんなもんだということは、平均賞金額が無限大になってしまうなどと想像させるような事態に遭遇することは、日常生活ではまずありそうにない。これぞまさに杞憂というべきだろう。
しかし、第1章の実験1.2をやってみればわかるように、たとえ確率がからんでこなくても、Bernoulliが考えたような効用関数の存在を暗示する現象がわれわれの身の回りに多いのは事実である。
表2.4 1万本のくじのシミュレーション
(a)くじ1本当りの平均獲得金額
| くじの本数 | くじ1本当りの 平均獲得金額 |
|---|---|
| 1,000 | 12.464 |
| 2,000 | 12.334 |
| 3,000 | 14.248 |
| 4,000 | 21.9085 |
| 5,000 | 19.4812 |
| 6,000 | 18.161 |
| 7,000 | 17.312 |
| 8,000 | 17.1215 |
| 9,000 | 17.9193 |
| 10,000 | 17.4808 |
(b)くじの分布
| 初めて表が出る までの回数 | くじの本数 |
|---|---|
| 1 | 4,960 |
| 2 | 2,492 |
| 3 | 1,235 |
| 4 | 665 |
| 5 | 314 |
| 6 | 171 |
| 7 | 92 |
| 8 | 29 |
| 9 | 16 |
| 10 | 14 |
| 11 | 7 |
| 12 | 2 |
| 13 | 2 |
| 14 | 0 |
| 15 | 1 |
表2.5 10万本のくじのシミュレーション
(a)くじ1本当りの平均獲得金額
| くじの本数 | くじ1本当りの 平均獲得金額 |
|---|---|
| 10,000 | 17.4808 |
| 20,000 | 14.8508 |
| 30,000 | 15.1604 |
| 40,000 | 14.8143 |
| 50,000 | 14.3299 |
| 60,000 | 14.8329 |
| 70,000 | 14.5664 |
| 80,000 | 14.6415 |
| 90,000 | 14.5922 |
| 100,000 | 14.5849 |
(b)くじの分布
| 初めて表が出る までの回数 | くじの本数 |
|---|---|
| 1 | 50,002 |
| 2 | 25,007 |
| 3 | 12,629 |
| 4 | 6,181 |
| 5 | 3,061 |
| 6 | 1,545 |
| 7 | 806 |
| 8 | 377 |
| 9 | 189 |
| 10 | 112 |
| 11 | 48 |
| 12 | 26 |
| 13 | 8 |
| 14 | 7 |
| 15 | 2 |
表2.6 100万本のくじのシミュレーション
(a)くじ1本当りの平均獲得金額
| くじの本数 | くじ1本当りの 平均獲得金額 |
|---|---|
| 100,000 | 14.5849 |
| 200,000 | 15.0347 |
| 300,000 | 15.1952 |
| 400,000 | 15.2728 |
| 500,000 | 15.2943 |
| 600,000 | 15.1889 |
| 700,000 | 15.1822 |
| 800,000 | 15.2584 |
| 900,000 | 15.2585 |
| 1,000,000 | 15.1825 |
(b)くじの分布
| 初めて表が出る までの回数 | くじの本数 |
|---|---|
| 1 | 499,330 |
| 2 | 249,862 |
| 3 | 126,527 |
| 4 | 62,057 |
| 5 | 31,009 |
| 6 | 15,612 |
| 7 | 8,010 |
| 8 | 3,725 |
| 9 | 1,870 |
| 10 | 1,045 |
| 11 | 526 |
| 12 | 252 |
| 13 | 77 |
| 14 | 61 |
| 15 | 30 |
| 16 | 7 |
ここでは、Allais (1953)の考えた例を参考にして、表2.7にあるような4種類のくじを比較することで、期待効用について考えてみよう。
表2.7 アレの反例
| 賞金額 | 確率 | ||
|---|---|---|---|
| 選択機会1 | くじA | 100万円 | 1.00 |
| くじB | 500万円 | 0.10 | |
| 100万円 | 0.89 | ||
| 0円 | 0.01 | ||
| 選択機会2 | くじC | 100万円 | 0.11 |
| 0円 | 0.89 | ||
| くじD | 500万円 | 0.10 | |
| 0円 | 0.90 | ||
1、2の選択は各々もっともらしいが、(2.1)式と(2.2)式を比べると不等号は逆向きになっている。言い換えれば、くじ A を選択する人がくじ D を選択してはおかしいのである。このような場合、確率 1 で得られる賞金を過大評価する傾向があると考えられるが、これは確実性重視効果(certainty effect)と呼ばれる。くじ A を選択する人はくじ C を選択し、くじ B を選択する人はくじ D を選択するのが、期待効用の観点からは「合理的」なはずなのである。
もっとも、この選択機会1、2を教室で学生に提示して選択させると、必ずしも、くじ A とくじ D を選択しないところが面白い。何度か授業の際に試みているが、くじ A とくじ D を選択する学生はせいぜい約半数といったところで、残りの学生は何を選択するかまちまちである。その中には「合理的」な選択ももちろん含まれているのだが、学生に選択した理由を聞くとあまり「合理的」とはいえない理由が多く、金額や確率に対する考え方や印象が多様であることを思い知らされる。つまり、いつでも誰でも、そしてどんないい加減な意思決定でも期待効用さえ用いれば必ず説明ができるというわけではない。しかし、人間の意思決定が「合理的」と思われるいくつかの要件を満たして行われるのであれば、そのときその「合理性」を体現するものとして何等かの効用関数のようなものが存在しているはずだと考えるのは自然な発想である。そして、その範囲においては、人間の合理的意思決定は、期待効用で説明することができるはずなのである。そのことが、これから述べる期待効用原理によって明らかにされる。
これから述べる考察は、すべて1個人の選好に基づいてなされる。その個人のことをここでは「あなた」と呼ぶことにしよう。このような選好が、どのような性質をもっているときに、意思決定は合理的に行われるのだろうか。ここでは Luce & Raiffa (1957, ch.2)を参考にして、これから述べる五つの仮定を満たすような選好を考えることにしよう。
いま、獲得する可能性のある賞金の金額、A1, A2, ..., An の集合を A とする。このとき、A 上のくじ(lottery)とは、互いに排反で全てを尽くすような(mutual exclusive and exhaustive)不確実な事象の集合の一つが起こったときに、あなたの受け取る賞金額を決める装置ということが出来る。つまり簡単に言えば、ここでは、よくできたルーレットや硬貨のように、不確実な事象の各々に結びついて、ある既知の確率が存在しているくじを考えようというわけである。(次の第3章で、ルーレット型くじ(roulette lottery)と呼ばれるものである。)
いま賞金 Ai∈A が当る確率を pi とすると、当然、pi≧0, i=1, ..., n で、Σi pi=1 である。このとき、くじは
L=(p1 A1, ..., pn An)
と書くことにする。このようなくじの集合を RL とおくと、
RL={(p1 A1, ..., pn An): Ai∈A, i=1, ..., n, Σi pi=1, pi≧0, i=1, ..., n}
ということになる。このようなくじを単純くじ(simple lottery)とも呼ぶ。いま
(0・A1, ..., 0・Ai-1, 1・Ai, 0・Ai+1, ..., 0・An)
のような単純くじを考えれば、これは賞金 Ai と同じことになるので、A⊂RL。
そこで、RL に属する任意のくじに対して、あなたは次の仮定にあるような二つの条件を満たす選好順序をもっているとする。いま L1 を L2 より選好するか、または無差別のとき、L1  L2 で表すことにすると、
L2 で表すことにすると、
仮定2.1 任意の Li, Lj, Lk∈RL に対して、
(1) (連結律) Li  Lj または Lj
Lj または Lj  Li が成立する(両方を満たしてもよい)。
Li が成立する(両方を満たしてもよい)。
(2) (推移律) Li  Lj かつ Lj
Lj かつ Lj  Lk ならば Li
Lk ならば Li  Lk。
Lk。
このうち(1)の連結律では両方を満たしてもよいので、L1  L2 でかつ L2
L2 でかつ L2  L1 のときこれを L1~L2 で表わし、L1 と L2 とが無差別であるという。A⊂RL であるから、この仮定2.1から、賞金 Ai∈A, i=1, ..., n については順序付けが可能なので、一般性を失うことなく、便宜上、賞金の添字の値は、A1
L1 のときこれを L1~L2 で表わし、L1 と L2 とが無差別であるという。A⊂RL であるから、この仮定2.1から、賞金 Ai∈A, i=1, ..., n については順序付けが可能なので、一般性を失うことなく、便宜上、賞金の添字の値は、A1  A2
A2  ……
…… An という順序につけられているものとする。この A1 と An を使って、次の二つの仮定がおかれる。
An という順序につけられているものとする。この A1 と An を使って、次の二つの仮定がおかれる。
仮定2.2 (連続性(continuity)) 任意の Ai∈A に対して、
Ai~( p A1, 0・A2, ..., 0・An-1, (1-p) An) (2.3)
となる実数 p (0≦p≦1)が存在する。
この(2.3)式は結局 A1 と An しか問題にならず、A2 から An-1 までは確率 0 で無視することになるので、これを便宜上
Ai~( p A1, (1-p) An)
のように表すことにしよう。この記法をさっそく用いると、
仮定2.3 (単調性(monotonicity))
p≧q ⇔ ( p A1, (1-p) An)  ( q A1, (1-q) An)
( q A1, (1-q) An)
次に、単純くじの繰り返しで、単純くじの賞品が別の単純くじのくじ券になっているようなくじ
C=( p1L1, ..., pmLm)
を複合くじ(compound lottery)と呼ぶことにする。たとえば、歳末ジャンボ宝くじを景品にした商店街の歳末福引のようなものである。この複合くじに対して、次の二つの仮定がおかれる。
仮定2.4 (代替性(substitutibility)) 第 i 成分だけが異なり他が同じである任意の二つの複合くじ (..., pi Li, ...) と (..., pi Li', ...) について、Li~Li' ならば、
(..., pi Li, ...) ~ (..., pi Li', ...)
仮定2.5 (複合くじの縮約(reduction of compound lotteries)) 複合くじは通常の確率計算にしたがって求められた、賞金に達する確率のみを考えた単純くじに評価することができる。
( q1(p11 A1, ..., p1n An), ..., qm( pm1 A1, ..., pmn An))
~(( p11q1+・・・+pm1qm) A1, ... , ( p1nq1+・・・+pmnqm) An)
以上の仮定の意味するところを簡単な例を使って説明しておこう。たとえば、賞金500万円と賞金100万円を比較すれば、普通は賞金500万円の方が選好されるだろう。このような選好関係がすべての賞金額のペアについていえるというのが連結律である。また賞金1000万円と賞金500万円を比較して賞金1000万円が選好されるならば、さきほどの選好関係と賞金500万円で連結させると、賞金1000万円が賞金100万円より選好されることになる。これを推移律というが、こうしたことがくじについてもいえるとしたのが仮定2.1である。
さらに、賞金1000万円か賞金100万円のどちらかが必ず当るくじを考えよう。いま表2.8のように、賞金1000万円の当る確率が0.8のくじAと0.5のくじBの2種類のくじがあるとしよう。当然、賞金1000万円の当る確率が高いくじAの方が選好されるだろう。これが仮定2.2である。
表2.8 仮定2.2の例
| 賞金 | 確率 | |
|---|---|---|
| くじA | 1000万円 | 0.8 |
| 100万円 | 0.2 | |
| くじB | 1000万円 | 0.5 |
| 100万円 | 0.5 |
それでは、もう少し一般化して、賞金1000万円の当る確率を p、賞金100万円の当る確率を 1-p としたくじCを考えよう。そして表2.9のように、これと賞金500万円が確実に当るくじDとを比較するのである。もし p=1 ならば、くじCは賞金1000万円が確実に当るので、結局、くじCとくじDの比較は賞金1000万円と賞金500万円の比較になり、当然くじCが選好されることになる。もし p=0 ならば、明らかにくじDが選好される。それでは、くじCとくじDが無差別になるような p が0と1の間にあるはずである。これが仮定2.3である。
表2.9 仮定2.3の例
| 賞金 | 確率 | |
|---|---|---|
| くじC | 1000万円 | p |
| 100万円 | 1-p | |
| くじD | 500万円 | 1 |
仮定2.4と仮定2.5は複合くじに関するもので、仮定2.4は複合くじを構成している単純くじもしくは賞金をそれと無差別な別の単純くじと置き換えることができるという仮定である。仮定2.5は複合くじで各賞金の当る確率を通常の確率計算によって計算できるとしたものである。
ここでは以上の仮定2.1~2.5の五つの仮定を満たすような場合、合理的に効用関数に基づいて意思決定が行なわれることを定理の形で証明しておこう。ただし、仮定には様々なバリエーションがある。von Neumann & Morgenstern (1944)をはじめとして、決定理論系でも Blackwell & Girshick (1954)や Ferguson (1967)などでも、それぞれがやや異なる仮定を設定している。ここでは Luce & Raiffa (1957) を参考にした上で、定理の証明ができるだけ簡単になるような仮定を設定してみた。いずれにせよ、以上のような仮定を満たせば、効用関数の存在することが次の定理2.1によって示されるので、Luce & Raiffa (1957)を参考にしながら証明しておこう。
定理2.1 (効用関数の存在) あなたが仮定2.1~2.5に従うならば、任意の二つのくじ L1, L2∈RL に対して、
U(L1)≧U(L2) ⇔ L1  L2
L2
であるような関数Uが存在する。
《証明》A⊂RL であるから、仮定2.1から、賞金 Ai∈A, i=1, ..., n については順序付けが可能なので、一般性を失うことなく、便宜上、賞金の添字の値は、A1  A2
A2  ・・・
・・・  An という順序につけられているものとする。仮定2.2から、任意の賞金 Ai に対して、
An という順序につけられているものとする。仮定2.2から、任意の賞金 Ai に対して、
Ai~(ui A1, (1-ui) An)
ならしめる実数 ui (0≦ui≦1)が存在する。
いま任意のくじ L1∈RL を L1=( p1 A1, ..., pn An) とすると、仮定2.4を繰り返し用いることで、
L1~( p1(u1 A1, (1-u1) An), ..., pn(un A1, (1-un) An))
さらに、仮定2.5から、
L1~(( p1u1+・・・+pnun) A1, (1-( p1u1+・・・+pnun)) An)
そこで、p=p1u1+・・・+pnun とおくと、
L1~( p A1, (1-p) An)
で 0=p1・0+・・・+pn・0≦p≦p1・1+・・・+pn・1=1 となっている。同様にして、任意のくじ L2∈RL を L2=( q1 A1, ..., qn An) とすると、q=q1u1+・・・+qnun とおくと、
L2~( q A1, (1-q) An)
で 0≦q≦1。したがって、仮定2.3から
L1  L2 ⇔ p≧q
L2 ⇔ p≧q
このとき、U(L1)=p, U(L2)=q とおけば、
L1  L2 ⇔ U(L1)≧U(L2) □
L2 ⇔ U(L1)≧U(L2) □
定理2.1の証明の中で
Ai~(ui A1, (1-ui) An)
となるように選ばれた ui が、賞金 Ai の効用に当ると考えれば、くじ L=( p1 A1, ..., pn An) に対応して与えられた
U(L)=p=p1u1+・・・+pnun=Σi ui pi
は期待効用(expected utility)ということになる。つまり、あなたの RL 上の選好順序は、賞金の効用の期待値の数値上の順序と同じである。
したがって、定理2.1は、あなたが仮定2.1~2.5を満たしているときには、くじの効用は賞金の効用の期待値と等しく置けることを示している。このように定義された効用概念は、一般に、フォン・ノイマン-モルゲンシュテルン効用と呼ばれて、他の効用概念とは区別されている。前者は基数的(cardinal)効用と呼ばれ、後者は序数的(ordinal)効用と呼ばれる。
ところで、この賞金 Ai の効用を、任意の実数 a>0 および b について、
vi=aui+b
と正の線型変換をすることを考えてみよう。この場合でも、任意の L について、
V(L)=p1v1+・・・+pnvn
とすると、
V(L)=p1(au1+b)+・・・+pn(aun+b)
=a( p1u1+・・・+pnun)+b
=aU(L)+b
つまり、明らかに任意の二つのくじ L1, L2∈RL について
V(L1)≧V(L2) ⇔ U(L1)≧U(L2) ⇔ L1  L2
L2
が成立し、V(L) もまた効用関数となる。このことは、ちょうど温度を摂氏で計っても、華氏で計ってもよいように、効用は、測定の単位や原点のとり方に無関係な尺度であることを意味している。
ちなみに、摂氏 C 度と華氏 F 度の間には、F=(9/5)C+32 という一次式で表される関係があり、温度を測定する尺度は、温度計の目盛の付け方の違いしかなく、温度というものは実質的にはただ一つしかないと解釈していい。こうしたことから、効用関数については、「正の線型変換を除いて一意に定まる」という言い方もされる。
定理2.1によって、リスクのケースでの効用が明確に定義され、期待効用を考えることの妥当性が明らかになった。意思決定者が期待効用を最大にするような戦略を選択する原理を期待効用原理(expected utility principle)と呼ぶ。
前の章でゼロ和2人ゲームを考えた際には、利得行列が鞍点をもたなければ、均衡点は存在しなかった。つまり、純戦略だけを考えたのでは、均衡点が存在しないこともあるのである。しかし、これから述べるようなゲームの混合拡大を考えれば、均衡点が必ず存在することが証明される。これによって、(厳密な)不確実性のケースにおける意思決定原理をより一般的に考えることができる。
2人ゲームでは、これまでプレイヤー1、プレイヤー2は、それぞれ戦略の集合 Π1={1, ..., m}、Π2={1, ..., n} の要素の中から一つの戦略を選択することだけを考えてきた。しかし、各プレイヤーがリスクを伴う意思決定を行うことを許せば、
確実性のケースがリスクのケースの特別な場合であったように、純戦略は混合戦略の特別な場合である。つまり、プレイヤー1の純戦略 i∈Π1 は、i 番目の成分が 1 で、他の成分が 0 であるような確率分布 p=(0, ..., 0, 1, 0, ..., 0) で表すことができるし、プレイヤー2の純戦略 j∈Π2 は、j 番目の成分が 1 で、他の成分が 0 であるような確率分布 q=(0, ..., 0, 1, 0, ..., 0) で表すことができる。
そこで、プレイヤー1とプレイヤー2の混合戦略の集合をそれぞれ
S1={ p=( p1, ..., pm): pi≧0, i=1, ..., m, Σpi=1}
S2={ q=(q1, ..., qn): qi≧0, i=1, ..., n, Σqi=1}
とする。
プレイヤー1が p=( p1, ..., pm)、プレイヤー2が q=(q1, ..., qn) の混合戦略をとるとき、プレイヤー1が純戦略 i、プレイヤー2が純戦略 j をとる同時確率は piqj となり、表2.10(a)の同時確率分布表で示される通りになる。また、表2.10(b)の利得表は効用の単位で書かれていて、プレイヤー1の効用とプレイヤー2の効用の間にゼロ和の関係があるとしよう。
表2.10 混合戦略
(a)同時確率分布表
| プレイヤー 1の戦略 | プレイヤー2の戦略 | |||
|---|---|---|---|---|
| 1 | 2 | ・・・ | n | |
| 1 | p1q1 | p1q2 | ・・・ | p1qn |
| 2 | p2q1 | p2q2 | ・・・ | p2qn |
| : | : | : | : | |
| m | pmq1 | pmq2 | ・・・ | pmqn |
(b)プレイヤー1の利得(効用)表
| プレイヤー 1の戦略 | プレイヤー2の戦略 | |||
|---|---|---|---|---|
| 1 | 2 | ・・・ | n | |
| 1 | a11 | a12 | ・・・ | a1n |
| 2 | a21 | a22 | ・・・ | a2n |
| : | : | : | : | |
| m | am1 | am2 | ・・・ | amn |
この同時確率分布と利得の効用とを重ね合わせると、プレイヤー1の期待効用は次のようになる。
| U1( p, q) | =p1q1a11+・・・+p1qna1n | |
| +p2q1a21+・・・+p2qna2n | ||
| : : | ||
| +pmq1am1+・・・+pmqnamn | =Σ(i, j) piqjaij |
混合戦略を考えた2人ゲームの均衡点は、第1章で純戦略のときに考えたのと同様に定義される。すなわち、( p*, q*)∈S1×S2 が
U1( p*, q*)= max p∈S1 U1( p, q*)
U1( p*, q*)= min q∈S2 U1( p*, q)
を満たすとき、( p*, q*) を均衡点あるいはナッシュ均衡点という。
純戦略だけを考えたゼロ和2人ゲームでは、均衡点が存在しないこともあった。しかし、混合戦略を考えたゼロ和2人ゲームでは、少なくとも一つの均衡点が存在するということが証明される。
定理2.2 混合戦略を考えたゼロ和2人ゲームには少なくとも一つ均衡点が存在する。
この定理の証明はここでは省略する。鈴木(1959, ch.7)には、これから述べるミニマックス定理の形で、帰納法を使ったLoomisによる証明、アルゴリズムを使ったDantzigによる証明が紹介されている。また実はゼロ和、非ゼロ和にかかわらず2人ゲームにはナッシュ均衡点が存在するが、そのことについては、鈴木(1981, ch.3)に、Brouwerの不動点定理を用いたNashによる証明、角谷の不動点定理を用いた角谷による証明が紹介されている。
混合戦略を考えたゼロ和2人ゲームでは、純戦略のときと同様に、2人のプレイヤーがそれぞれマクシミン原理に則って戦略を選択するときに均衡点に達するということが証明できる。いま、純戦略のときと同様に、各プレイヤーはマクシミン原理に則って選択を行い、分がある混合戦略をとったときに、最悪の場合でも得られる期待効用(=保証水準)を考え、この期待効用が最大となるような混合戦略を選択すると考えよう。このときの各プレイヤーの期待効用は、
プレイヤー1: v1=maxp minq U1( p, q)
プレイヤー2: v2=minq maxp U1( p, q)
もちろんゼロ和ゲームなので、プレイヤー2の実際の期待効用はこれにマイナスをつけたものになるわけだが、純戦略のときと同様に、ここではプレイヤー2の期待効用はこの形で表しておくことにする。そうすると、次のミニマックス定理(minimax theorem)が証明される。
定理2.3 (ミニマックス定理) 混合戦略を考えたゼロ和2人ゲームでは、均衡点 ( p*, q*) が存在し、
v1=maxp minq U1( p, q)=U1( p*, q*)=minq maxp U1( p, q)=v2
が成り立つ。
《証明》定理2.2から、均衡点 ( p*, q*) が存在するので、
U1( p*, q*)=maxp U1( p, q*)
U1( p*, q*)=minq U1( p*, q)
したがって、
v1=maxp minq U1( p, q)
≧minq U1( p*, q)
=U1( p*, q*)
=maxp U1( p, q*)
≧minq maxp U1( p, q)=v2
純戦略のときと同様にして、v1≦v2 が証明されるので、
v1=v2 □
つまり、混合戦略を考えたゼロ和2人ゲームでは均衡点が存在し、その均衡点は各プレイヤーがマクシミン原理に則って戦略を選択したときに達成されるのである。決定問題では、この均衡点でのプレイヤー2の戦略、つまり自然がマクシミン原理に則って定めた戦略(Π2 上の確率分布) q* は最悪分布(least favorable distribution)と呼ばれる。
リスクのケースでは意思決定者は Ω 上の確率分布をもとにして期待効用を求め、それを最大にする戦略(純戦略)を選択すれば良い。(この場合、混合戦略を考えずに、純戦略だけを考えていて良い。詳しくは第5章の定理5.4の補題を参照のこと。) しかし、不確実性のケースでは Ω 上の確率分布を知らないので、マクシミン原理に則って混合戦略を選択することで、はじめて均衡に達する。そのとき自然がマクシミン原理に則ってとる混合戦略が最悪分布なのである。
これまで特に断らずに確率という用語を用いてきたが、確率(probability)には少なくとも次の二つの確率があるといわれている。
しかし、このように定義された確率をよく考えてみると、別に実験だの経験的測定だのにこだわったものではないことがわかる。確率の元来の意味は、もっともらしさ (plausibility)とおおよそ同意語なのである。その意味での確率は広義の論理(logic)に属するものである。そして、論理に属するならば、繰り返し実験が不可能なものに対しても確率を考えてもよいはずだ。実際、たとえば人間は競馬をやる際に、まるでレースの結果に対して確率を付与し、期待効用を最大化しようとするがごとく行動するではないか。つまり、経験確率の範疇ではないのだが、競馬で特定の馬が1着になる確率のように、実験や試行のできない再現性のない結果についても確率は考えられるはずである。そして実際に、われわれはそうやってきている。このような確率が主観確率と呼ばれる確率なのである。
そこでさっそく次のような実験から始めてみることにしよう。
実験3.1 手持ちの硬貨の中から、出来るだけ曲ったり、欠けたりしていない均整のとれた硬貨1枚を捜し出して、その硬貨を続けて100回投げて、表が出るか裏が出るかを観察して、その結果を表3.1に記録してみよう。その結果、表の出る相対度数が1/2に近くなっていることを確認してみよう。
表3.1 硬貨投げの実験結果
| 結果 | 度数 | 相対度数 |
|---|---|---|
| 表 | ||
| 裏 | ||
| 計 | 100 | 100% |
ばかばかしいと思うかもしれないが、この機会にとにかく一度は自分の手で硬貨投げを実際に実験してみることを勧める。硬貨投げの実験を自分で一度も経験せずに、経験確率を議論するなど論外である。実際にやってみればすぐにわかることだが、手のひらにのせた硬貨をただそのまま上に20~30cm投げ上げて、手のひらで受けるだけでは、表なら表、裏なら裏とほとんど同じ面が続けて出てしまい、「不確実」な結果は生まれてこない。納得のいくほどランダムにするには何らかの工夫が必要である。各自工夫してみよ。
ところで、自分で行なった実験結果から、表の出る確率が1/2であるということに納得がいったであろうか。この場合、可能な限り理想的な硬貨を使って実験したはずであるから、表の出る相対度数が1/2に近くなることはある程度予想されたことである。したがって、この硬貨の表の出る確率 p を1/2に等しいとおくのは、一つの近似の方法ではある。しかし、良く考えてみると、出来るだけ理想的な硬貨を選んだといっても、硬貨の表の図柄と裏の図柄は異なっているし、ごくわずかではあっても、表が出やすい、あるいは裏が出やすいという「かたより」(bias)が存在しているはずである。表の出る確率 p を1/2とおいてしまうことは乱暴すぎるかもしれない。そこで、この実験結果から得られた表の出る相対度数を p に等しいとおくことがもう一つの近似の方法である。いずれにせよ、こうして実際に実験や試行を行い、その結果として得られたものが経験確率である。
p を1/2に等しいとおくか、それとも実験で得られた相対度数と等しいとおくかは些細な問題に思えるかもしれない。それでは、この瞬間、あなたの住む都道府県で次に生まれる赤ちゃんの性別が男か女かを予測することを考えてみよう。「次に生まれる赤ちゃんの性別」は不確実な事象で、先ほどの硬貨投げと同様に、男女どちらかが多めに生まれるという理由はなさそうだし、男が生まれることも女が生まれることも同様に確からしいので、男の生まれる確率 q は1/2に近似してもよいと思われるかもしれない。
ところが、硬貨を投げる実験を行って、表の出る相対度数を調べたように、長期的に記録を調べて男の出生する相対度数を「科学的」に調査してみると、実は、出生時における男児と女児の比、より専門的には、女児を100としたときの男児の比のことを出生性比というが、この出生性比がほぼ105でおおむね安定しているという事実がわかっている。このことは統計上よく知られた事実で、日本でも明治以来、年間出生性比はほとんどの年で104から106の間にあることがわかっている。出生性比が105だとすると、男児の相対度数は 105/(105+100)≒0.512 となり、1/2つまり50%とはわずか1.2%ながらも開きのあることになる。この科学的な調査結果をふまえてもなお、q を0.5に等しいとおくか、それとも調査で得られた相対度数0.512と等しいとおくかは些細な問題だと言い切れるだろうか。
先ほどの硬貨投げは、わずか100回しか投げなかったのだから、出生比率とは事実としての重みが違うと思われるかもしれない。そこで次のような簡単なBASICのプログラムを組んでパソコンに「硬貨投げ」を何万回もやらせてみることにした。表(head)の回数をH、裏 (tail)の回数をTで表すことにすると、次のようなプログラムになる。
100 'COIN TOSSING第2章でも述べたように、BASICでは、乱数発生器(random number generator)にあたる関数 RND で、0以上1未満の一様乱数が与えられる(行番号130の行)。このプログラムを実行させた結果、まず最初の1万回まで1,000回ごとに表の出た回数と相対度数を拾い上げてみると、表3.2(a)のようになる。最初の1,000回では相対頻度は1/2以下だったが、2,000回以降では一貫して、相対頻度は50.5%以上である。シミュレーションの最中、この動きを見ていて、このプログラムの中の乱数発生の関数 RND が良い乱数発生器にはなっていないのではないか、あるいは、その使用方法に問題があったのではないかという疑念が頭をもたげてきたのを覚えている。つまり、表の出る確率は p=0.5 ではなく、p=0.508 くらいの設定になっているのではないかと思えたのである。さきほどの出生性比のことを考えると、疑念が生じるのもおわかりいただけよう。つまり、数千回のオーダーでは、とても p=0.5 に近似してしまう決心がつかなかったのである。
それでも辛抱して10万回まで待っていると、今度は1万回ごとに拾い上げた表の出た回数と相対度数は表3.2(b)のようになる。まだ、一貫して p>0.5 ではあるが、さすがに10万回も硬貨投げをすると、めでたく p=0.5 に収束しそうである。ここに至って、ようやくこの「硬貨」の表の出る確率を1/2に近似してもよいという確信がわいてくる。というより、変な話ではあるが、プログラムも乱数発生の関数も間違っていなかったという確信がようやく湧いてくるのである。一応、念のため、さらに10万回ごとに100万回まで見てみると、表3.2(c)のようになり、20万回目を除いて、小数点以下3桁までならば相対頻度は0.500になる。
表3.2 硬貨投げのシミュレーション
(a) 1万回まで
| 試行回数 | 表の出た回数 | 相対頻度 |
|---|---|---|
| 1,000 | 497 | 0.497 |
| 2,000 | 1,012 | 0.506 |
| 3,000 | 1,538 | 0.513 |
| 4,000 | 2,045 | 0.511 |
| 5,000 | 2,526 | 0.505 |
| 6,000 | 3,035 | 0.506 |
| 7,000 | 3,543 | 0.506 |
| 8,000 | 4,062 | 0.508 |
| 9,000 | 4,581 | 0.509 |
| 10,000 | 5,080 | 0.508 |
(b)10万回まで
| 試行回数 | 表の出た回数 | 相対頻度 |
|---|---|---|
| 10,000 | 5,080 | 0.508 |
| 20,000 | 10,101 | 0.505 |
| 30,000 | 15,117 | 0.504 |
| 40,000 | 20.132 | 0.503 |
| 50,000 | 25,126 | 0.503 |
| 60,000 | 30,219 | 0.504 |
| 70,000 | 35,202 | 0.503 |
| 80,000 | 40,220 | 0.503 |
| 90,000 | 45,102 | 0.501 |
| 100,000 | 50,041 | 0.500 |
(c)100万回まで
| 試行回数 | 表の出た回数 | 相対頻度 |
|---|---|---|
| 100,000 | 50,041 | 0.500 |
| 200,000 | 99,889 | 0.499 |
| 300,000 | 150,128 | 0.500 |
| 400,000 | 200,072 | 0.500 |
| 500,000 | 249,994 | 0.500 |
| 600,000 | 300,182 | 0.500 |
| 700,000 | 350,029 | 0.500 |
| 800,000 | 400,127 | 0.500 |
| 900,000 | 450,169 | 0.500 |
| 1,000,000 | 499,956 | 0.500 |
それでは、最初の1万回のときに、このプログラムの中の乱数発生関数RNDの使用方法に問題があり、表の出る確率は p=0.5 ではなく、p=0.508 くらいの設定になっているのではないかと思えたのは、単なる気の迷いだったのだろうか。その時点で、もし私がプログラムの実行をストップさせ、プログラムを組み直してしまっていたら、どういう結論になっていたのだろうか。10万回まで待てなかったのを責められるだろうか。パソコンでも100万回「硬貨投げ」を行うには1時間ほどかかる。もし本当に硬貨投げをやっていたら、1回硬貨を投げ、結果を記録するのに私なら2秒ほどかかる(実験3.1を実際にやってみると、私は100回投げるのに3分少々を要した)。仮に1回当たり2秒として、硬貨投げをする人を交替させるなどして、とにかく同一の硬貨を使って、休みなしに硬貨を投げ続け、1分に30回、1時間で1800回、1万回硬貨を投げ続けると5時間半は要する。10万回では55.6時間、2日半はかかってしまう。100万回では555.6時間、実に24日目になってようやく100万回に達するのである。
乱数発生関数を使って、p=0.5 と意図的に設定して行っている場合ですら、途中で「気の迷い」の生じるのが人間である。p=0.5 が本当かどうかもわからないまま硬貨を5~6時間投げ続けた結果、p=0.508 であると結論を下してしまうことを責めることができるだろうか。たまたま、表の出る相対度数が1/2からあまりずれていなければ、表の出る確率を1/2と近似してしまう際に、われわれが経験確率と主観確率の差異に思いをめぐらすことはほとんどないであろう。
しかし、出生性比にしても、都道府県単位で毎年の統計を出せば、ほとんどの県では新生児は10万人もいないであろう。一方を「気の迷い」と片付け、他方を「科学的事実」と納得する根拠は、一体どこにあるのだろうか。少なくともそれは、もはや事実やデータの問題ではない。われわれには、それは広義の論理に属するとしか言いようがないのである。
そして実際に、この実験3.1で回数制限をなくして、本人が確信をもつまでという条件に変えて学生にやらせてみると(これは後で実験3.2として登場する)、ほとんど全員が数百回で硬貨を投げるのをやめてしまう。シミュレーションの結果を考えると数十万回の硬貨投げをやらなくてはいけなかったはずなのにである。実は彼らは、表の出る相対度数が1/2に近づいたところで、切りのいい回数で実験を打ち切っていた。つまり、相対度数がどのくらいになるのかを調べるために実験をしたのではなく、相対度数が1/2になるように実験をしたのである。このとき1/2は経験確率だが、同時にもともと主観確率でもあったことになる(3.2cを見よ)。
経験確率では、実際に実験や試行を行い、その結果として得られた相対度数をもとにして、近似的に確率にアプローチすることが特徴となっている。しかし、可能な限り理想的な硬貨を使って実験したときでさえ、表の出る相対度数が1/2からどの程度の範囲に収まっていれば、確率 p を1/2に等しいと近似してよいのかということについては議論してこなかったし、おそらく、議論することは無意味だと思われる。なぜなら、理想的な硬貨を投げて表の出る確率が1/2であると述べるとき、この言明には純粋に演繹的な推論によって、論理の中で到達しているのである。実際に硬貨が投げられることも、それが手元にあることすらも必要ではない。このように確率が広義の論理に属するものならば、それはどのような論理なのだろうか。そのことが次の第3節で明らかにされる。
経験確率と主観確率を整合的に結び付ける方法はないのだろうか。そこでここでは、Anscombe & Aumann (1963)に基づいて、経験確率の言葉で、個人の主観確率を定義することにしよう。第2章で期待効用原理を扱った際に、経験確率に関しておかれた効用理論の仮定、仮定2.1~2.5に、もっともらしい仮定を三つだけ付け加えることで、主観確率の存在を証明することができる。そして、主観確率の単純で自然な定義をすることができる。
これから述べる考察は、すべて1個人の選好に基づいてなされる。その個人のことをここでは「あなた」と呼ぶことにしよう。いま A を賞金額の集合とすると、A 上のくじ (lottery)とは、互いに排反で全てを尽くすような不確実な事象の集合の一つが起こったときに、あなたの受け取る賞金額を決める装置ということが出来る。ここまでは第2章と同じである。違うのはここからで、次の2種類の単純くじ(simple lottery)を考える。
そして、これらの単純くじの繰り返しで、その賞品が別の単純くじのくじ券になっているような複合くじ(compound lottery)を考えるのである。第2章で扱った効用理論は、1のルーレット型くじのみから作られる複合くじ間の比較から構成されたが、これから扱う競馬型くじの主観確率は、ルーレット型くじと競馬型くじとから作られる複合くじ間の比較から構成されることになる。
いま Ai を賞金またはくじ券とし、その Ai が当る経験確率を pi とする。当然、Σi pi=1。このようなルーレット型くじの集合を第2章と同様に RL とおく、
RL={( p1A1, ..., pn An): Ai∈A, i=1, ..., n, Σi pi=1, pi≧0, i=1, ..., n}
ルーレット型くじについては、第2章で既に証明したように、あなたが効用理論の五つの仮定、仮定2.1~2.5を満たすようなRL上の選好順序をもっていれば、RL 上に次のような効用関数を定義することができる。
これは、ルーレット型くじと競馬型くじの複合くじのことである。競馬がs個の互いに排反で全てを尽くすような結果 h1, ..., hs をもつと仮定する。いま、競馬の結果が hi ならばルーレット型くじのくじ券 Ri∈RL が賞品として当るような複合くじを
[R1, ..., Rs]
とする。これが競馬型複合くじであり、その集合を HL とする。
HL={[R1, ..., Rs]: Ri∈RL, i=1, ..., s}
この複合型競馬くじ [R1, ..., Rs] にもルーレット型くじ ( p1 A1, ..., pnAn) の経験確率 p1, ..., pn に相当するものが存在することをこれから証明したいのである。
そこで、今度はあなたが
RL*={( p1[R11, ..., Rs1], ..., pn[R1n, ..., Rsn]): [R1i, ..., Rsi]∈HL, i=1, ..., n, Σi pi=1, pi≧0, i=1, ..., n}
上の選好順序をもっており、効用理論の仮定2.1~2.5を満たしていると仮定しよう。また選好に関しては、[R1i, ..., Rsi] は
(0[R11, ..., Rs1], ..., 0[R1i-1, ..., Rsi-1], 1[R1i, ..., Rsi], 0[R1i+1, ..., Rsi+1], ..., 0[R1n, ..., Rsn])
と同等であると考える。これらの選好関係を  *、
*、 *、~*、結果として得られる RL* 上の効用関数を u* で表す。次の三つの仮定によってこの選好関係はルーレット型くじの選好関係と結び付けられるが、いずれも、競馬の結果はルーレットの回り方に影響されないという直観的考えを反映したものである。
*、~*、結果として得られる RL* 上の効用関数を u* で表す。次の三つの仮定によってこの選好関係はルーレット型くじの選好関係と結び付けられるが、いずれも、競馬の結果はルーレットの回り方に影響されないという直観的考えを反映したものである。
仮定3.1 第 i 成分だけが異なり他が同じである任意の二つの競馬型複合くじ [..., Ri, ...]と[..., Ri', ...] について、もし Ri  Ri' ならば、[..., Ri, ...]
Ri' ならば、[..., Ri, ...]  * [..., Ri', ...]。
* [..., Ri', ...]。
仮定3.2 もし R  R' ならば、[R, ..., R]
R' ならば、[R, ..., R]  * [R', ..., R']。
* [R', ..., R']。
仮定3.3 ( p1[R11, ..., Rs1], ..., pn[R1n, ..., Rsn])~*[( p1R11, ..., pn R1n), ..., ( p1Rs1, ..., pn Rsn)]
このうち仮定3.1の性質は単調性(monotonicity)といわれる。仮定3.2はAnscombe & Aumann (1963)では抜けているが、証明には必要なので、Ferguson (1967)にならって仮定に入れている。仮定3.3は、あなたの受け取る賞金が競馬とルーレットの両方によって決るのであれば、競馬のレースの前にルーレットを回すか、後にルーレットを回すのかは問題にならないということを意味しており、複合くじの順序の反転性(reversal of order)といわれる。あなたが、この三つの仮定と第2章の仮定2.1~2.5を満たせば、主観確率が存在するという次の定理が証明できる。
定理3.1 あなたが仮定2.1~2.5を満たすような RL 上の選好順序と RL*上の選好順序をもち、仮定3.1~3.3を満たすならば、任意の [R1, ..., Rs]∈HL に対して、
u*[R1, ..., Rs]=q1u(R1)+・・・+qs u(Rs), Σi qi=1, qi≧0, i=1, ..., s
であるような s 個の数の組 q1, ..., qs が存在する。
《証明》任意の R, R'∈RL について、R~R' ならば、仮定3.1から、任意の H, H'∈HL に対して、H~*H' となるために、u も u* も共に定数となってしまう。これを等しいとおけば、1=q1+・・・+qs となるので、証明は明らかである。
そこで、もっとも望ましい R1*∈RL ともっとも望ましくない R0*∈RL が存在するとしよう。すなわち、R1*  R0*。すると仮定3.2から
R0*。すると仮定3.2から
[R1*, ..., R1*] 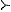 * [R0*, ..., R0*]
* [R0*, ..., R0*]
そこで、
u(R1*)=1 かつ u(R0*)=0 (3.1)
であるように u を選び、
u*[R1*, ..., R1*]=1 かつ u*[R0*, ..., R0*]=0 (3.2)
であるように u* を選ぶ。
ところで、仮定3.1から、もし Ri~Ri', i=1, ..., s ならば
[R1, ..., Rs]~*[R1', ..., Rs']
となる。言い換えれば、u*[R1, ..., Rs] は u(R1), ..., u(Rs) で一意に定まることになる。このことから、これ以後、このような競馬型複合くじを [R1, ..., Rs] の代わりに [u(R1), ..., u(Rs)] で書き表すことにしよう。特に(3.2)式から
u*[1, ..., 1]=1, u*[0, ..., 0]=0 (3.3)
そこでまず、次の補題を証明しておこう。
補題 ある定数 k>0について、0≦ri≦1 かつ 0≦kri≦1, i=1, ..., s ならば
u*[kr1, ..., krs]=ku*[r1, ..., rs]
《証明》
(I) k≦1のとき、RL 上の選好順序は仮定2.1~2.5を満たすので、効用関数が存在し、その性質から、
| [kr1, ..., krs] | ~*[kr1+(1-k)・0, .., krs+(1-k)・0] |
| ~*[(kr1, (1-k)0), ..., (krs, (1-k)0)] |
(II) k>1のとき
u*[r1, ..., rs]=u*[kr1/k, ..., krs/k]
このとき 1/k≦1 なので、これで(I)の結果が使えて、
u*[r1, ..., rs]=(1/k)・u*[kr1, ..., krs]
両辺を k 倍して
ku*[r1, ..., rs]=u*[kr1, ..., krs]
定理の証明に戻る。任意の i について、ri=u(Ri) とすると、(3.1)式から
0≦ri≦1 (3.4)
そこで、c=r1+・・・+rs として、
(I) c=0のとき、(3.4)式から
r1=r2=・・・=rs=0
したがって、任意の q1, ..., qs に対して、
u*[0, ..., 0]=q1u(R1)+・・・+qsu(Rs)=0
(II) c>0のとき、(3.4)式から
ri /c≧0 かつ Σi ri /c=1
したがって、補題から
| u*[r1, ..., rs] | =u*[cr1 /c, ..., crs /c] |
| =cu*[r1 /c, ..., rs /c] |
| u*[r1, ..., rs] | =c{(r1 /c)q1+・・・+(rs /c)qs} |
| =r1q1+・・・+rsqs | |
| =q1u(R1)+・・・+qsu(Rs) □ |
定理3.1によって、仮定3.1~3.3を満たしているときには、競馬型複合くじ [R1, ..., Rs]∈HL に対して、
u*[R1, ..., Rs]=q1u(R1)+・・・+qsu(Rs), Σi qi=1, qi≧0, i=1, ..., s
というように主観確率として機能している q1, ..., qs が存在していることが証明された。この主観確率 qi は定理3.1の証明の中で、第 i 要素だけが1で他の要素は0になっている競馬型複合くじ [0, ..., 0, 1, 0, ..., 0] の効用として定義したものである。
言い換えれば、定理3.1の証明の中で、
u*[r1, ..., rs]=r1q1+・・・+rsqs
となることが示されているので、
u*[1, 0, …, 0]+・・・+u*[0, …, 0, 1]=q1+・・・+qs=1
となり、第三者から見ると、あなたの態度(行動)を説明する際に、第 i 要素だけが1で他の要素は0になっている競馬複合型くじ [0, ..., 0, 1, 0, ..., 0] の効用 u*[0, ..., 0, 1, 0, ..., 0] は確率 qi と同じ機能を果たしていることになる。これは他の競馬型複合くじ [1, 0, ..., 0], ..., [0, ..., 0, 1] との相対的な選択の問題であるから、どれか1頭の馬にだけ張ることができて、しかも馬によって賞金額は変わらないというルールの下で、主観確率 qi は「i 番目の馬が勝ったときにのみ賞金をもらえるが、負けたときには何ももらえないという競馬型複合くじをあなたが選ぶ経験確率」と言い換え、定義することもできる。経験確率が現象に注目したものであるのに対し、主観確率は現象に対するあなたの態度に注目したものなのである。
ところで、もし各結果 hi が既知の経験確率 pi をもっている場合には、競馬型複合くじはルーレット型くじになってしまうので、
[R1, ..., Rs]~*( p1R1, ..., psRs)
したがって、
| [0, ..., 0, 1, 0, ..., 0] | ~*( p10, ..., pi-10, pi1, pi+10, ..., ps0) |
| u[0, ..., 0, 1, 0, ..., 0] | =p1・0+・・・+pi-1・0+pi・1+pi+1・0+・・・+ps・0=pi |
これまでは、主観確率と経験確率の違い、もしくは両者を整合的に定義し、結び付けることを考えてきた。しかし、主観確率に経験的事実としての情報を織り込んでいくという考え方の方がはるかに実際的であろう。そこでここでは、その実際的な方法について考えてみよう。
そのためにはまず、経験確率であれ、主観確率であれ、確率というものは、ある公理を満たしているとする必要がある。いま、ある実験の可能な結果を表す点の集合をその実験の標本空間(sample space)といい、S で表すことにしよう。この標本空間の部分集合は事象 (event)と呼ばれる。
たとえば、実験が10円玉、100円玉各1枚を同時に投げて、おのおのにつき、表、裏のどちらが出たのかを記録するというものだったとしよう。この実験には四つの可能な結果が存在する。すなわち、
S={(H, H ), (H, T ), (T, H ), (T, T )}
ここで H は表(head)、T は裏(tail)を表し、(・,・)の組の最初は10円玉の結果、2番目は100円玉の結果を示している。そして、事象はこの標本空間 S の部分集合であるから、たとえば
Ai={i 枚の表が出る}, i=0, 1, 2
という事象を考えると、
A0={(T, T )}
A1={(H, T ), (T, H )}
A2={(H, H )}
ということになる。
また、関数の定義域の要素として点ではなく、点の集合を考えたものを集合関数(set function)という。以上の道具立てに基づいて、確率の公理(axioms of probability)を簡単な形で示しておこう(Hoel (1971) あるいは Mood et al. (1974) 参照)。
確率の公理 確率測度 P は次の公理を満たす標本空間 S 上で定義された集合関数である。
(1) すべての事象 A について、0≦P(A)≦1
(2) P(S)=1
(3) 互いに排反な事象系列 A1, A2, ... (すなわち Ai∩Aj=φ, i≠j)に対して
P(A1∪A2∪・・・)=P(A1)+P(A2)+・・・
より正確には、これらの公理を満たす集合関数Pを確率測度(probability measure)あるいは確率関数(probability function)と呼ぶのである。この3条件が満たされれば、望ましいとされる他の確率のすべての性質も満たされるということが証明できる。したがって、この確率の公理を満たせば、経験確率、主観確率を問わず、共通の確率の演算が可能になるのである。もちろん事象は集合であるから、通常の集合の演算も可能である。
以上のようなお膳立てが整ったところで、いよいよ主観確率に経験的事実としての情報を織り込んでいく方法について考えてみることにしよう。
事象 B が生起したという条件の下で(ただし、P(B)>0)、事象 A が生起する確率は条件付確率と呼ばれ、
P(A|B)=P(A∩B) /P(B) (3.5)
で定義する。つまり、事象 B が生起している場合、さらに事象 A まで生起する確率である。見方を変えれば、事象 B が生起したという情報が得られたことで、事象 A が生起する確率が変わってくると言うことを意味している。このことをより明確に示しているのが、ベイズの定理である。
いま、A1, A2, ..., An の n 個の事象を考え、A1, A2, ..., An のどれかが必ず生起し、しかも異なる事象 Ai と Aj が同時に生起することはない(=互いに排反)としよう。このことを式で書き表せば、
(1) A1∪A2∪・・・∪An=S
(2) Ai∩Aj=φ, i≠j
ということになる。このような事象 A1, A2, ..., An の集合を標本空間 S の分割(partition)という。
事象 A1, A2, ..., An の生起する確率を P(A1), P(A2), ..., P(An) とすると、
P(A1)+P(A2)+・・・+P(An)=P(S)=1
である。また、新たに事象 B を考えると、分配法則から
| B | =S∩B |
| =(A1∪A2∪・・・∪An)∩B | |
| =(A1∩B)∪(A2∩B)∪・・・∪(An∩B) |
右辺と比べると、左辺では条件の事象が入れ替っていることに注意がいる。いま P(B|A1), ..., P(B|An) が既知であるような事象 B (このような事象 B は情報となりうる)が生起したということがわかれば、事象 Ai の生起する確率は P(Ai) から P(Ai|B) へと変化することになる。つまり、事象 B が生起したという情報が得られたことで、事象 Ai の生起する確率が変わったのである。情報を得る事前か事後かということで分けて、P(Ai) を事前確率 (prior probability)、P(Ai|B) を事後確率(posterior probability)と呼ぶ。
例3.1 いま事象 Ai として、
θ0={表の出る確率が0.50の硬貨}
θ1={表の出る確率が0.51の硬貨}
の二つの自然の状態を考える。事象 B としては、
H={表(head)}, T={裏(tail)}
の2種類を考える。当然のことながら、
P(H|θ0)=0.50, P(T|θ0)=0.50,
P(H|θ1)=0.51, P(T|θ1)=0.49.
となっているはずである。このような P(B|θ) は未知の θ の関数と考えて、尤度関数 (likelihood function)あるいは簡単に尤度(「ゆうど」: likelihood)と呼ばれる。いま、事前確率は主観確率ならばもつことができて、
P(θ0)=p, P(θ1)=1-p
このとき、
w=(P(θ0), P(θ1))=(p, 1-p)
を事前分布(prior distribution)ということもある。
以上のことから、
P(θ0|H)=P(θ0)P(H|θ0)/[P(θ0)P(H|θ0)+P(θ1)P(H|θ1)]=0.5p/[0.5p+0.51(1-p)]
P(θ1|H)=P(θ1)P(H|θ1)/[P(θ0)P(H|θ0)+P(θ1)P(H|θ1)]=0.51(1-p)/[0.5p+0.51(1-p)]
同様にして、
P(θ0|T)=P(θ0)P(T|θ0)/[P(θ0)P(T|θ0)+P(θ1)P(T|θ1)]=0.5p/[0.5p+0.49(1-p)]
P(θ1|T)=P(θ1)P(T|θ1)/[P(θ0)P(T|θ0)+P(θ1)P(T|θ1)]=0.49(1-p)/[0.5p+0.49(1-p)]
このことを図式化してまとめると、図3.1(a)のようになる。ここでは事前分布は特定していないが、たとえば、p=1/2 とすると
P(θ0)=P(θ1)=1/2
すなわち、事前分布は (0.5, 0.5) となり、事後分布は、
H (表)が出ると (0.495, 0.505)
T (裏)が出ると (0.505, 0.495)
というようになる。つまり、情報を得ることで、主観確率は図3.1(b)のように変化することになる。
図3.1 事前確率と事後確率
(a) 事前分布 w=(p, 1-p)

(b) 事前分布 w=(0.5, 0.5)
事象B1の生起する確率が、他の事象B2の生起に影響されないとき、つまり
P(B1)=P(B1|B2)
であるとき、事象 B1 と事象 B2 とは独立(independent)であるという。この式を条件付確率の定義式に代入すると、
P(B1∩B2)=P(B1|B2)P(B2)=P(B1)P(B2)
つまり、二つの事象 B1 と B2 が独立であれば、その積事象 B1∩B2 の確率を二つの事象の確率の積として表すことができる。同様にして、B1 と B2 が独立ならば、
P(B1∩B2|A)=P(B1|A)P(B2|A)
と表すことができる。
この性質を利用すると、繰り返して実験が可能な場合の事前分布、事後分布の動きを簡単に表すことができる。いま2回続けて硬貨を投げるような実験を考えてみると、1回目に生起した事象を B1、2回目に生起した事象を B2 とする。硬貨投げの場合には、B1、B2 とも {H} あるいは {T} のどちらかになる。すると、ベイズの定理から、事前確率 P(Ai) は2回硬貨投げを行なった経験的事実 B1∩B2 の算入によって、事後確率 P(Ai|B1∩B2) になる。
P(Ai|B1∩B2)=P(Ai)P(B1∩B2|Ai)/[Σj P(Aj)P(B1∩B2|Aj)]
ところが、この式の分子は B1 と B2 とが独立であることから
| P(Ai)P(B1∩B2|Ai) | =P(Ai)P(B1|Ai)P(B2|Ai) |
| =P(Ai∩B1)P(B2|Ai) | |
| =P(B1)P(Ai|B1)P(B2|Ai) |
| P(Ai|B1∩B2) | =P(B1)P(Ai|B1)P(B2|Ai)/[ Σj P(B1)P(Aj|B1)P(B2|Aj)] |
| =P(Ai|B1)P(B2|Ai)/[ Σj P(Aj|B1)P(B2|Aj)] (3.7) |
ところで、硬貨投げのような実験はもともと何度も繰り返して実験が可能なわけであるから、以上のような2回続けて行なった硬貨投げの話をt回続けて行なった硬貨投げの話に拡張することができる。いま第1期から第 t 期までの事象の列を B1, B2, ..., Bt で表すことにすると、硬貨投げのように繰り返している各実験の結果が独立であれば、
| P(Ai)P(B1∩B2∩・・・∩Bt|Ai) | =P(Ai)P(B1|Ai)・P(B2|Ai)・・・P(Bt-1|Ai)・P(Bt|Ai) |
| =P(Ai)P(B1∩B2∩・・・∩Bt-1|Ai)・P(Bt|Ai) | |
| =P(Ai∩B1∩B2∩・・・∩Bt-1)・P(Bt|Ai) | |
| =P(B1∩B2∩・・・∩Bt-1)・P(Ai| B1∩B2∩・・・∩Bt-1)・P(Bt|Ai) |
実験3.2 いま例3.1と同様に
θ0={表の出る確率が0.50の硬貨}
θ1={表の出る確率が0.51の硬貨}
の二つの自然の状態を考える。もし θ0 が真の自然の状態のときに、硬貨投げを何回続ければ、表の出る確率が0.50であると「確信」をもつに至るのだろうか。また、θ1 が真の自然の状態のときに、硬貨投げを何回続ければ、表の出る確率が0.51であると「確信」をもつに至るのだろうか。実際に硬貨を投げてやってみよう。
既に述べたように、この実験を学生にやらせてみると、ほとんど全員が数百回でやめてしまう。しかも、そのときには「確信」をもつに至ったというよりも、「もういい」という気持ちになっているようである。しかし、数百回で「確信」に至るとはどうしても思えないので、ここでは不平を言わないパソコンに硬貨投げをさせることにしよう。
もし、θ0 が真の自然の状態のとき、すなわち、使用している硬貨が、表の出る確率0.50の硬貨であったときに、表の出る確率が0.50であるとの「確信」をもつに至る様子を見るために、次のような簡単なBASICのプログラムを組んで、パソコンに硬貨投げをやらせてみることにしよう。
100 'UPDATINGこのプログラムの行番号150、160の2行には、例3.1のところで図3.1(a)に表示された式がそのまま登場していることに注目してほしい。つまり、(3.8)式がいえることから、硬貨投げを何回続けようが、毎期同じ図3.1(a)のプロセスを繰り返すだけでいいのである。第 t-1 期の事後確率を第t期の事前確率とするだけで、あとは毎期ベイズの定理を使って、1期分の更新プロセスを繰り返すだけでよい。これがアップデイティングの強みである。
また行番号120に「P=.5」とあるように、最初の事前確率は w=(0.5, 0.5) から始めることにする。事前確率、事後確率の計算では丸め誤差が累積してくるので、今回は倍精度で計算している(行番号110)。
ここでは既に実験3.1の所で行なった100万回の硬貨投げのシミュレーション結果と対比するために、同じ乱数列を用いてシミュレーションを行なってみた。その結果、まず最初の1万回まで1,000回ごとに事後確率と表の出た相対度数を拾い上げてみると、表3.3(a)のようになる。最初の1,000回では相対頻度は1/2以下で、「表の出る確率が0.50の硬貨である」ことが真である事後確率 p は1/2を超えているが、2,000回以降では、一貫して相対頻度は50.5%以上である。実験3.1の硬貨投げのシミュレーションのときは、この動きを見ていて、このプログラムの中の乱数発生の関数RNDの使用方法に問題があったのではないかと思えたわけだが、実際、「表の出る確率が0.50の硬貨である」ことが真である事後確率 p は2,000回以降一貫して1/2を下回っており、特に9,000回の段階では、p=0.19153 にまで低下している。事後確率の点でも、8割方、今投げている硬貨の表の出る確率は0.51ではないかということになる。
それでも辛抱して10万回まで待っていると、今度は1万回ごとに拾い上げた事後確率と表の出た相対頻度は表3.3(b)のようになる。まだ一貫して相対頻度は0.5以上であるが、さすがに10万回も硬貨投げをすると、事後確率もようやく p=1 に収束しそうであった。一応,念のため、さらに10万回ごとに100万回まで見てみると、表3.3(c)のようになり、一応、小数点以下5桁までならば、事後確率は1.00000になる。したがって、数万回もやって、ようやくこの「硬貨」の表の出る確率は0.51ではなく、0.50であるという確信をもつに至ったということができるだろう。このように事後確率の動きは、実験3.1の硬貨投げのシミュレーションのときの「確信」の動きとよく似ていることがわかる。主観確率のことを確信の度合(degree of belief)と呼ぶこともあるが、まさしく「確信」はベイズの定理によって事後確率を計算した場合の主観確率と同様の軌跡をたどっていたのである。
表3.3 硬貨投げとアップデイティングのシミュレーション
(a) 1万回まで
| 試行回数 | 事後確率 | 相対頻度 |
|---|---|---|
| 1,000 | 0.57934 | 0.497 |
| 2,000 | 0.48001 | 0.506 |
| 3,000 | 0.28494 | 0.513 |
| 4,000 | 0.26893 | 0.511 |
| 5,000 | 0.49002 | 0.505 |
| 6,000 | 0.45018 | 0.506 |
| 7,000 | 0.42069 | 0.506 |
| 8,000 | 0.29318 | 0.508 |
| 9,000 | 0.19153 | 0.509 |
| 10,000 | 0.23147 | 0.508 |
(b) 10万回まで
| 試行回数 | 事後確率 | 相対頻度 |
|---|---|---|
| 10,000 | 0.23147 | 0.508 |
| 20,000 | 0.49007 | 0.505 |
| 30,000 | 0.78928 | 0.504 |
| 40,000 | 0.93825 | 0.503 |
| 50,000 | 0.99304 | 0.503 |
| 60,000 | 0.96236 | 0.504 |
| 70,000 | 0.99733 | 0.503 |
| 80,000 | 0.99926 | 0.503 |
| 90,000 | 1.00000 | 0.501 |
| 100,000 | 1.00000 | 0.500 |
(c) 100万回まで
| 試行回数 | 事後確率 | 相対頻度 |
|---|---|---|
| 100,000 | 1.00000 | 0.500 |
| 200,000 | 1.00000 | 0.499 |
| 300,000 | 1.00000 | 0.500 |
| 400,000 | 1.00000 | 0.500 |
| 500,000 | 1.00000 | 0.500 |
| 600,000 | 1.00000 | 0.500 |
| 700,000 | 1.00000 | 0.500 |
| 800,000 | 1.00000 | 0.500 |
| 900,000 | 1.00000 | 0.500 |
| 1,000,000 | 1.00000 | 0.500 |
以上のようにして、ベイズの定理によってアップデイティングされて得られた事後分布は決定や統計的推論の基礎として用いられることになる。第5章で扱われる逐次決定問題のモデルはその典型例である。このように事後分布を決定や統計的推論の基礎に置く立場をとる人々はベイジアン(Bayesian)と呼ばれる。ベイジアンについては藤本・松原(1976)に詳しい。
これまで決定理論を中心にして、人間の意思決定、正確には個人の意思決定について考えてきた。ところが、人間が一人でポツンと孤立して意思決定している例は存在しない。人間は常に何らかの意味で組織に属して意思決定を行なっている。なぜ人間は組織を作って、その中で意思決定を行なっているのだろうか。これまでの個人の意思決定についての決定理論の議論をふまえた上で、組織について考えてみることにしよう。
組織の構造と機能の基本的特色に大きくかかわっている人間の基本的特性は一般に「限定された合理性」(bounded rationality)という用語で表現される。ここでいう「合理性」とは人間の意思決定に関するものである。これは決定理論の考え方を思い起こすとわかりやすい。つまり、いまいくつかの可能な代替的行動の案があり、そのそれぞれの行動によって引き起こされる結果がわかっていて、それらの結果を評価しうるようなある価値体系があるとしよう。このとき、その価値体系によって、望ましい代替的行動を選択するとき、「合理的」選択と呼ぶのである(Simon, 1976, p.75 邦訳p.96)。
例えば既に扱ったように、決定問題では、意思決定者のとることのできる可能な代替的行動 a1, a2, ..., am があり、それぞれの行動によって引き起こされる結果は、自然の状態 θ1, θ2, ..., θn との組合せ (ai, θj) で決まる。そして、それらの結果を評価するものとして、利得関数 V(ai, θj) が与えられているのである。こうした決定問題の諸要因が与えら れた状況で、どんな意思決定が「合理的」であるとされていたか、前章までの議論を整理 すると次のようになる。
このように、2、3のケースでは、論者によって見解が異なる可能性があると言ってよいだろう。しかも、こうしたさまざまな「合理的」意思決定が、現実のわれわれ人間の意思決定を十分に説明できているものであるかどうかは、かなり疑わしい。例えば、前述のリスクのケースでは、仮に期待利得を最大にする行動を選ぶことが「合理的」であると主張したとしても、サンクトペテルブルクのパラドックスのような状況に直面した場合には、その説得力を失う。それでは、期待効用原理に則って、期待効用を最大にする行動を選ぶことが「合理的」であったと主張しても、アレの反例のような状況に直面した場合には、やはりその説得力を失う。
言い方を変えれば、第2章でも述べたように、そもそも期待効用原理は無限定に、誰にでもいつでも適用可能なものではない。くじの効用関数が存在し、それが賞金の期待効用の形になることは、仮定2.1~仮定2.5の五つの仮定を満たして意思決定が行なわれるときに初めて証明が可能になるものである。また第3章でも述べたように、主観確率も、この五つの仮定に加えてさらに仮定3.1~仮定3.3を満たして、はじめて存在が証明できるものである。これらの仮定を要件として満たしたときに、はじめて一般の意思決定に期待効用原理が適用可能になるのである。個々の仮定は、それぞれ納得のできるものではあるが、これらすべての仮定を常時満たしていることは、われわれ現実の生身の人間にとっては容易なことではない。その意味では、このリスクのケースだけを考えてみても、決定理論においては、現実の生身の人間よりは、かなり条件の整った、言い換えればかなり合理性において優れた「人間」が想定されていると考えなくてはいけない。
こうしたリスクのケースだけに限らず、これまで決定理論や古典的な経済学においては、生身の人間からは乖離したままで、研究者によって比較的自由に「合理的」選択のモデルが作られ、分析が行なわれてきた。したがって、こういった分野で考察される「合理的」選択のモデルは、その前提として、Simon (1976)が「経済人」(economic man)と呼ぶような、全知的に合理的な(omnisciently rational)一種の人間のモデルを想定していると考えざるをえない(Cyert & March, 1963, p.99 邦訳p.144)。
これは決定理論や古典的経済学に共通する本質的な前提である。ここでいう経済人モデルは、より具体的には次のような特徴をもつ人間モデルを指している(Simon, 1976, pp.xxix-xxx 邦文序文p.30; March & Simon, 1958, p.140 邦訳pp.213-214)。
これまでの決定理論の議論から、決定理論では最適基準による選択が行なわれていることは容易に理解できるであろう。ただし、ここで言及されている最適基準の定義は、「すべての代替案」という部分に力点が置かれていると理解されるべきである。つまり正確には、後で触れる満足基準の対照概念にはならない。
しかし、実際の人間はそのような経済人モデルに合致するような行動をとっているのだろうか。例えばいま賃貸の居住用の部屋を探すことを考えてみよう。部屋探しの一つの方法としては、仲介を職業としている不動産業者に出向いて、ファイルされている不動産情報、具体的には間取りとその図面、賃貸条件(賃料、敷金・礼金、管理費等)、物件所在地とその地図・交通手段、築年月、契約期間、入居可能日、設備等を確認して、そのコピーを入手する。それから実際に当該物件まで出かけて、実際に目で見て、交通の便なども足で確かめて、不動産情報の内容を確認することになる。
そこで、議論を簡単にするために、ここでは職場から通勤時間1時間以内の範囲の賃貸の物件に限定して話を進めよう。職場はたいてい交通の便の良い都心部にあるので、政令指定都市クラスの都市圏ならば、通勤時間1時間以内と限定しても、入居者を募集している賃貸のアパート、マンション、一戸建ては、一時点で100件程度にはなるだろう。そのことは住宅関係の情報誌で容易に確認することができる。仮に、住宅関係の情報誌に掲載されているものが、その時点での可能な代替案のすべてだとしよう。(実際にはそれよりもはるかに代替案は多い。また良い物件は情報誌掲載前に各不動産業者の段階で入居者が決まってしまう。) 職場から片道1時間以内の範囲にあるわけだから、職場を基点に行動すると、一つの物件を調べるのに1~2時間はかかると考えるべきであろう。すべての可能な代替案つまり物件を調べるのに、ざっと100~200時間はかかる。1日10時間を部屋探しに投入しても、半月はかかる計算になる。それでもかなり上手に調査スケジュールを組めば、もっと効率的に調べ回ることもできるかもしれない。しかし、よほど暇を持て余している人ならばともかく、この場合のような勤め人にとっては調査効率云々以前の問題で、どだい無理な話である。おそらく数カ月は要する。そして、すべての物件の調査が終った頃には、既にほとんどの物件は入居者が決まってしまっているはずだ。もちろん住宅関係の情報誌だって、その間に何号も最新情報を満載して発行されているのである。ようやく代替案の比較検討に入ろうかという前に、こうした努力は無駄になる。これではいつまでたっても入居できないし、第一、徒労に終ったにもかかわらず、ここまでの物件調査に費やされたコストは、どう低めに見積もっても数十万円に達するだろう。職場から通勤時間1時間以内の範囲に限定してもこの有様である。
こうしたことからも実感できるように、この経済人モデルは現実的ではない。実際、いまの部屋探しの例では、われわれ自身の経験からいって、すべての可能な代替案を考慮しようなどとは最初から考えてもいない。例えば、信頼できるせいぜい2、3の不動産業者からのお勧め物件数件を実際に調べる程度であろう。しかも、各物件についての詳細な知識(つまり居住した場合の結果の知識)は不完全で部分的で、都合の悪いことはあまり教えてもらえないのが普通である。そもそも、物件を探すときには、「職場から通勤時間1時間以内」というような何かポイントになるいくつかの項目だけに関心があり、それについてははっきりした意見をもっているが、その他の項目についての選好はきわめてあいまいなものである。ましてや起こりうる結果のすべてに対しての完全な効用序列などは望むべくもない。
つまり、われわれが部屋探しをするときに直面している「決定問題」は、おそろしく単純で簡単なものなのである。しかも、最適な物件など最初から探そうとも思っていない。極端にいえば、我慢して住んでいられる、あるいはぎりぎり満足できる物件がみつかればいいと思って探しているのである。もちろん、意外な掘出し物がみつかることを期待しているのではあるが……。
こうして自分の行動を振り返ってみればわかるように、少なくても、実際の人間の行動は全知的・客観的合理性に次の3点で遠く及ばないということは容易に指摘しうる(Simon, 1976, p.81 邦訳p.103; March & Simon, 1958, p.138 邦訳p.210)。
実は、われわれが「決定問題」と称しているものも、実際にわれわれが問題を設定し、解くことができるのは、代替案の数がごく限られているか、あるいは、各代替案の結果やその価値、効用が簡単な形をしているものばかりなのである。それは第1~3章を見ればよくわかる。言い換えれば、現実の世界において、経済人モデルが描くように人間が客観的に合理的な行動を選択しているのであれば、実際に人間が扱っているよりもはるかに複雑な問題を定式化し、それを解くことを要求されるはずなのである。しかし、われわれが通常よく取り扱う「決定問題」を考えてみればわかるように、「決定問題」ははるかに単純である。われわれにでも解けるほどに十分に簡単になっているのである。明らかに、実際の人間であるわれわれには、経済人モデルが求めるような高度な問題解決能力は備わっていないし、利用可能な労力や時間にも制約がある。経済人が相手をしている問題のサイズに比べたら、人間の頭脳の能力は、はるかに小さなものにすぎないのである。
そこでSimonが考え出したのが「経営人」(administrative man)の人間モデルである。経営人モデルは、経済人モデルと対比させると、次のような特徴をもっている(Simon, 1976, pp.xxix-xxx 邦訳序文p.30; March & Simon, 1958, p.140 邦訳pp.213-214)。
ここで注意がいるのは、2の満足基準は、暗黙のうちに逐次的な探索過程を前提として考えられているということである。この暗黙の前提に対しては、モデル的により明確にして考察を行なう必要があるので、あらためて§4.3で考えることにしよう(実際には、最適な満足水準を求めることもできるので、ここでのSimonらの満足基準/最適基準の二分法は厳密には正しくない)。
いずれにせよ、以上のようなことから、経営人が合理的に選択を行なうとするならば、経営人が考慮すべき変数のシステムは十分に単純化されていなくてはならない。そのためには、経済人の場合には工夫する必要もなかったなんらかのしかけが当然必要となってくる。例えば、状況定義に他からの重要な間接的影響が及ばないようにすることは、モデルの単純化にはきわめて大切なことであるが、経済人の場合には必要なかったことであり、そのためには、なんらかの意味での望ましい「しかけ」を作ることが必要になってくる。このようなしかけのうち、代表的かつ重要なものとして、組織が登場してくることになる。
ここで考察の基礎となる近代組織論は、Barnard (1938)によって創始され、Simon (1976; 初版1945)や March & Simon (1958)らによって精緻化されたものである。BarnardとSimon、Marchとの間には主張にやや隔たりもあるが、後者を中心にして考えれば、近代組織論は、組織メンバーの限定された合理性が、組織の意思決定過程の中でどのように克服されていくのかということを分析することを基本的テーマとしている。近代組織論はその観点から組織現象を説明するための概念体系と理論的枠組みを確立したといっていいだろう。限定された合理性しかもたない人間が、「合理的」に意思決定をしうるための装置として組織をとらえ、そのために組織がどのような機能を果たしているのかを近代組織論的観点から整理してみよう。
これまでの議論から、限定された合理性を考慮に入れると、経営人たる人間が、たとえなんらかの意味で合理的に意思決定できるとしても、それは人間にとってかなりお膳立ての整えられたような状況下に限られてくることが明らかになった。§4.1.bの合理性の限界についての指摘を逆手にとれば、次のような状況の特性が、意思決定に先立ってあらかじめ定められ、与えられているときにのみ、人間は合理的に意思決定できるにすぎないということがわかる。
つまり決定問題でいうところの、1. 意思決定者の行動の集合、2. 行動によって引き起こされる結果、3. 利得関数、であり、最後の4は、リスクのケースで必要となってくるものである。この四つの状況の特性があらかじめ定められ、与えられているときにのみ、人間は合理的に行動できる。ということは、仮に合理的意思決定者がいるとすると、その合理的意思決定者の状況はこの四つの特性によって、あらかじめ定義されているにちがいないということになる(March & Simon, 1958, pp.150-151 邦訳pp.230-231)。
組織が人間の目的の達成にとって有用な道具であるのは、まさしく個々の人間自体が知識、能力、および時間等について限界を持っているからにほかならない。そのことを克服して、人間にも合理的な意思決定を可能にするために、人間が身を置く状況の方に工夫をして、1~4の四つに代表される状況の特性が、人間になんらかの形で与えられ、定義されるようにするのである。このとき、経営人たる人間に、はじめて合理的意思決定が可能になるのである。したがって、「組織」とは、意思決定に際して考慮すべき変数のシステムがより閉鎖的(=できるだけ重要な間接的影響が存在しない)でかつ単純となるように組織内の人間の意思決定状況を定義し形成する装置だと考えてもよいはずである。
March & Simon (1958, pp.139-140 邦訳pp.211-213)はこうした認識から、次の二つの基本的性格を組み込んだ「合理的選択の理論」(the theory of rational choice)を示した。
したがって、この理論では、人間が組織の中に身を置くことによって、組織の中での心理学的・社会学的過程による濾過作用を受けることを肯定的に扱っていることになる。つまり、組織は、その中に身を置く人間の状況定義の形成過程:

において、現実の状況にふるいをかけ、歪みを加えながら単純化を行うという機能を果たす点でまさに重要なのであり(March & Simon, 1958, pp.154-155 邦訳p.236)、この状況定義の形成過程を経ることで、合理性に限界のある人間が、はじめて合理的に意思決定できるような状況が生まれるのである。そして、組織の他のメンバーについても、同様の過程を経て、合理的意思決定を期待できる。そのことで、さらに当該メンバーの状況定義は単純化が可能になるのである。
March & Simonの「合理的選択の理論」が提示するように、状況定義の諸要素を所与とはせず、それ自体を組織の中での心理学的・社会学的過程といった濾過過程の結果であるとするならば、当然、状況定義の形成過程それ自体が考察の対象となりうる。このような観点からすると、人間の選択について、全体として長々とした過程の最後の瞬間の「決定」にだけ注意を向けるのではなく、それに先行する探索、分析等を含めた複雑な過程の全体に注意を向けることが必要となってくる(cf. Simon, 1977, p.40 邦訳p.54)。
こうした理由から、近代組織論では、組織の分析・考察に当っては、分析の最小単位を意思決定(decision)にではなく、そこに至るまでに登場する意思決定前提(premise)に置くことになる。こうすることで、意思決定を「諸前提から結論を引き出す過程」(Simon, 1976, p.xii 邦訳序文p.8)として扱うことができるようになるのである。こうして、近代組織論では状況定義を所与として片付けてしまわずに、組織の中で、状況定義がどのように形成されてくるのかということ自体に重大な関心を払うのである。
例えば、Simon (1976, pp.xviii-xix 邦訳序文p.17)は、販売部長、生産計画部長、工場長、製品デザイン担当技師の4人の架空の会話を設定すると、
などと予想することは容易であるという。なぜなら、彼らは特定の組織的ポジションにあり、特定の種類のコミュニケーションを受け、特定の部門目標に責任をもち、かつ特定の種類の圧力を経験しているからである。つまり、それぞれがある特定の状況定義に基づいて意思決定を行なっている。したがって、さまざまな組織の中で、さまざまなパーソナリティーをもった人がそれぞれのポストについていながら、その状況定義についてはある程度特定が可能なので、彼らの行動を大まかに予測することはある程度可能なのである。
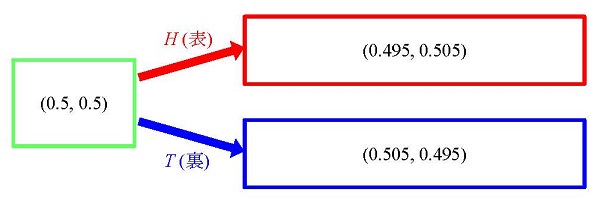
それでは、組織の中で、どのようにして状況定義が形成されてくるのだろうか。いま、図4.1で表されるような個人(とりあえず「Aさん」と呼ぶ)の意思決定の連鎖を考えてみよう。Aさん個人の意思決定過程は、通常それ自体がさらにAさん自身によるいくつかのより細かな意思決定の連鎖として表現される。この図の場合は、ごく単純に、xという意思決定前提がAさんにもたらされたことにより、Aさんの意思決定の連鎖がスタートすると考える。そして、例えば、上側のパスでは満足の諸基準が設定され、下側のパスでは具体的に代替案が探索される。こうして得られた満足の諸基準と代替案を意思決定前提として、意思決定の連鎖の最後の意思決定が行われ、a という行動がとられる。
図4.1 個人(Aさん)の意思決定の連鎖
いま仮に、この意思決定が、前述の部屋探しに関するものだったとしよう。もしAさんがなんらかの組織に属し、図の太枠のなかの意思決定の連鎖である代替案の探索をAさんが自分自身で行わず、その組織の中の他のメンバーであるBさん(例えば人事部厚生課で住居の手配を担当しているベテラン)にやってもらうことにする。つまり、Aさんは自分の意思定過程の一部を組織(実際には組織を構成するメンバーであるBさん)に委譲してしまうわけである。こうすることの利点は、Aさんの意思決定に要する労力・能力・時間を節約することができるということである。実際、有望な代替案探しを同じ会社の信頼できるベテラン担当者にやってもらえば、親身になって良い物件を探してくれるはずである。このような意思決定過程の分業により、Aさんの意思決定過程はかなり単純化されることになる。言い換えれば、Aさんが意思決定に際して直面しなくてはいけないはずだった状況が、組織とかかわりをもつことによって、より単純に定義されることになるのである。
しかし、その反面、Aさんの意思決定の基礎となっている諸前提が組織の他のメンバーからもたらされるために、この場合には、そのメンバーであるBさんの影響に従うことにもなるのである。いま組織の階層構造を考えてみよう。その最下層には、実際に物理的な仕事を行う現業員とよばれる人々がいて、その上の階層には、非現業員である管理者が存在していると考えるのである。管理者は実際にはほとんど物理的作業を行わないが、現業員の決定・行動に影響を与えることで、組織の目的の達成に貢献しているといえる(Simon, 1976, p.2 邦訳p.4)。つまり、このときの現業員は、さきほどのAさんがBさんに委譲してしまったように、意思決定の連鎖の一部を管理者に委譲してしまったことで、結果的に管理者の影響力に従っていることになる。このような現業員と管理者(非現業員)との間の意思決定職務の分業は、通常の「分業」である水平的専門化に対比して、垂直的専門化 (vertical specialization)と呼ばれ(Simon, 1976, p.9 邦訳p.12)、管理過程の観察が容易なので、しばしば取り上げられる。
以上のことから、このような意思決定過程における分業が、メンバーの意思決定状況の単純化に重要な役割を果たすとともに、あるメンバーが他のメンバーの影響にしたがうという点で、組織の管理過程にとっても本質的なものであるということがわかる。つまり、管理過程(administrative process)の本質は、組織メンバーの意思決定過程を構成するある意思決定前提をそのメンバーの意思決定過程から分離し、さらにこれらの意思決定前提を決定し、伝達してくれるメンバーを選択したり、当該メンバーが決定した内容を意思決定前提として必要とする関係のあるメンバーに伝達する正規の組織的手続きを確立するということにある。このとき見方を変えれば、組織は、組織メンバーの意思決定の自主権 (autonomy)の一部を取り上げ、そこに、組織の意思決定過程を置き換えたと見ることができるのである(Simon, 1976, p.8 邦訳p.11)。したがって、管理過程は垂直的専門化と呼ばれてはいるが、実際には垂直方向ばかりに存在するわけではなく、水平方向を含め、あらゆる方向に存在するものであるということには注意がいる。
こうした管理過程が確立されるということは、組織の中に身を置く人間が、組織内の他のメンバーからもたらされる意思決定前提によって構成される状況定義に基づいて、組織の観点からの意思決定を行うようになるということである。したがって、組織メンバーの状況定義形成の局面で重要な役割を担う現象面での2本柱として、少なくとも次のことは挙げられる必要がある。
そこで、この二つの現象について順に見ていくことにしよう。
状況定義形成の局面、特に「現実の世界」を単純化する際に、基本的に重要な役割を果たしているのが、一体化の現象である。個人の諸目的(goals)は、組織にとって所与の存在ではない。組織はメンバーを新規に採用する手続き(recruitment procedures)や組織内の実践(organizational practices)によって、メンバーの目的を操作することができると考えられる(March & Simon, 1958, p.65 邦訳p.100)。
その一方で、個人にとっても、一体化(identification)と呼ばれる現象がある。組織のメンバーが組織の観点から、あるいはその下位集団の観点から発言を行うことはごく普通にみられることである。大抵の人は、就職して会社に所属すると、ごく自然に「うちの会社は……」というような言い方をするようになる。さらに進むと、何か個人的な感想・意見を求められたときでさえも、こうした前置きをせずに、自分の所属する会社の立場からの発言をしてしまうような人も出てくるものである。このことを一般化して、より明確に定義すると、ある人が意思決定を行うにあたって、特定の集団にとっての結果の観点からいくつかの代替案を評価するとき、その人はその集団に自身を一体化しているというのである(Simon, 1976, p.205 邦訳p.260)。言い換えれば、メンバーが組織と目的や価値を共有しているとき、そのメンバーは組織に自身を一体化している状態にあるといえる。
ただし、ここで注意がいるのは、一体化の対象は必ずしも組織全体というわけではないということである。March & Simon (1958, pp.70-77 邦訳pp.109-118)は、組織の中のメンバーの一体化の主要な対象として次のものを挙げている。
このうち、3の課業集団は同じ課業を遂行している人の類(class)のことで、下位集団のこともあれば、組織外集団のこともある。また、4の組織外集団の例としては、労働組合(ただし、日本の場合は企業別組合なので、実質的には2に該当すると思われる)、コミュニティ集団、家族などがあげられる。
このように一体化の対象は様々であるが、様々であるからこそ、一体化は組織メンバーの状況定義形成の際に、どの程度の単純化が行われるのかを決める重要な要因となっている。いま、行動がはっきりと関係づけられ、行動の成果を評価する基礎を与える、という意味での「操作的な」(operative)目的を考えてみよう。こうした操作的な目的は、「現実の世界」がモデルに単純化され状況定義に結晶する際の核となるものなのであるが(Simon, 1976, p.xxxv 邦訳序文p.36)、操作的な目的のうち最高位の目的は、組織全体というより下位集団の目的であることも多い。この場合には、状況定義の単純化はより一層顕著なものとなる。つまり、そうした操作的な目的をもった下位集団に一体化することで、注意の焦点(focus of attention)が生まれ、その結果として、ある基準を排除して、他の下位目的、あるいは組織全体の目的の他の局面は無視するという選択的不注意(selective inattention)と、自分の所属している下位集団の目的に特別の注意を払う選択的注意 (selective attention)とが行われる。組織の下位集団で扱う問題は、組織全体で扱うべき問題に比べると既にかなり単純化されたものになっているので、操作的目的をもった下位集団に一体化することで、より容易に単純化が行われ、状況定義が形成されることになるのである(March & Simon, 1958, pp.152-154 邦訳pp.233-236)。
さきほどの図4.1の例でいえば、AさんがBさんによってもたらされた伝達内容である数件の賃貸物件を批判的な検討や考慮をすることなしに代替案として受容し、意思決定前提として用いる場合、Aさんは「Bさんは東京都内の住宅事情については権威だから……」などと理由づけをすることがある。この用語法の延長線上に、ここでいう権威の概念がある。
組織メンバーの状況定義形成の局面で重要な役割を担う現象としての権威は、日常語における権威よりも広くて一般的な概念として扱われる。一言で言ってしまえば、権威 (authority)とは何ら批判的な検討や考慮をすることなしに伝達(命令)を受容する現象をさしている。一般に、組織メンバーは「伝達された他人の意思決定によって、彼自身の選択が導かれることを許容し(すなわち、他人の意思決定が彼自身の選択の前提として役立つ)、これらの前提の便宜性(expediency)について、彼自身の側で考えることをしない、という一般的な規則を彼自身で設定している」(Simon, 1976, p.125 邦訳p.161)のである。このように組織メンバーが組織内での伝達を権威ある意思決定前提として受容することの最も大きな理由は、人間の限定された合理性にあるということは前述のとおりである。命令・信号といったものを吟味するのに必要な専門的知識を持っていないため、さらには、時間・労力の制約もあるために、組織内での伝達を権威あるものとして受容するのである。
こうした意思決定前提に関する議論からもわかるように、実は、権威の現象は単に上司から部下への伝達という場面だけに限定されて発生するものではない。もちろん上から下への伝達の場面が最も馴染みがあるのではあるが、水平的に伝達される場合にも、あるいは下から上に伝達される場合にさえも権威の現象は生じうる。例えば、会社の社長は社長秘書が整理・伝達する伝言、スケジュールや面会予約をなんら批判的な検討や考慮をすることなしに受容しているが、それは社長秘書の伝達が権威あるものとして社長に受容されていることを意味している。そこで、より正確にかつ一般的に権威の定義を考えれば、権威とは伝達の性格であり、「なんら批判的な検討や考慮をすることなしに示唆を受容するというすべての状況を意味するものと理解しよう」(Simon, 1976, p.128 邦訳p.166)ということになるのである。このようにして、組織メンバーは自分の意思決定の基礎となっているいくつかの諸前提を組織が決める(Simon, 1976, p.123 邦訳p.159)ことを受け入れ、自分の意思決定過程を単純化し、状況定義が形成される。
権威という現象を以上のような観点から説明すると、実は、権威を行使するときには上司は部下を納得(convince)させようと努めるのではなく、単に部下の黙認(acquiescence)を得ようとのみするということになる(Simon, 1976, p.11 邦訳p.15)。このことをより明確に示しているのが、無関心圏という概念である。Barnard (1938, pp.167-170 邦訳pp.175-178)はおのおのの組織メンバーには「無関心圏」(zone of indifference; 経済学的含意を考慮すると「無差別圏」と訳すべきだと思われるが、既に定訳になっている) が存在し、その圏内では命令の内容は意識的に反問することなく受容しうるのだと考えた。つまり代替案レベルでは、無関心圏が存在し、その圏内にある代替案に対しては、その内容については無差別で、それが何であるのかについて比較的無関心に、命令を受け入れるのである。例えば、全国各地に事業所があり、転勤して回ることが常であるような企業では、代替案である転勤先は通常は無関心圏に属し、「A市へ転勤」、「B市へ転勤」、……などの転勤先については比較的無差別で、無関心である。このように権威を行使するときには、上司は部下の納得を求めるのではなく、まさに、単に部下の黙認を得られればよいのである。この考え方は Simon (1976) にも「受諾圏」(zone of acceptance または area of acceptance)という概念で受け継がれている。
それでは無関心圏はどのようにして設定されるのであろうか。個人が組織へ参画する決定、および、組織が個人を受け入れる決定が行われるときについて考えてみよう。一般的には、March & Simon (1958, pp.90-93 邦訳pp.137-141)の考えている雇用契約 (employment contract)のような公式のものではなくても、心理的に誘因貢献の契約 (inducements/contributions contracts)がなされていると考えると理解がしやすい。すなわち、個人が組織に何を貢献し、何を受け取るのか、そして組織が個人に何を貢献し、何を受け取るのかについて、なんらかの設定を行って、個人が組織のメンバーとなると考えるのである(Thompson, 1967, p.105 邦訳p.135)。
この契約により、組織とメンバーとなる個人とのかかわりに制限が加えられる。個人の側からすると、
というように権限関係を受容し、無関心圏が設定されるのである(Thompson, 1967, p.106邦訳p.136)。この誘因貢献の契約は、個人の組織参画時だけではなく、組織への参加を継続する中でも、公式、非公式に何度か行い、そのたびに誘因貢献の契約内容が見直されていると考えるべきであろう。
誘因貢献の契約は、当該メンバーの側で無関心圏を設定するだけにとどまらず、他のメンバーの状況定義の形成にも重要な働きをしている。つまり、個人が組織的状況において示す行動に枠を設定することにより、組織の中における個人の異質性(heterogeneity)の表出を減少させるのである(Thompson, 1967, p.105 邦訳p.135)。こうして組織のメンバーシップを明確にし、組織参画の際の誘因貢献の契約を行うことで、ある意味での組織メンバーの意思決定や行動の均質化・標準化が行われ、他のメンバーの状況定義の単純化にも寄与することになるのである。
この章の最後に、この節では、Takahashi & Takayanagi (1985)に基づいて、同時方式と逐次方式という二つの意思決定方式を採用した簡単な意思決定モデルを作り、そこから導出された仮説を実際の調査データで検証することにしてみよう。この二つの意思決定方式は、組織の中の人間の行動を考察する際に、多くの場合は暗黙のうちにどちらかに仮定されているために、その比較はほとんど明示的に取り扱われてこなかった。
議論を明確にするために、意思決定過程の構造を考えて、意思決定方式がどのように意思決定過程にかかわっているものであるかを示すことにしよう。意思決定過程は決定理論に基づけば古典的には次のような四つの局面に分けて記述することができる(cf. Lindblom, 1968, ch.3)。
《意思決定の4局面》これらの各ステップは、それぞれがそれ自体で一つの過程を構成しているが、ここで扱う二つの意思決定方式の違いは、このうち主として2の過程に関したものである。
いまこの2のステップで s 個の代替案を探索して揃えて、その上で3、4のステップに進み、同時に比較検討を行ない、その s 個の代替案のうちの一つを選択するとしよう。こうした方式を同時方式と呼ぶ。同時方式は、とられる代替案の数が探索に先だってあらかじめ s と固定され、その s を探索過程の中で変えないことになるので、固定サイズ方式(fixed-size procedure)とも呼ばれる(Takahashi & Takayanagi, 1985)。
一方、2のステップで代替案を一つだけ探索し、そのままステップ3、4に進み、ものその代替案がある受容可能な達成水準に達するならば、その代替案を選択し、もし達しないならば、また2のステップに戻って、もう一つの代替案を探索し始めるというように、一つの代替案ごとにステップ2、3、4を繰り返すならば、こうした方式は逐次方式(sequential procedure)と呼ばれる。この場合には、同時方式とは異なり、探索されるべき代替案数を前もって決めることはしないで、代替案の出来次第、結果次第で探索される代替案数が変動することになる。
こうした意思決定方式に対する考え方の原型は、例えば、Blackwell & Girshick (1954)のような統計的決定理論の中に登場する二つのサンプリングの方法、すなわち、固定サイズ方式(fixed sample-size procedure)と逐次方式(sequential sampling procedure)である。固定サイズ方式では、サンプルをとる前からサンプルの大きさが決まっている。それに対して、逐次方式では、一つのサンプルをとるたびに、それまで集めた情報に基づいて、 (i) サンプルをとることを中止して決定を下すか、(ii) 少なくとももう一つのサンプルをとるか、という判断を逐次下していきながらサンプリングが行なわれる。ここでの代替案の探索に関する同時方式と逐次方式は、これらの二つのサンプリングの方式に対応している。
探索(search)の問題は広く研究されているが(例えば、DeGroot (1970)あるいは、 Lippman & McCall (1976)のサーベイ論文を参照されたい)、ここでは後述する仮説を導くために、必要最小限度のモデルを考察することにしたい。意思決定方式のモデル化に際して、意思決定の4局面のうち4について、満足基準の仮定を置いておくことにしよう。すなわち、4の「目的・価値を最大化するような代替案、もしくは、ある受容可能な達成水準に達する代替案を選択する。」とあるうちの、後者の方だけを、つまり、ある受容可能な達成水準に達する(すなわち満足できる)代替案を選択すると仮定するのである。いま、代替案がある条件を満たすときは利益wをもたらすが、少しでも条件に合わなければ何も利益をもたらさないとしよう。つまり、満足できる代替案のもたらす利益は w、不満足な代替案のもたらす利益は0とする。また一つの代替案を探索・検討するのに要する費用を c とする。
まず最初に、同時方式をとる場合について考えてみよう。固定された代替案数を s とする。代替案 i (i=1, ..., s)について、次のような確率変数 Zi を考える。
| w | ・・・・・・代替案 i は満足 | |
| Zi= | ||
| 0 | ・・・・・・代替案 i は不満足 |
そして、確率変数 Z1, Z2, ..., Zs は独立同分布であると仮定し、
Pr(Zi=w)=p
Pr(Zi=0)=q=1-p
とする。
代替案数が s であるから、s 個の代替案の中に少なくとも一つは満足できる代替案のある確率は、1-qs で表される。したがって、同時方式で、代替案数をあらかじめ s としておいたときの期待利得 R(s) は、
R(s)=w(1-qs)-cs
で表される。この式から、同時方式での最適代替案数 s* は、s を連続変数と考えて、近似的に求めることができる。すなわち、R(s) を s で微分して0とおくと、
wqs・log q+c=0
となるので、これを満たす s を求めると、
s=[log{-c/(w log q )}]/ log q
最適代替案数 s* は R(s) を最大にする正の整数なので、いま求めた s を使えば、明らかに、
s-1≦s*≦s+1
であることがわかる。同時方式をとる場合には、代替案数をこのようにして求めた s* に設定することが最適である。ある程度の代替案数を揃えなければ、満足できる代替案は見つからないだろうし、逆に満足できる代替案が複数あっても仕方ないので、あまりたくさん探索ばかりしていても、探索・検討の費用がかさむだけだからである。
次に、逐次方式をとれば、この同時方式のときの最大期待利得 R(s*) よりも、期待利得をさらに大きくすることができる。最大 s* 個までは代替案を探索・検討することにして、代替案を探索1回につき一つだけ探索・検討し、もしその代替案が満足できるものであるときには、その代替案を選択し、即座に探索を打ち切ってしまえば、意思決定者は探索・検討する代替案の数を減らすことができる。なぜなら、この逐次方式をとったときに s* 個の代替案をすべて探索・検討しなくてはならないのは、最初の代替案から s*-1 番目の代替案まで、立て続けに不満足なものばかりが続いたときだけに限られるからである。つまり
Z=(Z1, Z2, ..., Zs*)
とすると、その標本空間 S は
S=S1×S2×……×Ss*
となる。ただし、Si は Zi の標本空間で、
Si={0, w}, i=1, 2, ..., s*
であるから、S は 2s* 個の点からなっていることになる。そのうち、s* 個の代替案すべてを探索・検討しなくてはならないのは、
(0, 0, ..., 0, 0), (0, 0, ..., 0, w)
の2通りの場合のみにすぎないのである。より正確には、逐次方式をとったときの探索過程の停止時点までに探索・検討した代替案数 N を確率変数とすると、その期待値は、
| E(N) | =Σn=1s* nqn-1p+s*qs* |
| <Σn=1s*s*qn-1p+s*qs* | |
| =s*(1-qs*)+s*qs* | |
| =s* |
以上のことから、次の仮説を立てておくことにしよう。
仮説4.1 逐次方式で行なわれる決定の方が同時方式で行なわれる決定よりも探索・検討される代替案の数が少ない。
この仮説4.1の検証、および意思決定方式の実態を調べるために、調査が企画、実施された。調査は郵送質問票を用い、国内の全上場企業と生命保険会社、計1,781社を対象として行なわれた。質問票は1983年1月5日に発送され、2月10日までの回収分をデータとして使用した。回収は299社、回収率は16.8%であった。
調査票には仮説4.1を検証するために、次のような質問を用意した。
Q4.1 貴社が最近行なった、工場・支社・営業所等の移転・新設の決定は、次のどちらの型のものでしたか。一つだけお選び下さい。
この質問は、工場・支店・営業所等の移転・新設の決定についてのものであるが、ここで立地計画案の決定に質問を限定したのは、これならば、製造業、非製造業、あるいは業種の別を問わずに行なわれているだろうと考えたためである。
そこでまず、その調査結果を企業が同時方式と逐次方式をどの位の比率で採用しているのかについて業種別にまとめたものが表4.1である。この表4.1でわかるように、全体では58.4%の企業が同時方式と答え、41.6%の企業が逐次方式と答えている。業種別にはバラつきが大きいが、「建設」「生保」を除いたすべての業種で同時方式が多数を占めている。逐次方式はむしろ少数派なのである。
表4.1 意思決定方式と検討された代替案数
| 産業 | 意思決定方式(%) | 代替案数の平均 | オブザーべ ーション数 | |||
|---|---|---|---|---|---|---|
| 同時方式 | 逐次方式 | 同時方式 | 逐次方式 | |||
| 建設 | 25.0 | 75.0 | 2.40 | 2.79 | 27 | (19) |
| 食品 | 53.8 | 46.2 | 2.86 | 2.33 | 16 | (13) |
| 繊維 | 66.7 | 33.3 | 2.63 | 2.00 | 12 | (12) |
| 紙・パルプ・化学・石油 | 66.7 | 33.3 | 5.31 | 3.00 | 30 | (23) |
| 鉄鋼・非鉄金属 | 63.2 | 36.8 | 3.08 | 3.00 | 23 | (19) |
| 機械 | 60.0 | 40.0 | 2.94 | 2.83 | 36 | (29) |
| 電機 | 52.6 | 47.4 | 3.90 | 3.44 | 25 | (19) |
| 造船・自動車 | 60.0 | 40.0 | 4.33 | 2.25 | 12 | (10) |
| 精密機械 | 66.7 | 33.3 | 3.33 | 2.00 | 11 | (8) |
| 商社・百貨店・スーパー | 53.8 | 46.2 | 3.00 | 4.78 | 28 | (23) |
| 銀行 | 73.7 | 26.3 | 17.58 | 5.75 | 22 | (16) |
| 証券・損保 | 70.0 | 30.0 | 3.33 | 2.00 | 11 | (8) |
| 生保 | 40.0 | 60.0 | 5.50 | 4.67 | 5 | (5) |
| 公益事業 | 62.1 | 37.9 | 3.76 | 2.88 | 41 | (25) |
| 全体 | 58.4 | 41.6 | 4.77 | 3.16 | 299 | (229) |
しかし、意思決定方式ごとの代替案数の平均は「建設」「商社・百貨店・スーパー」を除いたすべての業種で、逐次方式の方が少なくなっている。全体での平均も、同時方式では4.77、逐次方式では3.16となっていて、平均値の差の検定を行なってみると、t=1.94 ( p=0.052)で、統計的に有意な差があった。したがって、仮説4.1の通り逐次方式の方が代替案数は少なくなっていることがわかる。
代替案数では「銀行」の同時方式の17.58が飛び抜けて大きな値になっているが、これは銀行の支店設置が許認可の対象となっていることと関係があると考えられる。「銀行」の同時方式の比率が73.7%と業種別には一番高くなっていることも、「銀行」の支店立地をめぐるこうした特殊事情が背景にあると考えられる。
逐次方式の方が、代替案数が少なくて済むということが、理論的にも実際の調査データでも確認されたにもかかわらず、実際には同時方式の方が多数派を占めるということは、モデルでは考慮していなかった何か他の理由があると考えるべきであろう。このことについては、興味深い事実発見が得られている。意思決定方式と部門間のコンフリクトの解決方法との間に関連のあることがわかったのである。部門間コンフリクトということで、質問の対象は製造業だけになっているが、次のような質問が用意された(cf. 加護野, 1980)。
Q4.2 新製品開発や製造工程革新の決定に際して、貴社では、部門間の調整をどのようにして行なったでしょうか。該当するものを一つだけ選んで下さい。
選択肢のうち、1は「会議」、2は「上司」、3は「根回し」によるコンフリクトの解決ということになる。調査結果は表4.2に示されている。この表からもわかるように、部門間コンフリクトの解決方法として「会議」「根回し」をとる企業では同時方式が多くとられ、「上司」によるコンフリクト解決を行なう企業では逐次方式が多くとられるということがわかる。なぜこのような現象が観察されるのかは、次の第5章の数理的組織設計論で証明される定理5.1の分離定理によって明らかにされることになる。実は、全体としての意思決定過程が逐次方式で行なわれている場合でも、同時方式の決定問題に直面する意思決定者が現れるのである。
表4.2 意思決定方式と部門間コンフリクトの解決方法
| 部門間コンフリ クトの解決方法 | 意思決定方式 | ||
|---|---|---|---|
| 同時方式 | 逐次方式 | 計 | |
| 会議 | 15(83.3) | 3(16.7) | 18(100.0) |
| 上司 | 16(39.0) | 25(61.0) | 41(100.0) |
| 根回し | 51(68.9) | 23(31.1) | 74(100.0) |
| 計 | 82(61.7) | 51(38.3) | 133(100.0) |
以上のように、満足方式と逐次方式は必ずしも結びついたものではない。経営人モデルが主張するように、現実の人間にとっては満足基準のみが可能な選択肢であるが、逐次方式と同時方式はともに組織現象として理論的にも実際にも存在しうる意思決定方式なのである。
組織設計の概念は、最初はコンティンジェンシー理論(contingency theory)と呼ばれる分野で形成されてきたものである。Lawrence & Lorsch (1967)は、経験的データに基づき、かつ最善の組織形態が組織の環境的条件によって条件づけられているという主張を明確に打ち出した一連の経営組織研究に対してコンティンジェンシー理論の名称を与えた。
コンティンジェンシー理論の原型は Burns & Stalker (1961)まで遡る。彼等は調査結果に基づき、機械的システム(mechanistic system)と有機的システム(organic system)という管理システム(management system)の二つの理想型を見出し、前者は安定的で不確実性が低い環境下で効率的で、後者は不安定で不確実性が高い環境下で効率的であると主張した。ここで、彼らの機械的システムは部下の活動がその上司によって調整され、調整を行う際には、情報が上位層に独占的に集中するというような特徴をもっている。また有機的システムは部下の活動の調整が、部下間の相互作用を通して行われ、その際の情報は特定問題ごとに定められた統制・権限・伝達のセンターに集められるという特徴をもっている。
一方、1960年代にはマトリックス組織と呼ばれる組織構造が登場したが、Davis & Lawrence (1977)は従来のピラミッド型の組織と対比させてマトリックス組織の調査研究を行い、マトリックス組織がピラミッド組織に比べて望ましいものとなる必要条件は不確実性が高いことであると主張している。
これらの研究例からもわかるようにコンティンジェンシー理論は、環境の不確実性と、それに適した組織形態との関係を見出すという点で成果を挙げてきたが、その議論はもっぱら実証研究に基づくものであるために、そこで「命題」と呼ばれているものの大部分は、実は、単に調査結果からの推論として引き出されたものにすぎない。それ故、組織設計論の分野では規範的アプローチをとった研究がほとんどないという指摘が従来からなされている(例えば、Hax & Majluf (1981))。他方、不確実性をともなった環境の下での「組織」の数学的モデルについては、Marschak & Radner (1972)に代表される何人かの主に経済学者によって決定理論の延長線上で研究されてきているが、これらの研究はコンティンジェンシー理論とは独立に、かつ無関係に行われていたために、コンティンジェンシー理論に対する貢献はほとんどない。
コンティンジェンシー理論、そして組織設計への何らかの貢献を意図するならば、組織設計問題を組織論の概念的枠組みの中で定式化すること、そしてそこから得られた結果のコンティンジェンシー理論的な含意に注意を払うことが必要である。そこで、この章では、Takahashi (1987, chs.1-2; 1988)に基づいて、組織論、特に経営組織論における組織設計の問題を統計的決定理論の視点から考察することにしたい。
第4章でも述べたような組織の中で意思決定者が用いるモデルである状況定義は、特定の組織形態と結び付いた形で存在することになる。したがって、組織形態による違いをこの状況定義の中に組み込むことで、組織設計論と決定理論とを結び付け、第1章~第3章で議論してきたような決定理論的アプローチにより不確実性下における効率的組織形態を考察することができる。そこでこの章では、まず組織設計における重要な問題を組織論の枠組みの中で統計的決定問題の中に組込んだ形で定式化する。そして、このモデルを分析することで、不確実性下における効率的な組織形態についてのいくつかの命題を導出しよう。
ここでは組織における課業の逐次決定問題が、経営組織論の概念的枠組みの中で定式化される。二つのタイプの組織構造(ピラミッド組織とマトリックス組織)は課業の割り当てのシステムとして、二つのタイプの管理システム(システム1とシステム2)はコミュニケーション・システムとしてそれぞれ定義され、課業の逐次決定問題のモデルの中に組み込まれる。
ここでは次の三つの階層からなる組織が考えられる:
n 個の単位組織は共に組織全体の資源に依存し、かつ各単位組織の活動の実行のタイミングも相互に関連しているなど、単位組織間には相互依存性があるので、単位組織の活動は計画を組んで調整する必要がある。いま単位組織 i によって実行されるべき活動(activity)を ai として、Ai をすべての ai の集合としよう。すると、組織全体での活動である組織的活動 (organizational activity)は a=(a1, ..., an) で表され、A=A1×・・・×An は組織のもつ活動のレパートリー(repertory)を表すことになる。
ここで、各マネジャーは組織の中で、ある特定の地位を占めるとともに、トップ・リーダーに対して組織全体の活動計画について自分の部門的・専門的な観点から助言・勧告をする役目をもっている。そこで、次の仮定をおくことにしよう。
仮定5.1 各マネジャーはある組織的活動をトップ・リーダーに推薦する。
ここで、マネジャー i によって推薦された組織的活動 ai を課業(task)と呼ぶことにし、A'={a1, ..., am} と定義する(A'⊂A)。A' はマネジャーによって特殊化・専門化された課業の集合なので、専門化されたレパートリー(specialized repertory)と呼ぶことにする。
古典的な経営管理論では命令系統一元化の原則(principle of unity of command)が唱えられていた。例えば、古典的かつ代表的な経営管理論の教科書であるKoontzのPrinciples of Managementの第7版になるKoontz, O'Donnell & Weihrich (1980, p.427)では「一人の部下がただ一人の上司に報告をするという関係が、より完全であればあるほど、命令の際にコンフリクトの問題が起こることはより少なくなり、結果に対する個人の責任感はより大きくなるものである。」と命令系統一元化の原則を述べている。この原則に従えば、命令の際のコンフリクトの発生を抑え、かつ個々人の責任感を強くするためには、部下たるものは必ず一人の上司にのみ仕えなくてはならない。ピラミッド組織(pyramid organization)とはまさにその原則に則った組織であり、その中では、単位組織は唯一人のマネジャーが定めた課業を遂行することになっていて、したがって、トップ・リーダーは集合 A'={a1, ..., am} の中から一つの課業を選択しなければならないことになる。
しかし、高価でかつ高度に専門化した人的資源を含む資源の有効的な利用をめざして、現存の手持ち資源をいくつかの課業の間で、命令系統一元化の原則にこだわらずにもっと融通を利かせて運用し、同時に複数の課業につかせたり、次から次へと容易に課業を代われるようにしておくことが考えられるようになり(Davis & Lawrence, 1977; Janger, 1979)、マトリックス組織(matrix organization)と呼ばれる組織が登場してくることになる。
Davis & Lawrence (1977, p.3)はマトリックス組織を、多元的命令系統を採用し、命令系統一元化の教えを捨てた組織であると定義した。この定義に従えば、マトリックス組織とは、少なくても二人のマネジャーが権限のラインに位置している組織であり、トップ・リーダーは各単位組織に対して、それらラインにあるマネジャーによって推薦された二つ以上の課業をある割合で、もしくはある分布にしたがって実行するように命令することになる。すなわち、トップ・リーダーはマネジャー間のパワー分布を決定する。このことは Davis & Lawrence (1977, p.77: 邦訳 p.121)が「マトリックス組織では二元的圧力が存在するために、その圧力をともに考慮した、バランスのとれた意思決定が必要となる。このような意思決定を実現していくうえで、トップ・リーダーの果たすべき決定的に重要な役割はマトリックスに存在する二つの系統間のパワーの合理的バランスを定め、維持することである。」と述べているように、マトリックス組織におけるトップ・リーダーの決定過程を特徴づけるものである。
こうした割合、分布を表すために、A'={a1, ..., am} 上の確率分布として混合課業(mixed task)を定義する。混合課業 f=( f1, ..., fm) は A' の要素 a1, ..., am を f1, ..., fm の割合で混合したもので(ただし、fi≧0、Σi fi=1)、すべての混合課業 f の集合を F とする。もし、トップ・リーダーが混合課業 f=( f1, ..., fm) を選んだとすると、十分に長い期間の間では、各単位組織はその作業時間の 100 fi % をマネジャー i の命令の下で作業することになる。トップ・リーダーは f を決めることでマネジャー間の権限及びパワーの分布を決定することになる。また、ある1点 ai に確率1を与えるような確率分布 f を純課業(pure task)と呼び、ai∈A' をこの f と同一視すると、純課業の集合 A' は混合課業の集合 F の部分集合となっている。
組織構造は、確率分布 f∈F で表される課業の割り当てのシステムと定義されるが、ここではピラミッド組織とマトリックス組織の二つのカテゴリーに分類することにする。もし組織の実行する課業が A' に属する純課業であれば、その組織はピラミッド組織と呼ばれる。もし組織の実行する課業が F-A' に属する混合課業であれば、その組織はマトリックス組織と呼ばれる。したがって、トップ・リーダーが A' からある純課業を選択したならば、ピラミッド組織を採用したことになるし F-A' からある混合課業を選択したならば、マトリックス組織を採用したことになる。
図5.1はマネジャー3人、単位組織5つのケースについて、ピラミッド組織の例(a)とマトリックス組織の例(b)を図示したものである。この図では権限のラインは線で示されているが、(b)のマトリックス組織の中にある権限のラインのうち、(a)のピラミッド組織の中では機能していないものがあることに注意されたい。
図5.1 ピラミッド組織とマトリックス組織
(a)ピラミッド組織 (b)マトリックス組織
経営管理論では (cf. Koontz, O'Donnell & Weihrich, 1980)、ラインとスタッフの区別は単なる関係の問題であると考えられている。ライン(line)と呼ばれるものの本質は上司が部下を直接監督するという権限関係であるのに対して、スタッフ(staff)は単に助言・勧告を行う関係である。もし fi>0 ならば、マネジャー i は単位組織の部下たちに対してライン権限を与えられていることになる。しかし、もし fi=0 であれば、マネジャー i はトップ・リーダーに単に課業の勧告をしただけにすぎず、スタッフの関係しかないということになる。このように部下に対して権限をもたないマネジャーはナル・マネジャー(null manager)と呼ばれる (Takahashi, 1986)。ピラミッド組織では、トップ・リーダーは各単位組織に対して、唯一人のマネジャーにのみ貢献し、その課業だけを遂行するように命令するので、それ以外の他のマネジャーには権限が与えられず、ナル・マネジャーということになる。それ故、図5.1(a)のピラミッド組織のように一人のマネジャーにラインとして全権限が与えられ、他のマネジャーはラインからはずされて、スタッフとしての関係しかない組織はライン・スタッフ組織(line and staff organization)と呼ばれている。この図5.1(a)では、マネジャー1と3は部下を持たず課業に関する権限も持たない。すなわち、彼等はトップ・リーダーを単にスタッフとして補佐しているだけのナル・マネジャーとなっていて、この図はライン・スタッフ組織の一例である。ナル・マネジャーは日本企業で「スタッフ課長」などと俗称されているものに相当する。
マトリックス組織の登場は、米国政府が航空宇宙産業に対して研究開発契約の受諾条件として、プロジェクト管理方式を課したことに端を発しているといわれている(Kingdon, 1973)。この航空宇宙産業に代表されるようなプロジェクト単位で仕事をしてきた企業では、ピラミッド組織を基本としながらも、新しいプロジェクトに対しては、そのピラミッド組織に重複、横断する形でプロジェクト・チームを組織して、ひとたびプロジェクトが終了するとプロジェクト・チームを解散し、構成メンバーをピラミッド組織の本来の所属に戻すというやり方で、一時的ではあるが複元的な命令系統がみられるようになった。こうした発展段階を経て、米国の宇宙開発が盛んだった1960年代の航空宇宙産業においてマトリックス組織が誕生したといわれている(Davis & Lawrence, 1977)。
しかし、マトリックス組織がピラミッド組織に比べて比較的最近考案されたものであるという理由だけで、ピラミッド組織を時代遅れで非効率なものであると考えるべきではない。確かにマトリックス組織は人的資源及び設備の有効的な共有と運用とによって、より高い業績を挙げることができるかもしれないが、はたしてピラミッド組織と比べてどの程度、そして、どういう場合に効率的になるのかを論理的に考えていく必要がある。そのこと次第では命令系統一元化の原則が生きてくる可能性がある。
同じ課業であっても、組織にとって制御不可能な諸要因のために異なる結果を生むことがある。これらの諸要因は第2章で議論したように、環境(environment)と呼ばれる。いま環境の状態(state of environment)を θ で表し、環境のすべての可能な状態の集合を Ω={θ1, ..., θs} で表すことにする。トップ・リーダーはこうした環境の状態を考慮に入れつつ、課業の調整と計画を行う必要がある。
そこで、同じ課業でも環境の状態によって異なる結果を生む、ということを表現するために、損失関数(loss function)を考え、これを Ω×A' 上で定義された非負関数 L(θ, a) として表すことにする。損失は負の効用で、混合課業 f=( f1, ..., fm) の損失は
L(θ, f )=Σi fi L(θ, ai)
によって与えられることにする。そこで、次の仮定をおくことにする。
仮定5.2 トップ・リーダーとマネジャーは同じ損失関数をもっている。またトップ・リーダーとマネジャーは環境の状態について、同じ事前分布 w=(p(θ1), ..., p(θs)) をもっている。ここで、p(θi) は状態 θi の主観確率である。
このように、環境の状態については不確実性が存在しているので、各マネジャーが単位組織を通して環境の状態についての観測をすることを考えよう。まず、マネジャー i によって得られる観測結果(observation)をその分布が環境の真の状態に依存する離散型確率変数 Xi として表し、その標本空間を SXi とする。そして、各マネジャーが接しているのは環境の一部にすぎないので、全マネジャーの観測結果を集めて Z=(X1, ..., Xm) と組にして組織的観測結果(organizational observation)として利用することにする。組織的観測結果の標本空間は SZ=SX1×・・・×SXm となる。尤度関数 p(z|θ) は既知であると仮定する。
組織的観測結果を形成するに際して、マネジャーの観測結果を収集する二つの代替的な手続きが考えられる:
言い換えれば、組織には観測センター(observation center)の配置に関して二つの代替的配置があるということである。手続き1ではトップ・リーダーが観測センターを兼ねることになる。それに対して手続き2では、ある一人のマネジャーが観測センターとなる。つまり、課業の決定については、トップ・リーダーが権限をもっているが、情報収集というより技術的でオペレーショナルなサンプリングの決定権に関しては、マネジャーに委譲するのである。
Burns & Stalker (1961)は組織がその各メンバーに対して彼自身と他のメンバーの行為を制御する権利と制御される義務、そして情報を受ける権利と伝える義務とを与え、定める機構として管理システムを定義した。同様にしてここでは、二つの観測手続きを実現させるものとして理想型の管理システムを定義しよう。いま、トップ・リーダーが観測センターを兼ねるような管理システムをシステム1 (System 1)、ある一人のマネジャーが観測センターを勤めるような管理システムをシステム2 (System 2)と定義する。後で§5.3でも触れるが、システム1とシステム2は、それぞれ Burns & Stalker (1961)の機械的システムと有機的システムの特徴の一部をもったものである。
単純化のため、コミュニケーションのチャンネルはノイズレスであると仮定する。しかし、観測結果を伝達するには費用がかかる。組織のメンバーは賃金をもらっているので、伝達を行なっている間にも当然賃金は払われていることになる。さらに、トップ・リーダーが課業についての最終決定を下すまで、生産ラインが停止しているような状況下では、コミュニケーションの時間は即コストを意味する。実際、日本企業の工場の中には、QCサークルのメンバーによって停止時間当たりの発生コストを機械ごとに掲示している所もある。そこで、情報コストに関して、次のような仮定を置く。
仮定5.3 (1)各マネジャーは単位組織を通して、コスト cI で環境の状態についての観測を行う。(2)トップ・リーダーとマネジャーとの間のコミュニケーション・コストは cT、マネジャー同士間のコミュニケーション・コストは cM で、cT≧cM。
実際、Simon (1976, p.236 邦訳p.299)は、意思決定を分権化する理由として、「上司は部下よりも高い給与を受けているであろう。上司の時間は、組織の仕事のより重要な側面に留保しておかねばならない。もし、上司がある特定の意思決定を行うために、より重要な意思決定に使われるべき時間を犠牲にしなければならないのであれば、前者の意思決定の正確さがより増したとしても、それはあまりに高価につきすぎることになろう。」と述べている。常識的に考えても、トップ・リーダーとマネジャーとの間のコミュニケーションに要するコストはマネジャー同士の間でのそれと比べて単位時間当り賃金の点でも、機会費用の点でも大きくなっているはずである。したがって(b)のような関係を仮定した。
ここで、意思決定過程は、観測センターが次の二つの行動から一つの行動を逐次的に選ぶ決定過程として、より正確に定式化される。
行動1を観測行動(inspect action)、行動2を停止行動(stop action)と呼ぶことにする。このような組織の意思決定問題は、Wald (1947)によって創始された逐次決定問題 (sequential decision problem)として定式化される。ここでいう「逐次」とは、§4.3で述べた逐次方式のことである。
いま、 Z1, Z2, ... が独立同分布の確率変数列であるとする。ここで、Zj は j 番目に観測される組織的観測結果を表していて、その標本空間は SZj で示される。このうち、最初の j 個の組織的観測結果 Z1=z1, ..., Zj=zj を観測した後の事後分布 (posterior distribution)を
wj=(wj(θ1|z1, ..., zj), ..., wj(θs|z1, ..., zj))
で表すと、ベイズの定理、第3章の(3.6)式、(3.8)式から
w0(θi)=p(θi)
w1(θi|z1)=w0(θi)p(z1|θi) /[Σk w0(θk)p(z1|θk)] (5.1)
wj(θi|z1, ..., zj)=wj-1(θi|z1, ..., zj-1)p(zj|θi) /[Σk wj-1(θk|z1, ..., zj-1)p(zj|θk)], j=2, 3, ...
さらに決定ルールを定義しよう。
すなわち、z1, ..., zj が観測された後に停止行動がとられると、課業が分布 dj(z1, ..., zj) に従って選択されるのである。また、SZ1×・・・×SZj から A' への写像 dj'(z1, ..., zj) は最終純決定関数(terminal pure decision function)と呼ばれ、この最終純決定関数からなる関数列 d'=(d0', d1'(z1), d2'(z1, z2), ...) は最終純決定ルール(terminal pure decision rule)と呼ばれる。すべての最終決定ルールの空間を D、すべての最終純決定ルールの空間を D' で示すと、最終純決定ルールは最終決定ルールの特別な場合なので、D'⊂D が成り立つ。
ところで前項での定義からわかるように、管理システムによって観測センターの配置が異なるので、コミュニケーションのパターンもコミュニケーション・コストを含んだ情報コスト(information cost)も異なることになる。それぞれのコミュニケーション・パターンは、観測行動フェーズと停止行動フェーズの二つの行動のフェーズに対応して、図5.2に図示される。この図のシステム2ではマネジャー2が観測センターとなっている。
図5.2 システム1とシステム2
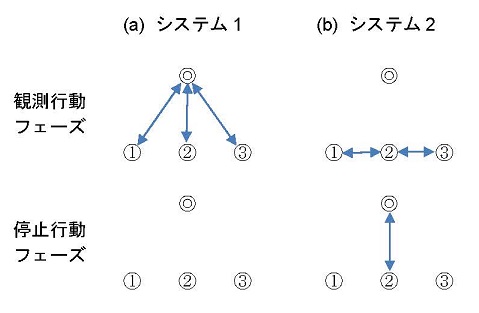
仮定5.3から、観測行動をとり組織的観測を1回行うと、システム1では
C1(I )=mcI+mcT
のコストがかかり、システム2では
C2(I )=mcI+(m-1)cM
のコストがかかる。ここで m は§5.1.aで定めたマネジャーの数である。また、停止行動がとられると、システム1では C1(S)=0 のコストがかかり、システム2では C2(S)=cT のコストがかかる。
停止ルール q=(q0, q1(z1), q2(z1, z2), ...) に対応して、
Q0=q0,
Qj(z1, ..., zj)=(1-q0)・・・(1-qj-1(z1, ..., zj-1)) qj(z1, ..., zj), j=1, 2, ...
のように関数列 Q=(Q0, Q1(z1), Q2(z1, z2), ...) を定義することにしよう。すると、 Qj(z1, ..., zj) は Z1=z1, ..., Zj=zj が与えられたときに、最初の j-1 個の組織的観測が行われるまで観測過程が停止せず、かつ j番目の組織的観測が行われた後に観測過程が停止する条件付確率を表している。
いま、停止時刻を表す確率変数(random stopping time)を N で表すと、期待停止時刻は
E(N)=Σj=0∞j E{Qj(Z1, ..., Zj)|w0}
で与えられる。期待情報コストが有限となるために、E(N) は有限であると仮定しておく。
以上のようなことから、任意の事前分布 w0 と任意の決定ルール (q, d) に対して、リスク(risk)と呼ばれる期待損失は次のように定義される。
rk(w0, (q, d))=Σi=1s w0(θi)Σj=0∞ E{Qj(Z1, ..., Zj)×[L(θi, dj(Z1, ..., Zj))+jCk(I )+Ck(S)]|θi} (5.2)
ここで、k はトップ・リーダーがシステム1をとるならば k=1、システム2をとるならば k=2 の値をとる。
効率的組織形態の議論に入る前に、手順として、リスクを最小にする決定ルールの存在を明らかにしておく必要がある。いま、ある与えられた事前分布 w0 と管理システム k について
Vk(w0)=inf(q, d)rk(w0, (q, d))
と定義する。もし各 w0 に対して
rk(w0, (q*, d*)) =Vk(w0)
であるならば、決定ルール (q*, d*) は、ベイズ決定ルール(Bayes decision rule)といわれ、Vk はベイズ・リスク(Bayes risk)といわれる。Takahashi (1987)によって、このベイズ・リスクが満たす関数方程式(functional equation)と、ベイズ決定ルールの存在とが証明されている。
いよいよ統計的決定問題として定式化された組織設計問題を解くことにしよう。ここで考える組織設計問題とは、ある事前分布w0に対して、リスク rk(w0, (q, d)) を最小にする決定ルール (q, d) (すなわち組織構造 d)と管理システム k とを見出すことである。
いま、Z1=z1, ..., Zj=zj が与えられたときの条件付期待損失(conditional expected loss)
E{L(Θ, dj(z1, ..., zj))|Z1=z1, ..., Zj=zj}=Σi wj(θi|z1, ..., zj) L(θi, dj(z1, ..., zj))
を最小にする最終決定ルールはベイズ最終決定ルール(Bayes terminal decision rule)と呼ばれ、そのときの条件付期待損失をベイズ期待損失(Bayes expected loss)という。
ピラミッド組織の中で達成可能なベイズ期待損失とマトリックス組織の中で達成可能なベイズ期待損失とを比較し、より小さなベイズ期待損失を達成する組織構造を効率的 (efficient)と呼ぶと、次の分離定理(separation theorem)が証明される(Takahashi, 1987)。
定理5.1 (分離定理) 効率的組織構造は、次のような意味において、管理システムから独立である。すなわち、任意の固定された q と k について、ベイズ最終決定ルール d*=(d0*, d1*, d2*, ...) は rk(w0, (q, d)) を最小にする。
《証明》(5.2)式の定義から、リスクは次のように書くことができる。
rk(w0, (q, d))=Σiw0(θi)ΣjE{Qj(Z1, ..., Zj) L(θi,dj(Z1, ..., Zj))|θi}+Σiw0(θi)ΣjE{Qj(Z1, ..., Zj)[ jCk(I )+Ck(S)]|θi} (5.3)
w0 と q, k はともに与えられているので、(5.3)式を最小にするためには、その第1項である次の式を最小にするような dj, j=0, 1, 2, … を選べばよい。
Σi w0(θi)Σj E{Qj(Z1, ..., Zj) L(θi, dj(Z1, ..., Zj))|θi}
=Σi w0(θi) ΣjΣ(z1, ..., zj) Qj(z1, ..., zj)×L(θi, dj(z1, ..., zj))p(z1, ..., zj|θi)
=Σi ΣjΣ(z1, ..., zj) Qj(z1, ..., zj)×L(θi, dj(z1, ..., zj))p(z1, ..., zj, θi)
=ΣjΣ(z1, ..., zj) Qj(z1, ..., zj)×[Σi L(θi, dj(z1, ..., zj))wj(θi|z1, ..., zj)] p(z1, ..., zj)
=ΣjΣ(z1, ..., zj) Qj(z1, ..., zj)×E{L(Θ, dj(z1, ..., zj))|Z1=z1, ..., Zj=zj} p(z1, ..., zj) (5.4)
この(5.4)式を最小にするためには、
E{L(Θ, dj(z1, ..., zj))| Z1=z1, ..., Zj=zj } (5.5)
を最小にするような dj を選べばよいことになる。定義から、この(5.5)式を最小にする最終決定関数はベイズ最終決定関数 dj* である。したがって、ベイズ最終決定ルール d*=(d0*, d1*, d2*, ...) は rk(w0, (q, d)) を最小にする。□
この分離定理は組織構造の設計問題における最適最終決定ルール d* を管理システム k、停止ルール q とは独立に求めることができるということを述べている。そして、ある事前分布 w0 に関して、組織設計問題は次のような、二つの分離された別々の異なる局面に分けて考えることができる。
言い換えれば組織構造の設計問題と管理システムの設計問題との分離が可能であることを、この分離定理は述べている。この定理のもつ組織論的に重要な意味は、トップ・リーダーが停止ルール q すなわちサンプリングの決定権を委譲することができるということである。システム2で行われるサンプリングの決定権の委譲は、トップ・リーダーが課業決定問題の最適解であるベイズ最終決定ルール d* を求めるのに、なんら支障をきたすものではない。それ故、この定理は、システム2における観測センターの権限委譲がなんら不利益をもたらさないという意味で、その妥当性を保証するものである。
また、システム2において、観測センターを勤めるあるマネジャーが、観測過程を停止した後、トップ・リーダーのところに組織的観測結果のデータをもってやってくるとしよう。その時、トップ・リーダーは、観測センターがどんな停止ルールに基づいて観測過程を制御してデータを集めたのかを知らなくても、最適な最終決定ルールに到達することの妨げにはならない。§4.3の用語を用いれば、トップ・リーダーは、まるで彼が固定サイズ標本の決定問題に直面しているかのようにふるまい、最適な課業を選ぶのである。
他方、システム1では、トップ・リーダーは定義により観測センターを勤めることになるので、彼は自分自身で組織的観測結果をとるかどうかのサンプリングの決定を逐次方式で行うことになる。したがって、この定理は、経営パターンと意思決定方式(decision procedure)との間の次のような関係を示唆している。
実際、§4.3でも扱われたように、日本企業のケースでは、部門間コンフリクトの解決方法として、「会議」や「根回し」をとる企業では同時方式が多くとられ、「上司」によるコンフリクト解決を行なう企業では逐次方式が多くとられるということがわかっている。この事実発見は、分離定理がその存在を示唆した経営パターンと意思決定方式との間の関係1、2を支持しているのである。
そこで、この分離定理をふまえて、ピラミッド組織でのベイズ・リスクとマトリックス組織でのベイズ・リスクとが比較されることになる。もっとも定理5.1の証明でもわかるように、もしある組織構造において、より小さなベイズ期待損失が達成されるならば、その組織構造は効率的(efficient)となる。組織構造の定義から、もし d*∈D' であるならば、効率的組織構造はピラミッド組織のカテゴリーの中に存在することになり、効率的ピラミッド組織が存在する。このことから、次の定理が証明される。
定理5.2 効率的なピラミッド組織が存在する。
この定理は次の補題からただちに証明できる(Takahashi, 1987)。
補題 Z1=z1, ..., Zj=zj が与えられたときの統計的決定問題には、ベイズ最終純決定関数が存在する。
《証明》 dj*(z1, ..., zj)=( f1*, ..., fm*) とすると、
E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }
=Σi wj(θi| z1, ..., zj) L(θi, dj*(z1, ..., zj))
=Σk fk* Σi wj(θi| z1, ..., zj) L(θi, ak)
いま dj* がベイズ最終決定関数であるならば、任意の ak∈A' について
E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }≦Σi wj(θi| z1, ..., zj) L(θi, ak)
もし仮に、任意の ak∈A' について
E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }<Σi wj(θi| z1, ..., zj) L(θi, ak)
とするならば、
E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }
<Σk fk*Σi wj(θi| z1, ..., zj) L(θi, ak)
=E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }
これは矛盾なので、
E{L(Θ, dj*(z1, ..., zj))| Z1=z1, ..., Zj=zj }=Σi wj(θi| z1, ..., zj) L(θi, ak)
であるような ak∈A' が存在している。すなわち、もし Z1=z1, ..., Zj=zj ならば、そのような ak を選ぶようなベイズ最終純決定関数 dj* が存在する。□
証明からもわかるように、この補題は逐次決定関数に限らず広く一般的に決定問題について成立する。実は、第2章で期待効用原理を考えた際に、意思決定者側の戦略が(混合戦略ではなく)純戦略でのみ考えられていたのだが、これはまったく問題がなかったことになる。自然の状態の集合 Ω 上の確率分布がわかっている場合、この補題が成立するために、混合戦略を考える必要はなかったのである。
ところで、この定理5.2は効率的なマトリックス組織が存在することを否定するものではないが、効率的なマトリックス組織自体が本質的なものではなく、まためったに存在もしないということが次のごく簡単な例によっても示される。
例5.1 例示のために、次のような生産組織をもつ企業を考えてみよう。この企業は互いにかなり離れたいくつかの地域に分散する形で、それぞれ工場と営業所を兼ねた事業所をもち、どこの事業所でも、同じく何種類かの、いずれもかなり特殊な用途の単価の高い製品の製造、販売を行っている。
いまこの企業の組織には2人のマネジャーしかいないとする。マネジャー1は製品別に単位組織の活動をグループ化して、販売員を各製品に専門化させ、製品に精通させることで製品の売り上げ増加を図るなど、売り上げの増加を主目的にした課業を考え、a1 としてトップ・リーダーに進言した。
他方、マネジャー2は地域別に単位組織の活動をグループ化して、製品の部品や組立に要する輸送費を節約するとともに、販売員の移動時間とそれに要する費用を削減することを図るなど、おもに生産・販売コストの低減をねらった課業を考え、a2 としてトップ・リーダーに進言した。
この二つの課業の成果は、製品に対してある程度大きな潜在需要があるかどうかに大きく依存している。もし製品に対する潜在需要が大きければ、マネジャー1の考えた製品別のグループ化は潜在需要を堀り起こすのに大きな効果を挙げるはずであり、マネジャー2の考えた課業では、市場拡大の機会を逃すことになるかもしれない。しかし、もし製品に対する潜在需要がそれほどでなければ、マネジャー1の考えた課業では、販売コスト等の増加を招くだけで、逆に、費用削減をめざしたマネジャー2の課業の方が利益をもたらすことになるはずである。
そこで、製品に対してある程度大きな潜在需要があるような環境の状態を θ1 とし、製品に対してそのような潜在需要がないという環境の状態を θ2 としよう。すると Ω={θ1, θ2}。損失関数はこれまでの話を反映して次のようになっている。
| L(θ1, a1)=0, | L(θ1, a2)=100, |
| L(θ2, a1)=100, | L(θ2, a2)=0. |
| p((1, 1)|θ1)=0.4, | p((2, 2)|θ1)=0.6, |
| p((1, 1)|θ2)=0.6, | p((2, 2)|θ2)=0.4, |
ケースI: 観測センターは組織的観測 z1 を観測した後で、サンプリングを停止したとしよう。すると、トップ・リーダーはこの組織的観測結果 z1 に基づいて統計的決定問題に直面することになる。任意の与えられた事前分布 w0=(w0(θ1), w0(θ2)) に対して、事後分布 w1=(w1(θ1|z1), w1(θ2|z1)) を考えると、損失関数から、課業 a1 をとった場合の事後期待損失は
w1(θ1|z1) L(θ1, a1)+w1(θ2|z1) L(θ2, a1)=100・w1(θ2|z1)
課業 a2 をとった場合の事後期待損失は
w1(θ1|z1) L(θ1, a2)+w1(θ2|z1) L(θ2, a2)=100・w1(θ1|z1)
となる。このことから w1(θ1|z1)+w1(θ2|z1)=1 に注意すると、
したがって、任意の事前分布についてピラミッド組織が効率的となる。もし w=(0.4, 0.6)かつ Z1=(2, 2) ならば、a1 も a2 もともにベイズになる。同様に w=(0.6, 0.4) かつ Z1=(1, 1) ならば、やはり a1 も a2 もともにベイズになる。このように、この二つのケースについてだけ、a1 も a2 の任意の混合がベイズとなり、任意の混合課業のマトリックス組織も効率的となるが、このときもちろんピラミッド組織も効率的なので、本質的なものではない。
ケースII: 観測センターは組織的観測 z1, z2 を観測した後で、サンプリングを停止し、観測結果 z1, z2 をもってトップ・リーダーの所にやって来るとしよう。ケースIと同様の方法で、次のようなベイズ最終決定関数を得る。
したがって、任意の事前分布についてピラミッド組織が効率的となる。次のケースのときだけ、a1 と a2 の任意の混合がベイズとなり、任意の混合課業のマトリックス組織も効率的となる。(1) w=(4/13,9/13) でかつ (Z1, Z2)=((1, 1), (1, 1))。(2) w=(1/2, 1/2) でかつ (Z1, Z2)=((1, 1), (2, 2)) または ((2, 2), (1, 1))。(3) w=(9/13,4/13) でかつ (Z1, Z2)=((2, 2), (2, 2))。
しかしケースIでは、これらの事前確率のときマトリックス組織は効率的ではなかったことに注意してほしい。つまりケースI、ケースIIを通してマトリックス組織が効率的であった事前確率は存在しなかったことになる。したがって、データにかかわらずマトリックス組織が効率的であるような事前分布を特定することはできない。それに対して、管理システムについては、これから見るように、システム1、システム2がそれぞれ効率的であるような事前分布の領域を特定することができる。
次に、効率的管理システムについて考えることにしよう。システム1におけるベイズ・リスクをシステム2におけるベイズ・リスクと比較する。効率的な組織構造のときと同様にして、もしある管理システムにおいて、より小さなベイズ・リスクが達成されるならば、その管理システムは効率的(efficient)であるといわれる。
いま、すべての可能な事前分布からなる集合を
S={w=(w(θ1), ..., w(θs)): Σi w(θi)=1, w(θi)≧0, i=1, ..., s}
とすると、S は s 次元のユークリッド空間において単位ベクトルで張られた (s-1) 次元単体となっている。そこで、システム1におけるベイズ・リスク V1 とシステム2におけるベイズ・リスク V2 を比較してみる。システム1が効率的であるような事前分布の領域は次のように定義される。
S*={w∈S: V1(w)≦V2(w)}
同様に w∈C(S-S*)に対しては、システム2が効率的である。ただし、C(S-S*) は S-S* の閉包を表している。この領域 S* の構造については、次の三つの定理が証明されている (Takahashi, 1987)。
定理5.3 S*=∪j=1m Sj* ただし、Rj(w)=Σi w(θi) L(θi, aj), Sj*={w∈S: Rj(w)≦V2(w)}
定理5.4 いま i 番目の成分が1で、他の成分が0である単位ベクトルを ei=(0, ..., 0, 1, 0, ..., 0) とすると、ei∈S*, i=1, ..., s。また、もし Sr* が空集合でないならば、(1) ei∈Sr* であるような ei が存在し、(2) Sr* は凸集合である。
定理5.5 Sj* は cI、cT、cM に関して非減少である、j=1, ..., m。
このうち、定理5.4はその原型がArrow, Blackwell & Girshick (1949) によって、ごく単純で簡単な逐次決定問題について与えられている。後に、Takahashi (1983)によって、より一般的な逐次決定問題についても成り立つことが証明された。定理5.4で、ei はトップ・リーダーとマネジャーが環境の真の状態が θi であると完全かつ正確に知っているということを意味しているということに注意されたい。したがって、この定理はシステム1が不確実性の存在しない、第2章でいうところの確実性のケースにおいて効率的な管理システムであるということを述べていることになる。しかも、領域 Sj*、j=1, ..., m は、単体 S の少なくとも一つの頂点を含んだ凸集合となる。事前分布は環境の状態に関する不確実性を直接的に表現するものであるから、Sj* は環境に対する不確実性が低いことを表している事前分布の集合である。したがって、システム1は不確実性が低いときに効率的で、システム2は不確実性が高いときに効率的な管理システムである。
また定理5.5から、情報コストが大きくなるにしたがって、システム1が効率的である領域が広くなってくる。不確実性が高ければ、期待損失をより小さくするために、環境の状態の観測をより多く行い、情報の収集を心掛ける必要があり、システム2はまさにこうした状況に適した管理システムであった。ところが、情報コストが上昇してくると、こうした情報収集による環境適応のメリットがコスト的に損なわれてくる。そこでシステム1のような管理システムの方がむしろ効率的となってくるのである。
例5.2 例5.1の問題を続けよう。いま情報コストを cI=3, cT=2, cM=1 とすると、C1(I)=10, C1(S)=0, C2(I)=7, C2(S)=2 となる。Arrow, Blackwell & Girshick (1949)や Blackwell & Girshick (1954)の計算手続きによれば、まず
| 100w(θ1)+9 | if 0≦w(θ1)≦0.4 | |
| inf(q, d) r2(w, (q, d))= | 49 | if 0.4≦w(θ1)≦0.6 |
| 109-100 w(θ1) | if 0.6≦w(θ1)≦1 |
この例のように、自然の状態が二つでも領域 Sj*, j=1, ..., m の計算は一般に繁雑である。自然の状態が三つになると、手計算で行なうのは大変になる。Takahashi (1987)には、そのための計算、作図プログラム TRIGRAPH のリストが掲載されている。
ここまではトップ・リーダーとマネジャーが事前分布をもっていると仮定して議論を進めてきた。第2章の分類に従えば、確実性、リスク、不確実性の三つのカテゴリーのうち、これまでは確実性のケースとリスクのケースについて取り扱ってきたことになる。
第4章の冒頭でも整理したように、不確実性のケースではトップ・リーダーとマネジャーは単に環境のとりうる状態の集合 Ω={θ1, ..., θs} を知っているだけなので、確実性やリスクのケースと比べるとかなり高い不確実性に直面しており、どの意思決定原理をとるのかによって、まったく異なる行動を最良として選択する可能性がある。しかし、意思決定者と自然のゼロ和2人ゲームの均衡点を達成するのは、2人のプレイヤーがワルドのマクシミン原理に則って意思決定を行なった場合だけである。
そこでここでは、マクシミン原理に則って考えることにしよう。つまり、環境の各状態において起こりうる結果のうち組織にとってもっとも悪い結果を考え、そのもっとも悪い結果の中では一番望ましい結果をもたらす決定ルールを選択するということになる。ここでは、このマクシミン原理に則った決定ルールを不確実性のケースでの逐次決定問題の最適ルールと考えて、議論を進めることにしたい。
決定ルール (q0, d0) と管理システム k0 は
supw rk0(w, (q0, d 0))=inf(q, d), k supw rk(w, (q, d))
であるときミニマックス(minimax)であるといわれる。この式の右辺の値はミニマックス・リスク(minimax risk)と呼ばれる。不確実性のケースについては、ミニマックス・リスクを達成する組織構造を効率的といい、同様に、ミニマックス・リスクを達成する管理システムを効率的ということにする。
決定理論の用語法では、
inf(q, d), k rk(w0, (q, d))=supw inf(q, d), k rk(w, (q, d))
であるような分布 w0 は最悪分布(least favorable distribution)と呼ばれる。ここでこの逐次決定問題についてのミニマックス定理が証明される(Takahashi, 1987)。
定理5.6 (ミニマックス定理)
inf(q, d), k supw rk(w, (q, d))=supw inf(q, d), k rk(w, (q, d))
が成り立ち、最悪分布 w0 が存在する。
最悪分布を使うことで、不確実性のケースにおける効率的管理システムと効率的組織構造との間の関係が、次の定理によって証明される(Takahashi, 1987)。
定理5.7 Rj*(w*)=supw minj Rj(w) とすると、(1) w*∈S* ならば、w* は最悪分布である。(2) w*∈S-S* ならば、最悪分布 w0∈C(S-S*)。
ここで w* が、データをとらずに事前分布だけに基づいて決定を行なう、いわゆるノー・データ問題(no data problem)の最悪分布であるということに注意されたい。この定理の (1)のケースでは、最悪分布 w* は S* に属しているので、システム1が効率的管理システムである。その上、Rj*(w*)=supw minj Rj(w) を満たすという w* の定義から、課業 aj*∈A' が選ばれることがわかる。つまりマネジャー j* がライン権限をもち、他のマネジャーはトップ・リーダーのスタッフとなって、ピラミッド組織が効率的組織構造となる。(2)のケースでは、最悪分布が C(S-S*) に属しているので、システム2が効率的管理システムである。しかし、どちらの組織構造が効率的かは一般的にはいえない。以上のことから、この定理5.7は次のような効率的管理システムと効率的組織構造との間の関係を示していることになる: 厳密な不確実性のケースでは、もしシステム1が効率的であれば、ピラミッド組織も効率的である。
例5.3 例5.2の問題をさらに続けよう。トップ・リーダーは今度はワルドのマクシミン原理に則ってミニマックス決定関数をとると考える。定義から、w*=(0.5, 0.5) で、例5.2の S* から w*∈S-S* であることがわかる。したがって定理5.9 (2)から、最悪分布 w0∈C(S-S*) となるはずである。実際、例5.2の結果から
| 100w(θ1) | if 0≦w(θ1)≦0.49 | |
| inf(q, d), k rk(w, (q, d))= | 49 | if 0.49≦w(θ1)≦0.51 |
| 100-100 w(θ1) | if 0.51≦w(θ1)≦1 |
ここで、これまでに得られた結果を効率的組織形態に関する命題にいい直すことにする。定理5.2、定理5.4はそれぞれ次のように言い換えることができる。
命題5.1 もし組織が、確実性のケースかリスクのケースに直面しているならば、ピラミッド組織が効率的である。
命題5.2 もし組織が確実性のケースに直面しているのであれば、システム1が効率的である。もしリスクのケースに直面しているのであれば、システム1はより低い不確実性の下で効率的であり、システム2はより高い不確実性の下で効率的である。
これらの命題は、コンティンジェンシー理論で主張されている、環境の不確実性とそれに適した組織形態との関係を部分的に支持するものである。
命題5.1は、マトリックス組織が効率的でありうるのは組織が厳密な不確実性のケースに直面しているときだけであることを示唆しているので、マトリックス組織が望ましいとされる必要条件は不確実性が高いことであるという Davis & Lawrence (1977) の主張を支持している。
命題5.2は、Burns & Stalker (1961) の主張の一部を支持していると考えられる。管理システムの定義から、システム1ではトップ・リーダーがマネジャーの観測活動を調整し、環境についての情報を、垂直的な伝達経路を通して集め集中的にもつことになる。それに対して、システム2では、マネジャー間のネットワークの中でその時々の観測センターがマネジャーの観測活動を調整するので、環境についての情報はネットワークの中での水平的な伝達経路を通して、ネットワークのどこかに位置することになる。こうしたシステム1、システム2の特徴は、それぞれ Burns & Stalker の機械的システム、有機的システムの伝達・調整面の特徴と同じものである。したがって、命題5.2は Burns & Stalker の効率的管理システムについての主張を伝達・調整面に関して支持している。
また、定理5.7で示されているように、厳密な不確実性のケースでは、ワルドのマクシミン原理に則れば、システム1が効率的なときにはピラミッド組織も効率的である。したがって、命題5.1、命題5.2の確実性、リスクのケースも含めて、次に述べるような関係が得られる。
命題5.3 確実性、リスク、厳密な不確実性のどのケースでも、システム1が効率的であるならば、ピラミッド組織も効率的である。
以上のような効率的組織構造、効率的管理システムに関して得られた命題の妥当性については、§4.3でも触れている調査データを用いた検証が試みられ、Takahashi (1987, ch.6; 1988)にそれぞれその一部が発表されている。ここで詳述することはできないので、簡単に結論部分だけを整理すると以下の通りになる。
まず、組織や意思決定者が実際に直面している不確実性の程度を、確実性、リスク、厳密な不確実性のケースに分類する客観的な方法がないので、検証可能なように、命題5.1~5.3からそれぞれ次のような仮説を導いておく。
仮説5.1 低業績のピラミッド組織と高業績のマトリックス組織は、高業績のピラミッド組織と低業績のマトリックス組織に比べると、より高い不確実性に直面している。
仮説5.2 低業績のシステム1と高業績のシステム2は、高業績のシステム1と低業績のシステム2に比べると、より高い不確実性に直面している。
仮説5.3 高業績のシステム1採用組織はピラミッド組織を採用している。
高業績・低業績の分類は企業の自己評価に基づいて行ったが、成長率や各種経営指標といった客観指標によってこの分類の妥当性が確認されている。また不確実性については、直接測定する方法がないので、仮説5.1、仮説5.2については製造業に限定して調べることにし、生産設備・装置の更新サイクル、主要製品のライフ・サイクルを最近のケースについて年数で答えてもらったものを利用した。生産設備・装置の更新サイクルが短ければ、生産ラインが管理状態に到達するまで一定の時間を要するので、その分高い不確実性に直面することになるし、主要製品のライフ・サイクルが短ければ、それだけ頻繁に新しい市場に対処することになり、やはり不確実性が高くなる。したがって、どちらも値が小さくサイクルが短いほど高い不確実性に直面していることを示していると考えられる。
調査データは三つの仮説を支持している。仮説5.1については組織構造と業績の二元配置の分散分析、仮説5.2については管理システムと業績の二元配置の分散分析を行い、仮説にある関係が確認された。仮説5.3については、高業績企業について組織構造と管理システムのクロス集計表をつくることによって、やはりその関連が確認されている。
組織活性化とは何かということについては、この章の最後に議論することにして、ここではとりあえず、Takahashi (1992a)にしたがって、活性化された状態とは、「組織のメンバーが (1)組織と共有している目的・価値を (2)能動的に実現していこうとする状態」ではないかと考えることにしよう。組織の活性化された状態をこのように定義しようという基本的なアイデアは、前章の数理的な組織設計論から得られたものである。
前章では、課業の選択過程が逐次決定問題として定式化されるような組織についての組織設計問題を経営学及び経営組織論の概念的枠組みに基づいて考察した。組織形態は組織構造と管理システムとの組で表現され、課業の逐次決定モデルの一部を構成することになる。システム1、システム2の2タイプの管理システムは環境の観測過程における伝達システムとして定義され、ピラミッド組織、マトリックス組織の2タイプの組織構造は課業の割り当てシステムとして定義された。したがって、組織形態は、組織構造と管理システムによる表6.1のような組で表現される。この四つの組織形態のうち、どの組織形態が効率的かということを分析してみたわけである。
表6.1 組織形態
| 組織構造 | 管理システム | |
|---|---|---|
| システム1 | システム2 | |
| ピラミッド組織 | P1 | P2 |
| マトリックス組織 | M1 | M2 |
ところで、以上の理論的考察は、ある仮定の上に成り立っているが、それらのうち基本的なものは、第5章の仮定5.1と仮定5.2である。このうち仮定5.2については、厳密な不確実性のケースにも配慮した表現にして、ここに二つの仮定を再掲しておこう。
基本的仮定6.1 各マネジャーはある組織的活動をトップ・リーダーに推薦する。
基本的仮定6.2 トップ・リーダーとマネジャーは同じ損失関数をもっている。また環境の状態について主観確率分布をもつならば、それらは同じ確率分布である。
基本的仮定6.2は「マネジメント・チームの存在」と呼ぶこともできる。ここで、マネジメント・チームとは同じ損失関数、同じ確率分布を共有するトップ・リーダーとマネジャーのグループのことである。「チーム」という名称はそれが Marschak & Radner (1972) のチームの定義を満たしていることからつけられた。
この二つの仮定は、実際の日本企業の調査研究が進むにしたがって、組織設計の制約条件として実際的に意味をもつものであることが、しだいに明らかになってきた。既に、数理的な組織設計論の結果として示されたように、効率的組織形態は環境、特に環境の不確実性に依存している。しかし、こうした組織設計問題に対する解答は、二つの基本的仮定の下でのみ意味をもっている。そこで、この二つの基本的仮定を満たす組織を、コンティンジェンシー理論が成立し得る組織、そして環境の不確実性に応じて組織形態を選択し得る組織という意味で、コンティンジェンシー組織(contingency organization)と呼ぶことにしよう。つまり、コンティンジェンシー組織は表6.1のすべての組み合せ、P1、P2、M1、M2の組織形態をとることができるので、組織設計問題の解が得られれば、どのような解であっても、それを適応可能な組織ということができる。
もし、組織が基本的仮定6.1を満たさないのであれば、マトリックス組織を選択できる機会が失われ、組織はピラミッド組織をとるしかなくなる。つまり、表6.1でいうと、ピラミッド組織の横の行であるP1、P2だけが、とりうる組織形態となる。
もし、組織が基本的仮定6.2を満たさないのであれば、第5章の定理5.1が成立しなくなり、サンプリング決定の権限をマネジャーの誰かに委譲することができなくなるので、組織はシステム2を選択できる機会を失う。すなわち、システム1をとるしかなくなる。したがって、表6.1でいうと、システム1の縦の列であるP1、M1だけが、とりうる組織形態となる。
もし基本的仮定6.1と6.2のどちらも満たされないのであれば、組織は組織構造としてはピラミッド組織、管理システムとしてはシステム1をとるしかなくなる。つまり、表6.1でいうと、可能な四つの組み合せのうち、わずかに一つP1だけが、とりうる組織形態となる。このような組織は官僚制組織と呼ばれ、古典的な経営組織論の世界では唯一の組織モデルであった。言い換えると、コンティンジェンシー組織であることは、官僚制組織と比べ、トップ・リーダーにとっての選択の機会を拡大することを意味し、マトリックス組織とシステム2はコンティンジェンシー組織の中においてのみ許される代替的組織形態なのである。このように、コンティンジェンシー組織はそうでない組織に比べて、適当な組織形態を選択できる可能性が大きいので、効率的組織構造や効率的管理システムが環境の不確実性に依存していたとしても、「効率的」な組織であるということができる。コンティンジェンシー理論が主張するように、組織化に唯一最善の方法は存在しないが、トップ・リーダーが最善の組織化の方法を選ぶことを可能にするような組織の類は存在する。それがコンティンジェンシー組織なのである。
そして、このコンティンジェンシー組織が満たすべき条件である二つの基本的仮定6.2、6.1に対応する形で、先程の組織の活性化された状態の定義である「組織のメンバーが (1)組織と共有している目的・価値を (2)能動的に実現していこうとする状態」が考え出された。したがって、組織がコンティンジェンシー組織となり、数理的な組織設計論によって示されているように「効率的」な組織となることを組織の活性化と考えたのである。このことの是非は§6.3で詳しく検討される。
そこで、まず組織の活性化された状態の定義「組織のメンバーが (1)組織と共有している目的・価値を (2)能動的に実現していこうとする状態」のうち、(1)の組織と目的・価値を共有している程度を表すものとして一体化度指数を、(2)能動的に思考している程度に関連して無関心度指数を設定しよう。その上で、この二つの指数を用いた組織の活性化分析の手法としてI I図法(I-I chart method)を取り上げる。I I図が組織の活性化分析に有用であることを確認するために、I I図が当然持つべき性質を仮説として設定するが、検証は次節以降に回す。
第4章でも述べた通り、各々の組織メンバーには、代替案レベルでは「無関心圏」が存在し、その圏内にある代替案は意識的に反問することなく受容しうるのだと考えられる。命令を受けた者は無関心圏内にある代替案に対しては、その内容が何であるのかについて比較的無関心に、命令を受け入れるのである。
無関心圏が大きいということは、上司の命令に対して忠実で従順であることを意味しているのだが、反面、受動的で、組織の中で受け身でいることも意味している。いわれたことは実行するが、自分で代替案をつくっていくようなことはしない。前述の基本的仮定6.2が求めているような、部下が活動計画案を自分で立案し、上司に進言するということは起こりにくいのである。
逆に、無関心圏が小さければ、少なくてもトップ・ダウン型の意思決定は行いにくくなる。部下は無関心圏が小さくなった分だけ、より頻繁に命令の内容を意識的に反問した上で、受容するかどうかを決めるので、上司にとっては忠実で従順な部下という感じではなくなるのである。しかし、命令内容が反問されることで、そして、おそらくボトム・アップ型に部下から命令内容とは異なる独自の活動計画案が進言されてくることで、命令の内容に部下の意見が反映されていくことになる。
また無関心圏は、上司から部下への命令という「下へ」の局面だけではなく、「上へ」の局面にも、「横へ」の局面にも当てはまるのだが (Simon 1976, p.12 邦訳p.15)、こうした組織内での相互関係を考えてくると、無関心圏の大きなメンバーは組織の中では、一般的に素直で、従順であるということができる。すなわち、無関心圏が大きいということは、そのメンバーが単に上司に対して忠実だということだけではなく、あらゆるメンバーに対してのそのメンバーの従順さ、素直さを表しているともいえる。
こうして無関心圏の大きさは、受動的か能動的かといったメンバーの特性にかかわってくることになる。そこで、無関心圏の大きさを表す指数として無関心度指数(indifference index)を考えた。すなわち、組織メンバーの課業・処遇等に本質的に重大な影響を及ぼすはずの経営諸施策等に対して、どの程度まで無関心でいられるのかをこの指数で表した(実際の算出方法については章末付録を参照のこと)。
第4章でも述べたように、メンバーが意思決定を行うにあたって、一定のグループにとっての結果の観点から、いくつかの代替案を評価するとき、その現象を一体化と呼ぶ。すなわち、メンバーが、組織と目的・価値を共有しているとき、そのメンバーは、組織に自身を一体化していると呼ぶのである。
そこで、一体化の程度を表す指数として一体化度指数(identification index)を考えた。無関心度指数のときと同様に、組織メンバーの課業・処遇等に重大な影響を及ぼすはずの経営諸施策等に対して、個人の立場からの評価と、会社の立場からの評価がどの程度一致しているのかをこの指数で表した(実際の算出方法については章末付録を参照のこと)。
一体化の意味は、無関心圏に比べるとはるかに明らかであろう。ただし、ここで注意が必要なのは、組織全体ではなく、その下位グループに一体化している場合である。実は、ここでの一体化度指数は、会社全体に対する一体化を考えているので、下位グループに対する一体化は、反映されない可能性がある。というより、組織全体の目的・価値と下位グループの目的・価値が一致していないとき、すなわち、セクショナリズムの傾向が強いような時には、一体化度指数は低くなるだろう。したがって、ある企業の一体化度指数が高いときには、全社一枚岩であることを意味しているが、一体化度指数が低いときには、メンバーの目的・価値の共有の程度が低いか、または共有しているのは下位グループの目的・価値で、セクショナリズムが蔓延っているような状態であることを意味していると考えられる。
無関心度指数を横軸、一体化度指数を縦軸にとったグラフはI I図 (I-I chart; Identification-Indifference chart) と呼ばれる(Takahashi, 1992a)。前述の無関心度指数と一体化度指数のもつ意味から、I I図によってメンバーの特徴づけを行うことができる。無関心度指数の高低と一体化度指数の高低の組み合わせから、図6.1のように四つのタイプに類型化して考えることができる。
図6.1 I I図によるメンバーの類型化
また、先程の組織の活性化された状態の定義である「組織のメンバーが (1)組織と共有している目的・価値を (2)能動的に実現していこうとする状態」にしたがえば、無関心度指数が低く、一体化度指数の高いタイプ3のメンバーが多ければ、組織は活性化された状態にあるということができる。
ただし、ここで注意が必要なのは、この研究ではこうした類型化を行うことで、4タイプの間に境界線を引くことを考えてはいないということである。その意味で、I I図はメンバー特性の判別のための図ではない。問題となっているのは、相対的な位置である。例えば、無関心度指数が高く、一体化度指数が低いメンバーと、それに比べて、無関心度指数が低く、一体化度指数が高いメンバーとを比較すれば、前者の方が、より疎外労働者的であり、後者の方が、より問題解決者的であるということであり、指数の上での差が大きければ大きいほど、その特徴が強く現れてくるだろうということである。
また、以上のような考察は、次のような推測を可能にしてくれる。すなわち、タイプ4は非貢献者型であり、実際には、このタイプのメンバーの多い組織は組織的行動がとれずに、存続が難しくなる。それ以前の問題として、そのような傾向をもった者をメンバーとして企業が受け入れるとは考えにくい。したがって、仮に、無関心度指数と一体化度指数が正しく測定されているとすると、次のような仮説を立てることができる。
仮説6.1 無関心度指数も一体化度指数も共に低いようなタイプ4の者は、実際の企業の組織には少ない。
March & Simon (1958, pp.6-7 邦訳pp.10-11) はそれまでの組織についての命題は、人間の諸属性のうちのどれを考慮に入れるべきかということについての一連の仮定が明示的にもしくは暗黙のうちに前提として含まれていると主張した。そして、組織内行動についての諸命題をその仮定によって次の三つに大分類した。
この三つの分類はここでのタイプ1、2、3にほぼ対応している。タイプ4は仮説6.1が正しければ、現実にはほとんど見られないはずで、彼らも考えていない。彼らは「これら3組の仮定は、相互になんら矛盾するものではない。人間というものは、これらの側面のすべて、おそらくはそれ以外の側面をも、もっているであろう。」(March & Simon, 1958, p.6 邦訳p.10)と述べている。しかしむしろ、個々の人間レベルでは3組の仮定のいずれかによく当てはまるケースの方が多いだろう。つまり、タイプの異なる個人が存在し、タイプが異なる以上、各人に適用可能な理論も異なってくると考えた方が自然だろう。
いま、タイプ1のメンバーを中心とした組織をタイプ1の組織、同様にタイプ2、タイプ3のメンバーを中心とした組織を、それぞれタイプ2の組織、タイプ3の組織と呼ぶことにしよう。仮説6.1から、タイプ4の組織は考えないことにする。そこで、この3タイプの組織が持っているはずの組織特性について考えてみよう。
前節の議論から、タイプ1、タイプ2の2タイプは無関心度指数が高いタイプなので、本的仮定6.2を満たさず、マトリックス組織をとることができない。したがって、とりうる組織構造はピラミッド組織のみということになる。
さらに、同じピラミッド組織であっても、タイプ1の組織は無関心度指数が高く、メンバーがトップの命令、指示に従順で素直というだけでなく、一体化度指数も高いため、セクショナリズムもなく、全社一丸となって、目標、仕事に当たるような組織である。
それに対して、タイプ2の組織は無関心度指数が高く、メンバーはトップの言ったことは真面目に、かつ忠実に実行するが、一体化度指数が低く、組織の目的・価値と個人の目的・価値との間に一線を画するために、全社一丸となることはなく、メンバーはどこか覚めた目で、ビジネスライクに組織の仕事を行い、官僚的、役人的になり、組織もお役所的な感じになっていると考えられる。あるいは、そこまでいかなくても、セクショナリズムの傾向が強いかもしれない。前節で、基本的仮定6.1、6.2のどちらも満たさない組織は官僚制組織となると述べたが、タイプ2のメンバーが中心のタイプ2の組織は、この基本的仮定6.1、6.2のどちらも満たさない組織であり、まさしく官僚的、役人的組織となる。
タイプ3の組織は前節の基本的仮定6.1、6.2を満たすような組織、つまりコンティンジェンシー組織である。ということは、タイプ3の組織においてのみマトリックス組織およびシステム2の両方を選択することができるので、マトリックス組織でかつシステム2をとっている組織はタイプ3の組織と類別してかまわないはずだ。特に、マトリックス組織をとりうる、基本的仮定6.2を満たすような無関心度指数が低い2タイプのうち、タイプ4は存在しないと考えられるので(仮説6.1)、マトリックス組織をとっている組織があれば、タイプ3の組織に類別できる。
以上のことをまとめると、実際の組織をその組織特性から予想して「タイプ1・2・3」に分類するときのポイントは次のようになる。
ここで、「 」は予想される組織特性のタイプであることを示している。もし無関心度指数と一体化度指数が正しく測定されているならば、次の仮説にあるような関係が見いだされるはずである。
仮説6.2 「タイプ1・2・3」に予想類別された組織の間には、I I図上で図6.1で示されたような位置関係がある。
仮説6.1とともにこの仮説6.2が検証されると、無関心度指数と一体化度指数は正しく測定されているということが確認できる。
既に述べたように、組織の活性化された状態の定義である「組織のメンバーが (1)組織と共有している目的・価値を (2)能動的に実現していこうとする状態」に従えば、無関心度指数が低く、一体化度指数の高いタイプ3のメンバーが中心のタイプ3の組織は、活性化された状態にある組織、すなわち、活性化組織である。
仮説6.1、6.2を検証するために、調査が実施された。対象となったのは日本生産性本部の経営アカデミー『人間能力と組織開発』コースの参加者の所属企業7社である。調査は2段階に分けて行われた。第1段階として、1986年6月14・15の両日に、合宿形式で各社1人ずつ7人と筆者の計8人からなるグループで相互のヒアリングを行った。この段階では、各社の会社概要、トップの経営方針、組織的特徴、社風などを中心に1社平均100分程度をかけて、報告、質疑応答等の議論を行い、各社の特性を浮き彫りにする作業が行われた。
調査の第2段階は、各社での標本調査であった。当初、企業間の違いと同様に、年齢別階層間での違いも大きくなると予想されたこともあり、標本の選び方は企業間での企業特性の比較が可能になるように、まず各社において、ヒアリングの対象者を含んだ人員規模が200人から400人程度のホワイトカラーの組織単位を選び、さらにその中から、年齢別階層でみた分布がなるべく均等になるように、各社50人から60人程度を抽出した。その上で、1986年9月3日(水)に各社一斉に、質問調査票を標本に選ばれた人、7社合計で385人に配布し、記入してもらった上で、匿名性を守るために、封筒に入れたものを9月8日(月)までに回収するという形で標本調査が行われた。回収された調査票はあらかじめ決められた指示にしたがって、各社の担当者によって点検された上で、筆者がクリーニングを行った。その結果、374人から質問調査票が回収できた。回収率は97.1%であった。このうち、無関心度指数と一体化度指数を算出するのに必要な項目にすべて回答している331人 (配布人数385人の86.0%)が、ここでの分析対象になった。
実際に331人を一体化度指数と無関心度指数とでI I図上にプロットすると、図6.2のような散布図が得られる。
図6.2 I I図によるメンバーの散布図(N=331)
Cramer's V=0.252 (χ2=104.960***)
Kendall's τb=-0.257***
Pearson's r=-0.351***
(+ p <0.1; * p <0.05; ** p <0.01; *** p <0.001)
この散布図をみると、無関心度指数と一体化度指数がともに小さいような人が少なかったことがわかる。つまりタイプ4の非構成員型の組織メンバーは少なく、仮説6.1の関係が確認された。
仮説6.2の検証のためには、I I図で位置関係を確認する前に、各社の組織特性をあらかじめ予想して、「タイプ1・2・3」に分類しておく必要がある。調査の第1段階での調査結果をふまえて、ここでは次のように7社を類別した。
A社は、1970年に日本の自動車メーカー2社、米国の自動車メーカー1社の共同出資により、自動車部品メーカーとして設立されたまだ若い会社である。1981年からは米国の自動車メーカーが株式を他の2社に売却し、現在は日本の自動車メーカー2社が株式の65%と35%をそれぞれもち、取締役は両社のOBがなり、設立からの日が浅いので、部長も両社の出向で占められている。親会社が今までのところ好調であるために、従業員は親方日の丸的にやってきている。その分、従業員は素直で、トップの言うことに従順で、目標が与えられると、全社一丸となりやすい。組織の面でもセクショナリズムはみられず、一枚岩となっている。実際、1984年から1985年にかけての経営効率化プログラムでは、全社挙げての推進が功を奏し、間接部門では一人当たり20%程度の時間の効率化を達成しているが、さらに良い例が、調査時点で進行中だった間接部門を中心とした人件費削減をめざした経営の効率化である。これは超過勤務手当の大幅カットなどによるコスト・ダウンを含めたかなりの荒療治でありながら、社員の協力を得て、きちんと実行され、目標を達成している。以上からA社はメンバーが従順でセクショナリズムもなく、典型的な「タイプ1」の組織だといえる。
B社はある電力会社の自家用電球製造工場として子会社でスタートし、現在でも株式の46.9%はその電力会社がもっている。社長、そして取締役の半分はその電力会社からきているが、取締役の残りは生え抜きになっている。B社もA社同様、社員は素直で従順である。例えば、1984年に現在の社長が就任し、経営計画を実行に移したとたん、全社的な推進により、年率10数%の売上高の伸びを記録している。また、セクショナリズムもあまりないので、「タイプ1」の組織だといえる。
A社、B社はともに子会社であるという共通点をもつが、これは両社が親方日の丸的で受動的な特徴をもつに至った主因と考えられる。
C社は石油精製工場を子会社の形でもっているが、厳密には石油販売の商社である。顕著な特徴は、総務部、勤労部、経理部、運輸部などの各部門に所属したままで、全国各地の事業所の間を転勤することが頻繁に行われているが、部門間でのジョブ・ローテーションはなく、各部門の長は常務の担当制になっているなど、縦の締め付けが強く、セクショナリズムの傾向が現れていることである。したがって「タイプ2」の組織と考えられる。
D社は調査の前年までは、文字通りお役所の一つだったところである。従来は職能別ライン統制型組織であり、全国に展開する局の局長がアパート、マンションの管理人にたとえられ、局は独立した職能別単位が同居しているにすぎなかった。そのため、縄のれんと言われるほど職能別セクショナリズムが顕著であった。民営化により、サービス別・商品別の事業部制を導入したりしているが、いまでも、上から言われれば、皆本気でやるが、自分で自分の仕事を作っていく力が弱いというトップの発言にみられるように、民営化前の特性をひきずってきている。D社ではメンバーは上から言われることに従順ではあるが、セクショナリズムがあり、「タイプ2」の組織である。
E社は大手の百貨店である。全社的にマトリックス的な組織運営を行っている。例えば、部門間の横断的なプロジェクト・チーム、タスク・フォースの編成を行うことで、水平的なネットワークの形成をめざしている。さらに、人件費を抑制するために人材の積極的な再配置を推進し、本社員からパート、アルバイト、派遣社員といった準社員へ、あるいは準社員から本社員へと相互に雇用形態の転換を図る制度(圧倒的に前者の方が多いが)や、さらには店舗から本部、事業部への人材再配置など人事面での流動化を積極的に進めている。また仕事は職務にではなく人についているものだとの考え方もなされている。つまり、仕事は組織でするというより、むしろ人が行うもので、その人が集まって組織となっていると考えるのである。以上からE社は「タイプ3」の組織に近いものであるといってよいだろう。
F社は都市銀行である。全社的にマトリックス組織になっている。具体的には、次の2レベルで、多元的命令系統をとっている。(i)本部組織である各部門(大きくは、企画本部、業務本部、国際本部、関連事業室、事業調査室、人事部、検査部、総務部、資金証券部)は各支店に対して、それぞれ別個に命令・指示を与えている。(ii)平均的な大きさの各支店内部には、出納、融資、窓口、渉外にそれぞれ2名程度、合計で8名前後の支店長代理がいて、各支店長代理の指示のもとに、実際の業務担当者が働くことになるが、例えば融資担当の支店長代理は2名いるので、この段階で融資の業務担当者は上司を2名もつことになる。その上、ある仕事が忙しくなれば、少しでも手のあいている人は、本来の自分の仕事ではなくても、手を貸すことになる。したがって、実際の業務担当者は8人の支店長代理の下で流動的に運用されていることになる。以上からF社は「タイプ3」の組織である。
G社は大手の電機メーカーである。G社では社内で部門間のコミュニケーションを促進するために、各種委員会やプロジェクト・チームを編成することもしているが、なんといってもこの会社の大きな特徴は、組織面での大きな流動性である。技術系の人間が営業に回ったりという組織の壁を超えた部門間の人事異動が積極的に行われているだけではなく、例えば「人事課」のような職能名をつけた課はほとんどなく、「○○課長のグループ」が存在し、そのグループが人事の仕事をすることになる。ただし、各グループ内で命令系統は一元的である。こうした組織のねらいは、個々のメンバーを特定の細分化された業務の担当としていちいち任命するのではなく、各グループ内で人手が必要となった業務に逐次流動的に割り当てていこうということにある。したがって、仕事の内容や量が変わっても、組織をいちいちいじらずに、人材を流動的に運用することで対処しようというのである。これはまさにマトリックス組織の発想であり、以上からG社は「タイプ3」の組織である。
以上のような類別化をもとにして、各社について無関心度指数と一体化度指数の平均値をとると、表6.2のようになる。各社の無関心度指数の平均値の間、および一体化度指数の平均値の間には有意な差がみられた。
表6.2 7社の無関心度指数と一体化度指数の平均値
| A社 | B社 | C社 | D社 | E社 | F社 | G社 | 全体 | F | |
|---|---|---|---|---|---|---|---|---|---|
| 無関心度指数 | 3.76 | 3.47 | 3.89 | 3.31 | 3.15 | 3.06 | 2.96 | 3.36 | 3.61** |
| 一体化度指数 | 3.68 | 3.74 | 2.82 | 2.81 | 3.26 | 3.41 | 3.29 | 3.30 | 4.23*** |
この平均値により各社をI I図上にプロットしてみると図6.3が得られる。この図から、仮説6.2の関係が確認できる。「タイプ1・2・3」の組織は予想されたような相対的位置関係でI I図上に位置している。またこのことは、マトリックス組織はI I図上でタイプ3の組織においてのみとりうる組織構造であるという数理的組織設計論から導出された関係も支持しているので、数理的組織設計論の結論の傍証ともなっている。
図6.3 I I図による6社の特性比較
仮説6.1、6.2の検証の他に、今回の調査結果からは、次のような興味深い事実発見が得られた。
表6.3 職種ごと、職位ごとの無関心度指数と一体化度指数の平均値
| 職種 | 職位 | |||||||
|---|---|---|---|---|---|---|---|---|
| 営業 | 事務 | 技術 | F | 部課長 | 係長・主任 | 一般 | F | |
| 無関心度指数 | 2.96 | 3.44 | 3.45 | 3.11* | 2.90 | 3.45 | 3.51 | 5.81** |
| 一体化度指数 | 3.48 | 3.18 | 3.52 | 2.58+ | 3.61 | 3.13 | 3.26 | 3.33* |
一つは、営業、技術、事務といったおおまかな職種でみたときの、メンバー特性についての事実発見である。図6.4は職種ごとの一体化度指数と無関心度指数の平均をI I図上に示したものであるが、図6.1のI I図によるメンバーの類型化を参照すると、次の事実発見が得られる。
事実発見6.1 営業職はタイプ3の問題解決者型で活性化されていて、事務職はタイプ2の疎外労働者型、技術職はタイプ1の受動的器械型である。
これは通常抱かれているイメージと合致したものになっている。事務職が官僚的なのは「官僚」という言葉の通りといっていい。営業職については、環境との境界にあって、組織と目的・価値を共有しつつ、それを文字通り積極的に実現することを、言い換えれば、活性化された状態にあることを、常に求められているわけであって、個々の営業マンはある程度自律的な問題解決者として機能することを日常的に要求されている。このことを考えると、この事実発見は納得できるとともに、組織の活性化のための一つの方策を示唆している。すなわち、組織活性化のためには、技術職、事務職といえども、できるだけ営業的な業務を入れて、それにつかせるべきであるということである。
図6.4 I I図による職種の比較
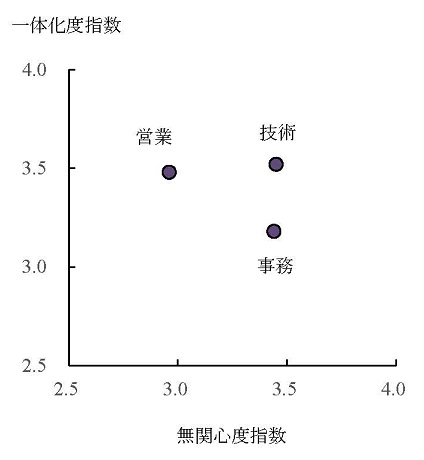
もう一つの事実発見は職位に関係するものだが、図6.5にみられるように、部課長クラス、係長・主任クラス、一般とおおまかに職位に分けて、職位ごとに一体化度指数と無関心度指数の平均を求めて、I I図上に示すと、次の事実発見が得られる。
事実発見6.2 部課長クラスはタイプ3の問題解決者型で、一般、係長・主任クラスと比べて、活性化している。
この事実発見6.2はごく当たり前で、説明の必要もないと思われる。裏を返せば、I I図が組織の活性化分析に有用であることの一つの傍証となりうる。
図6.5 I I図による職位の比較
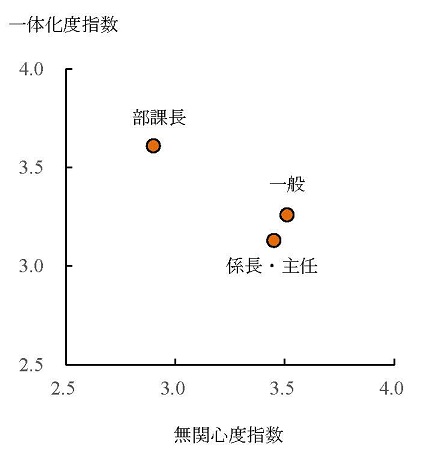
以上のような考察をふまえて、この章の冒頭で宿題として残しておいた組織活性化とは何かということについて考えてみることにしよう。
「組織活性化」はもともと外来語ではなく、英語の原語も存在しないらしい。これまで日本語に翻訳されている経営書などで「活性化」という訳語を見つけると、できるだけその原典に当り、その原語が何であったのか確認する作業を続けてきたが、これまでのところ、何か特定の用語の定訳というわけではないらしいことがわかってきた。代表的なものとしては、mobilization、utilization、revitalization、energization などの訳語として「活性化」が用いられることがあるが、いずれも人的資源等の有効利活用や産業再活性化などの意味で用いられるもので、組織の活性化とはややニュアンスが異なる。日本で使われている「活性化」は、欧米から導入されたというよりは、むしろ国内で独自に使われ始めたもののようである。
実際、「組織活性化」という用語は、1970年代半ば頃からしばしば用いられるようになったが、主に組織開発の分野で日本にある考え方や技法などをすべて包括しているあいまいな概念であるといわれる(馬場, 1989)。その意味では、組織活性化は国産の経営学のテーマなのである。最近になって、Takahashi (1992a)やKawai (1992)が「組織活性化」の英訳として、"organizational activation" という用語を当て、欧米の学術誌に掲載している。活性化に "activation" の英訳をつけ、逆に欧米に輸出しようというわけだが、筆者としては、これが定着することを願うのみである。
このように「組織活性化」が国産の経営学テーマであったという事情にもよるのだろうが、組織活性化をめぐる本当の問題は、その英訳が定まらないという表面的なことではなく、実はその定義自体がきわめてあいまいだということにある。
実際、活性化にしろ活力にしろ、ひろく使われている用語にもかかわらず、企業や組織に関して用いられる場合には、必ずしもその真意は明確ではない。例えば、通産省産業政策局 (1984) のレポートでは「活力ある企業活動」を「企業が市場ニーズに対応して、新製品の開発、製品の高品質・低価格・早納期を積極的に実現していくこと」と定義している (p.6)。こうして定義すると、これはコンティンジェンシー理論にみられる環境適応のアイデア(例えば、Lawrence & Lorsch (1967))と似ているようにも見える。
しかし、活性化の場合には、コンティンジェンシー理論のように、環境の様々な状態に対して、「それぞれの状態に適した組織の活性化」が考えられているわけではない。一般には、環境の状態が等しければ、より高い業績を挙げる組織の状態が普遍的に存在することを想定し、その状態を「活性化された状態」と考えているのである。すなわち、活性化された状態とは環境の状態にかかわらず、良い状態であり、環境の状態との組み合わせで善し悪しが決まるという性質のものではない。
そこで、本書では、組織の活性化された状態(activated state)の定義として「組織のメンバーが、(1)相互に意思を伝達し合いながら、(2)組織と共有している目的・価値を、(3)能動的に実現していこうとする状態」を提案することにしたい。この定義は既にこの章の中で行なってきた定義(2)(3)に(1)を付け加えたものであるが、こうすることで、組織の活性化された状態は、Barnard (1938, p.82 邦訳p.85)の組織成立の必要十分条件「組織は、(1)相互に意思を伝達できる人々がおり、(2)それらの人々は行為を貢献しようとする意欲をもって、(3)共通目的の達成をめざすときに成立する。」とも基本的に合致することになる。そして、組織の活性化された状態の定義(1)(2)(3)に基づいて組織活性化を議論することは、今日におけるBarnard組織論の実践的再評価を意味することになるのである。
『広辞苑 第三版』(岩波書店)によると、「活性化」とは「沈滞していた機能が活発に働くようになること。また、そのようにすること。」とあるが、沈滞していた組織、というより、既に組織として機能しているかどうかも疑わしくなった「組織」をBarnardの組織成立の必要十分条件を満たすような状態にすることを「活性化」であると考えると、活性化の議論は組織論的にすっきりすることになる。
実際、組織論研究者が、身の回りの日本企業や組織から持ち込まれる課題、つまり解明すべき組織現象は、その多くが病理的現象である。つまり、Barnardの組織成立の必要十分条件を満たすような組織本来の姿ではなく、そこから逸脱した状態が問題となって、研究課題として持ち込まれるのである。したがって、本書の提案する組織の活性化された状態の定義は、組織の病理現象を扱うという問題領域の設定の観点からは都合がよい。この定義を受け入れるならば、こうして持ち込まれる研究課題は,すべて組織活性化を目的として持ち込まれていることになる。日本の企業や組織が抱える問題に研究者が目を向け、研究上のイシューとして認知する限り、「組織活性化」は組織の病理現象を扱う問題領域として存在することになる。
ところで、もともと多様なイメージをもたれている活性化をこのように定義してしまうことに、反発を感じる読者もいるだろう。そこで、ここで提案されたような組織の活性化された状態の定義が、一般にもたれている「活性化」のイメージとどの程度重なるものであるのかを簡単に調べてみることにしよう。このことについて、1987年と1988年に行なわれた調査のデータを利用して、それぞれ、
Q6.1 あなたは、あなたの会社は活性化していると考えますか?
1. 活性化していると思う。
2. 活性化していないと思う。
Q6.2 自分の会社は活性化していると思う。
1. Yes
2. No
という質問と他の質問項目との相関関係を調べてみることにする。これらの調査は、いずれも日本生産性本部の経営アカデミー『人間能力と組織開発』コースを舞台として8月末から9月初めにかけて行なわれた質問票調査である。このうち1987年の調査では、日本企業11社のホワイトカラー部門の正社員690人に対して質問票調査が行われ、580人から質問調査票が回収できた。回収率は84.1%であった。1988年の調査では日本企業8社のホワイトカラー部門の中間管理者770人に対して質問票調査が行われ、626人から質問調査票が回収できた。回収率は81.3%であった。
質問Q6.1、Q6.2の2問を除く1987年の調査での50問、1988年の調査での89問の計139問のYes-No形式の質問との間で2×2クロス表を作り、それらのうち相関の高い質問項目として、便宜的に相関係数である V 係数(Cramer's V)の絶対値が0.3より大きなものを拾いあげてみると、1987年の調査では0問、1988年の調査では5問になった。それを、組織の活性化された状態の定義である「組織のメンバーが、(1)相互に意思を伝達し合いながら、(2)組織と共有している目的・価値を、(3)能動的に実現していこうとする状態」に対応させると、
といったように対応が付けられる。( )内は有効オブザーべーション数を示している。
以上のことから、「活性化」のイメージは組織の活性化された状態の定義とほぼ重なっていることがわかる。この調査データだけから、組織の活性化に多様なイメージが重なって存在していることを否定するつもりはない。しかし、組織活性化を組織論的に研究する出発点として、そのイメージの重なった部分の最大公約数的なものとして、Barnard (1938)の組織成立の必要十分条件を定義として採用すること、そして、その上で議論を始めることを本書では提案したい。
組織の特性は大きく二つの種類に分けて考えることができる。一つは長期的な特性で、組織設計の場合には所与と考えられている人的特性およびそれが作り出す組織風土のような固定的なものである。これはトップが変えようと思っても、なかなか変えられない。もう一つは短期的な特性であり、組織形態のように、トップが変えようと思えば変えることができる、いわば可変的な特性である。人的特性のような固定的で長い時間をかけないと変えられない特性は、組織形態のような可変的な組織特性を変える場合には、主に制約条件として作用することになる。そして、この組織形態と環境との間に適合性の問題が生じるのである。つまり、図6.6の図式で示すような関係が成り立っていることが分かる。
図6.6 組織形態と人的特性
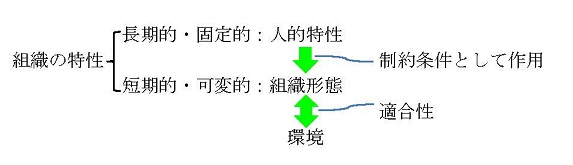
コンティンジェンシー理論では、通常、組織形態と環境(特にその不確実性)との間の適合性が論じられるが、Morse & Lorsch (1970)のように、人間の問題の重要性を主張したごく一部の例外を除くと、組織メンバーの人的特性にはほとんど注意が払われてこなかった(岸田, 1985, p.105)。しかし、組織形態と環境との間の適合性のみを見るのではなく、どの組織形態をとりうるのかについては人的な制約条件を考慮すべきである、というのがまさに数理的組織設計論の示唆する重要な観点である。つまり、単なる環境適応ではなく、人的制約条件のもとでの環境適応の組織設計を考えるということが、組織設計論のより正確な姿なのである。そして、コンティンジェンシー組織とは少なくても前章で考えられた組織形態に関しては、人的制約条件をすべてクリアーした組織なのである。
いままでは、組織の人的特性としてのタイプ1・2・3と可能な組織形態の関係と、組織形態の環境の不確実性への適合性を別々に論じてきた。しかし、この二つの関係が成立するならば、組織特性としてのタイプ1・2・3についても、環境の不確実性への適合性が考えられるはずである。
数理的組織設計論によると、第5章の命題5.3に示されるように、「確実性、リスク、厳密な不確実性のどのケースでも、システム1が効率的であるならば、ピラミッド組織が効率的である。」という関係が成り立っているので、環境の不確実性に適合している組織を考えるのであれば、四つの組織形態のうち、システム1とマトリックス組織の組み合せは考えなくてもかまわない。そこで、残りの三つの組織形態と、タイプ1・2・3の組織の人的特性との関係を、制約条件を考えた選択可能性という形で示し、それにさらに、数理的組織設計論によって明らかにされた組織形態が適合している環境の不確実性の程度を高・中・低と単純化して示してみると、表6.4のようになる。
表6.4 組織特性、組織形態と環境の不確実性
| 組織の人的特性 | 組織形態 | ||
|---|---|---|---|
| P1 ピラミッド組織 システム1 | P2 ピラミッド組織 システム2 | M2 マトリックス組織 システム2 | |
| タイプ1 (受動的器械型) | ○ | × | × |
| タイプ2 (疎外労働者型) | ○ | ○ | × |
| タイプ3 (問題解決者型) | ○ | ○ | ○ |
| 適合している環境の不確実性 | 低 | 中 | 高 |
表6.4のようにすると、組織形態を媒介にして、組織特性と環境の不確実性との間にも、適応性を考えることができる。この表から、タイプ1・2・3の順に、より高い不確実性に対しても、適応的になってくることが分かる。言い換えれば、この表6.4は、環境の不確実性が高まるにつれて、組織は活性化していく必要があるという重要な示唆を与えてくれる。低不確実性下ではタイプ1の組織であっても、唯一とり得る組織形態であるP1、すなわちピラミッド組織でシステム1の「官僚制組織」で適応的になっているのであるが、不確実性が高まってくると、そのうちに、少なくてもタイプ2の組織になっている必要が出てくる。さらに高不確実性下ではタイプ3の活性化組織にならないと、効率的な組織形態をとることができなくなってしまう。ここに、今のような不確実性の高まりつつある時代において、組織の活性化の必要性が叫ばれている一つの背景があるように思われる。
またこうして考えることで、業績と活性化とが必ずしも結び付いたものではないということも明らかになる。つまり、もし環境の不確実性が十分に低くて、組織設計問題の解として、P1つまりピラミッド組織とシステム1の組が効率的であるならば、基本的仮定6.1、6.2を満たしていないような組織であっても、効率的な組織形態をとることができる。したがって、高業績をあげているからといって、活性化された状態であり、コンティンジェンシー組織となっているとはいえないのである。
今回調査対象となった7社のうち、タイプ1に分類された2社がともに子会社であったという事実も、単なる偶然ではないと思われる。一般的に、親会社の段階で、環境の不確実性、不安定性はかなりの程度まで吸収されてしまうので、子会社は低不確実性で安定的な環境にあるといっていい。実際、この2社はどちらも営業・販売部門が弱体であり、そのことは環境の不確実性に対処する必要性があまりないことを示していると思われる。こうした環境にあるからこそ、タイプ1の組織でも十分に高業績をあげることができたのであろう。
数理的組織設計論によって示唆されるような「人的制約条件のもとでの環境適応の組織設計」を考えるとき、I I図は人的制約条件の満足状態を測定し、図示するための手法という位置づけができる。しかし、そうした数理的組織設計論の延長線上での位置づけだけではなく、I I図はそれ自体単独でも別の興味深い経営学的な示唆を与えてくれる。それはI I図のもっている非対称性とでもいうべき特徴である。
一体化度指数が高く、無関心度指数が低いタイプ3が活性化された状態の組織であると既に述べたが、一体化度指数は高いほど良く、無関心度指数は低いほど良いというわけではない。実はタイプ3の隣に崩壊した組織とでもいうべきタイプ4が位置しているのである。日常的によくみかけるこの類の図では、一番「良い」状態の対極(I I図でいえばタイプ2の場所)に一番「悪い」状態があることが多いが、I I図では一番「良い」状態の隣に一番「悪い」状態が位置している。これはタイプ1・タイプ2の組織、特にタイプ2の組織の活性化への道は危険をはらんでいるということを意味している。例えば、組織がどんどん活性化していく中で、個々のメンバーがバランスを失って組織を飛び出していってしまい、離職率が高くなるようなケースを現実の企業でも見ることができる。それは、組織がタイプ3への軌道をはずれて、タイプ4の状態に陥ってしまったことを示している。その意味で活性化は両刃の剣とでもいえるような危険性をもっているわけであり、そうした観点からI I図を眺めることは、活性化について考察する際の助けとなるであろう。
組織メンバーの課業・処遇等に本質的に重大な影響を及ぼすはずの五つの経営施策等の採用・実施状況について、次のような文章を完成させながら答えてもらった: 「経営施策名 は (1. 行われている 2. 行われていない) が、そのことによって、私は (3. 働きがいを感じている 4. 働きがいとは関係ない 5. 働きがいを感じなくなった)。また、会社の活性化には (6. 寄与している 7. 関係がない 8. 悪影響を及ぼしている)。」
無関心度指数は、五つの質問のうち「4. 働きがいとは関係ない」と答えた回答の数である。一体化度指数は、五つの質問のうち、次のどれかのケースに該当する回答の数である。 (a)「3. 働きがいを感じている」と答え、かつ「6. 寄与している」と答えた場合。 (b)「4. 働きがいとは関係ない」と答え、かつ「7. 関係がない」と答えた場合。 (c)「5. 働きがいを感じなくなった」と答え、かつ「8. 悪影響を及ぼしている」と答えた場合。したがって、両指数は0から5までの整数値をとる。
両指数の算出に使われた実際の質問は次の通り。
問 あなたの会社での諸制度の実情について現在あなたが感じていることを、以下の各項目について、文章を完成させながらお答えください。それぞれの( )内で、該当するものを一つ選んで下さい。
以前、企業人を相手にしたセミナーの後で組織の中での意思決定について雑談をしていて、話題が命令、指示の「やり過ごし」の方に向いたとたん「組織の中にあって、上司から出された命令や指示をやり過ごしてしまうなどということはあってはならないことである。」と大きな声である大企業の部長から言われ、話題を変えたことがある。しかし、後になってから、個人的にもっと「やり過ごし」の話を聞きたいという人がやってきた。あってはならないことだとその存在すら一刀両断で切り捨ててしまう人もいれば、それでもあるのだという人もいる。そして驚いたことに、この章で扱っている調査では、やり過ごしのできない部下は無能であるとまで言い切る人さえ現れてきたのである。
従来「やり過ごし」は、やり過ごしをしてしまう人、やり過ごしをさせてしまう人といった個人のキャラクターやパーソナリティーの問題であると片付けられがちであった。確かにそういった側面は否定しきれないし、そこから「やり過ごし」に対する悪い印象も生まれてくると考えられる。しかし「やり過ごし」という組織現象の発生には、こうした個人の側だけではなく、どうやらシステムの側でも何らかの条件が関係しているらしい。研究者にとっても企業人にとっても、何かまだよくわかっていない発生メカニズムや評価すべき機能が隠されているようである。
実は「やり過ごし」のような現象は、直面している問題の大きさが人間の合理性の限界を超えたときに発生することが理論的にわかってきている。そのことを解明してくれるのが、ゴミ箱モデルと呼ばれる意思決定過程モデルとそれに基づくコンピュータ・シミュレーションである。私が冒頭の雑談の際に「やり過ごし」を口にしたのは、ゴミ箱モデルの話が頭の片隅にあったからである。そこでここでは、このゴミ箱モデルについて簡単にその概要を説明した後、命令、指示の「やり過ごし」の現象がどういった意味をもち、どういった条件、要因のもとで発生するものなのかをゴミ箱モデルを使って理論的に考察してみる。そして、より簡単にゴミ箱モデルのシミュレーションを行なうために新たに作成されたSingle Garbage Can Program (SGCP)を使って、条件や要因の影響を吟味し直した上で、さらに高橋(1992c)に基づいて、実際に1991年に行なわれた6社、907人分の質問票調査のデータを用いて、こうした理論的予想が正しいものかどうかを検討した上で、この調査から明らかになった日本企業におけるやり過ごしの実態と果たしている機能についても考察してみたい。
ゴミ箱モデル(garbage can model)は、Cohen, March & Olsen (1972)が端緒となって展開されたモデルである。ここでは原典ともいえるこの論文を中心にして、簡単にその概要を説明しておこう。
ゴミ箱モデルは、組織の意思決定論の学説史上では、決定理論の影響を強く受けている初期の理論の延長線上にあるものとして位置づけられる(March & Olsen, 1976, pp.14-17邦訳pp.18-21)。本書の第Ⅰ部からもわかるように、通常の決定理論では、まずいくつかの選択肢を見いだし、各選択肢のもたらす結果について調べ、それらの結果を目的ないしは選好順序に照らして、最終的に特定の選択肢を決定するという一連の過程を導くものとして選択機会が想定されている。しかし、第4章でも明らかにされたように、決定理論に従えば、意思決定はあまりにも時間とエネルギーを必要とする。それは、合理性に限界のある人間には、到底処理できないほどの過大な要求となっている。近代組織論はこうした組織研究者の決定理論批判をもとに展開されていると言っていいだろう。
ところが、近代組織論によっても、まだ理論と現実との乖離が埋められたわけではない。Cohen, March & Olsen (1972)によれば、例えば組織化された無政府状態を記述するには説明力が貧弱である。ここでいう組織化された無政府状態(organized anarchies)とは、問題のある選好、不明確な技術、そして流動的参加によって特徴づけられた組織のことである。実際、人間の選好が決定理論で言うほどにはすっきりせず、問題のあることが既に第4章で指摘してきた。また、ある選択肢が、ある特定の結果をもたらすという比較的もっともらしい前提も、技術が不確実であいまいなままの状況下では非常に疑わしい。特に技術革新著しい現代においては、むしろ選択肢がどのような結果をもたらすか、やってみるまで、あるいは、やってみて改良、改善努力を行うまでわからないという状況の方が常態なのかもしれない。そして、たとえ組織のメンバーが確定していても、ある種の意思決定、例えばルーチンではない非定型の意思決定に誰が参加するのか、あるいは結果として誰の意見が入ってくるのかは、かなり流動的な側面が強いのも事実である。
このような組織化された無政府状態は、大学の経営・行政において特に顕著であると言われるが、大学についての経験的観察研究によれば、そうした組織では、参加者によって、様々な種類の問題と解が勝手に作り出されては、「選択機会」に投げ入れられている。自らが示されるべき選択機会を捜し求めている「問題」、自らがその答えになるかも知れない問題を捜し求めている「解」、そして、仕事を捜し求めている意思決定者たるべき「参加者」、こういった決定理論や近代組織論の中からはみ出した意思決定過程が繰り広げられるのである。
こうした経験的観察事実に基づいてゴミ箱モデルが考え出された。このモデルで「ゴミ箱」(garbage can)にたとえられているのは選択機会である。組織的意思決定過程においては、あたかもゴミ箱にゴミを投げ入れるように、各参加者が選択機会に対して、問題、解、エネルギーを独立に投げ込み、その選択機会に投げ込まれた問題の解決に必要となる一定量までエネルギーがたまったとき、あたかも満杯になったゴミ箱が片付けられるように、当該選択機会も完結し、「決定」が行われたものとして片付けられるというのである。
より正確には、次のように四つの基本的な概念の再検討を行っている。
これら四つの要素は、互いに比較的独立して、かつ外生的に組織というシステムに対して、流れ込んでいると見ることができる。
Cohen, March & Olsen (1972)は、観察された過程の基本的な特徴を損なわないように、次のような仮定を置き、これらのアイデアをゴミ箱モデルと呼ばれるコンピュータ・シミュレーション・モデルに定式化し、翻訳した。
さらに次のような仮定がおかれる。
エネルギー加法性の仮定: 選択機会が決定に至るためには、各選択機会は、それに投入されている問題のエネルギー必要量の総計と同量の効果的エネルギーを必要とする。つまり、ある時点で、一つの選択機会に属している効果的エネルギーの総量が、エネルギー必要量の総量と等しいかまたはそれを超えると決定がなされる。
このようにゴミ箱モデルは、最も純粋な形では、問題、解、参加者、選択機会の独立で外生的な流れを仮定している(March & Olsen, 1986, pp.17-18 邦訳p.23)。それらは、
によって決まるある方法で結び付けられる。したがって、決定の多くが、選択機会、問題、解、参加者のタイミングの産物である。ゴミ箱モデルでは論理必然的秩序(a consequential order)よりも、むしろ一時的秩序(a temporal order)を仮定していることになる。問題、解、参加者は同時性(simultaneity)によって結び付けられると仮定され(March & Olsen, 1986, p.11 邦訳p.13)、意思決定過程はタイミングに左右されるのである。特に、決定構造、アクセス構造が完全にオープンになっている2がないモデルは未分割版(unsegmented version)と呼ばれ、これまでの文献ではもっとも注意を引いているといわれる(March & Weissinger-Baylon, 1986, p.4 邦訳p.5; p.18 邦訳p.23)。この節でこれから扱うことになるSingle Gabage Can Program (SGCP)もこの未分割版に相当するものである。決定構造、アクセス構造をもった彼らのもともとのシミュレーション・モデルでは次の二つの仮定もおいている。
エネルギー配分の仮定: 各参加者のエネルギーは、各期ではただ一つの選択に投入されているが、各参加者は自分がアクセス可能な選択機会の中でも、決定に一番近い選択機会、つまり他の参加者の投入エネルギーにより前期末のエネルギー不足分が最も小さくなっている選択機会に自分のエネルギーを投入する。
問題配分の仮定: 各問題は各期においてただ一つの選択機会に投入されており、その選択機会は、アクセス可能な選択機会の中から決定に一番近いものが選ばれる。問題間には優先順位は存在しない。
SGCPは未分割版なので、とりあえずこれらの仮定については必要がない。
選択機会と問題、解の関係をもう少し具体的に考えてみよう。まず選択機会の存在は問題の存在を必ずしも意味しない。それは単なる選択機会である。例えば、従業員の採用時期というのは、毎年ほぼ同時期に規則的に訪れる。これは特に何か明示的な問題を伴うものではなく、たまたまそのとき手元にあった採用内定者リストが満足解として、すんなりと決定されることも多い(後述する「見過ごしによる決定」に相当する)。
ところが、多くの場合、本当の意味で問題が存在しなかったわけではない。ただその選択機会では問題が顕在化しなかっただけのことである。例えば、景気が良かったりすると売り手市場となって、時期が来たときに用意できたリストでは、採用内定者の数・質を確保できていなかったり、あるいは結果的に内定者の出身校や出身地が極端に偏っていたりする事態も起こってくる。こうして潜在的に抱えていた問題が姿を現すことになる。採用活動の態勢の問題点、当該企業の知名度の地域的アンバランス、さらには、将来の人員構成はどうあるべきなのかといった将来のビジョンの問題等、様々な問題が次々に提起されることになる。そして、それらの問題に対する善後策が、新たな採用内定者リストとともに解として提示されるということを何度か繰り返しながら、徐々に解決へと向かうことになるのかもしれない(後述する「問題解決による決定」に相当する)。
しかし、採用活動はもともと期限のかなりきつい活動であるから、これだけ多くの問題が噴出してくると、通常はいちいちまともにとりあっていては採用担当者はお手上げの状態となる。そこで、期限内に諸問題を解決することはもともと無理な話と、結局、問題を棚上げにしたまま、ほとぼりがさめるのを待って、あるいは社内のどこかのプロジェクト・チームに先送りされるのを待って、とりあえず今年は、手元の採用内定者リストで行こうという結論になるかもしれない(後述する「やり過ごしによる決定」に相当する)。
実は、先ほどのシミュレーションの仮定からも、全く同様に、次の3タイプの決定が起こると考えられている。
この最後の3のタイプの決定が、この章のテーマである、やり過ごしに該当している。もっとも、「やり過ごしによる決定」というのは意訳である。これまでは、decision making by flightは「飛ばしによる決定」と直訳されることが多かった。しかし、これでは日本の企業では通じないし、実際には人間が問題を飛ばしているのではなく、問題の方が飛んで行ってしまうまで、人間の方はじっとやり過ごして待っているわけなので、本書では「やり過ごしによる決定」という訳語を提案したい。
Cohen, March & Olsen (1972)は、このモデルにしたがい、コンピュータ・シミュレーションを行い、通常いわれる「問題解決による決定」は一般的ではなく、特に問題の負担が大きいときには、問題の見過ごし、やり過ごしによる決定の方が、実は通常の決定スタイルとなることなどの知見を得ている。
ところで、Cohen, March & Olsen (1972)の作ったシミュレーション用のプログラムはFORTRANで書かれ、同論文の最後に付録として掲載されているが、決定構造やアクセス構造を組み込んでいるために複雑で長いものになっている。そのため、プログラムの内容を理解するのが困難であるし、修正も難しい。また乱数列をデータとして与える形式をとっているために、長い期間のシミュレーションには適さない。ここでこれから実際に行なってみる1,000回の決定を行なうまでの数千期間のシミュレーションでは、BASICのようなコンピュータ言語の乱数発生関数を使うようにしなければ使用に耐えない。乱数発生関数をプログラムに組み込んでおけば、数百万期間のシミュレーションも簡単に行なうことができる。そこでここでは、決定構造、アクセス構造を考えない未分割版を
と定式化することにしよう。このことによって、シミュレーション・プログラムを非常に簡単にすることができる。そこでこうした観点からSingle Garbage Can Program (SGCP)と呼ばれるプログラムを新たに作成した。これはBASICで書かれ、次のようになる。
110 '***************************************************************************SGCPでは、選択機会に参加者からのエネルギー(EP)または問題(エネルギー必要量 ERP)の少なくともどちらかが投げ込まれて、はじめて選択機会が出現したと考え、カウントすることになっている(行番号280)。このモデルで問題の負荷(load)量を決める負荷係数(LC)を色々変えることによって(行番号180)、問題の負荷量の決定スタイルに与える影響について調べてみることにしよう。いま解係数 SC=1、決定回数 K=1,000回 と設定しておいて(行番号170と370)、シミュレーションを行なってみた結果は、表7.1のようにまとめられる。
表7.1 問題の負荷と決定のタイプ
| 負荷 係数 LC | 決定1回 に要した 平均期間 | 決定のタイプ | 最長考決定 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 問題 解決 | 見過 ごし | やり過ごし | 出現 回 | 所要 期間 | 決定タイプ | ||||
| 解決 | 放置 | 計 | |||||||
| 0.1 | 2.034 | 450 | 349 | 150 | 51 | 201 | 71 | 12 | 問題解決 |
| 0.2 | 2.146 | 432 | 336 | 176 | 56 | 232 | 261 | 14 | やり過ごし解決 |
| 0.3 | 2.382 | 419 | 331 | 169 | 81 | 250 | 57 | 143 | 問題解決 |
| 0.4 | 2.575 | 397 | 331 | 172 | 100 | 272 | 50 | 146 | やり過ごし解決 |
| 0.5 | 2.720 | 374 | 330 | 176 | 120 | 296 | 45 | 163 | やり過ごし解決 |
| 0.6 | 3.290 | 352 | 333 | 178 | 137 | 315 | 41 | 400 | やり過ごし放置 |
| 0.7 | 3.847 | 299 | 352 | 179 | 170 | 349 | 36 | 410 | 問題解決 |
| 0.8 | 4.307 | 270 | 351 | 167 | 212 | 379 | 29 | 513 | やり過ごし放置 |
| 0.9 | 4.819 | 234 | 347 | 167 | 252 | 419 | 24 | 514 | 問題解決 |
| 1.0 | 5.549 | 193 | 357 | 164 | 286 | 450 | 22 | 516 | やり過ごし放置 |
まず表7.1から問題の負荷が大きくなると、決定1回当りに要する平均期間がどんどん長くなっていくことがわかる。そして、表7.1から明らかに、負荷係数が大きくなって問題の負荷が大きくなるほど「問題解決」という決定のタイプが減り、それに代わって「やり過ごし」、特に「やり過ごし放置」が増える傾向のあることがわかる。参加者のエネルギーに比べて問題の負荷量が大きくなると、結局、参加者の存在は小さなものとなり、参加者のエネルギー投入の様子にあまり関係なく、問題の去就によって意思決定が左右されるようになる様子が見てとれる。
それらに比べて、「見過ごし」「やり過ごし解決」は負荷係数にあまり関係なく安定している。このうち「見過ごし」はSGCPの場合、理論的には確率1/3で発生するようになっている。なぜなら、「見過ごし」は選択機会の最初に EP>0 かつ ERP≦0 となったときに発生するが、このプログラムでは
Pr{EP>0}=Pr{ERP≦0}=1/2
となるように設定してある。さらに EP≦0、ERP≦0 のときは、選択機会は出現しなかったという扱いになるので、「見過ごし」の発生確率は
Pr{EP>0 かつ ERP≦0 | EP>0 または ERP>0}
=Pr{EP>0 かつ ERP≦0}/Pr{EP>0 または ERP>0}
=(1/4)/(3/4)=1/3
となるからである。実際、表7.1では「見過ごし」の発生は1000回中330~357回程度となっている。
以上のことから、問題の負荷が大きくなると、「問題解決」による決定が減り、その分「やり過ごし」による決定、特に「やり過ごし放置」が増えることが確認できた。
ゴミ箱モデルは、その後、確率過程モデルによる分析なども行われたが(Padgett, 1980a; 1980b)、現在では、そうしたモデル自体の分析よりも、むしろ現実の経営管理過程の分析に、分析枠組みとして用いられるようになっている。March & Weissinger-Baylon (1986, ch.2)にはこうした文献のサーベイがあるので参考になるが、より具体的には、
というような3要件の揃った状況での意思決定を、あいまい性下の意思決定(decision making under ambiguity)と呼び、分析を行なうのである(March & Weissinger-Baylon, 1986, p.1 邦訳p.1)。このうち3は、ゴミ箱モデルの理解を前提にすれば、より正確には、「そのとき同時に複数の問題が存在することで、意思決定者の負担が大きく、各問題に対する注意が薄められる。」というべきであろう。いずれにせよ、この3要件が揃ったときには、意思決定過程は素朴な決定理論の枠組みから外れ、ゴミ箱モデルの様相を呈することになる。
あいまい性下の意思決定といえるような現実の経営管理過程の分析に、ゴミ箱モデルが分析枠組みとして用いられている研究としては、彼ら自身による March & Olsen (1976)が挙げられ、この中には、アメリカ、オランダ、ノルウェーの大学経営についての詳細な事例研究が含まれている。さらに、March & Weissinger-Baylon (1986)によれば、軍事組織の意思決定過程にも、戦時、平時を問わず、ゴミ箱モデルがもつ多くの特徴を見ることができるという。
経営の分野での分析枠組みとしての応用という点で注目されるのは、Lynn (1982)で、新しい製鋼技術が日米両国の鉄鋼産業にいかにして導入されたのか、その経緯をゴミ箱モデルを分析枠組みとして使って描いている。新しい製鋼技術とは、純酸素上吹き転炉(BOF; basic oxygen furnace、LD転炉とも呼ばれる)である。これは、レンガで内張りされた炉で溶融した鉄を精錬する際に純酸素を上から吹き込む方法で、1949年にスイスの小さな製鋼会社の研究チームが実験に成功し、オーストリアのフェースト社とアルピネ社がそれぞれ1952年、1953年に実用BOF工場の稼働を始めたものである。日本では八幡製鉄が1957年、日本鋼管が1958年に導入したのに始まって、このBOFを速やかに導入したことで、1960年代に日本の鉄鋼業の国際競争力が飛躍的に伸びたといわれる。Lynnによれば、標準的な意思決定モデルは、BOFの後発組に見られる決定過程には符合するが、先発組の決定過程には当てはまらず、ゴミ箱モデルが符合していた。例えば、八幡製鉄では、生産能力を拡充しようとの決定が行われる前に、既にBOFを見いだしていたというように、問題がはっきりする以前に解が現れていた。また、日本鋼管では、技師や研究所の研究員、取締役、社長が、助言を求められる形や積極的に旗振りをする形で、さまざまな時、所でかかわっていたというように、決定センターがはっきりしなかった。そして、BOFという代替案、解は、誰かに発見されるのをじっと待っていたのではなく、BOFのプロモーターの積極的な売り込み努力に見られるように、「提案者」を積極的に探していたのである。
そこで、以上のようなゴミ箱モデルから得られた知見をもとに、日本の企業で「やり過ごし」がどれほど一般的なものなのか、そして、あいまい性下の意思決定とやり過ごしとの間にどのような関係があるのかを調べるために、調査が企画実施された。この調査の結果について高橋(1992c)をもとにして簡単にまとめておこう。この調査で調査対象となったのは、日本生産性本部の経営アカデミー『人間能力と組織開発』コースの1991年度の参加者の所属企業6社である。調査は質問調査票の質問を作成する前のヒアリング調査と、質問調査票を使った質問票調査、そしてその調査結果を手にしてから行なったフォローアップのヒアリング調査の3段階に分けて行われた。
第1段階のヒアリング調査では、1991年6月14・15の両日に、合宿形式で集中的に1社平均120分程度をかけて、各社の会社の概要、組織的特徴、問題点、社風などを中心に、報告、質疑応答等が行われた。さらに、そこで出された問題意識を基にして、この各社1人ずつの6人と筆者の計7人からなるグループで、相互に何回かのヒアリングを行い、会社・職場内の現象、個人の仕事に対する意識をできるだけ具体的にリストアップしていく作業を行った。この過程で、様々な質問項目が挙げられたが、最終的には筆者がそれらを整理する形で、あなたの仕事への意欲・やりがいに関する質問(Ⅱ1~15)、あなたの会社・職場の雰囲気に関する質問(Ⅲ1~15)、あなたの会社の意思決定スタイルとコミュニケーションに関する質問(Ⅳ1~15)、あなたと会社との関わりに関する質問(Ⅴ1~15)、あなたの会社・職場に対する評価に関する質問(Ⅵ1~15)の計75項目のリストを作成し、これをYes-No形式の質問にまとめた。
調査の第2段階では、各社で質問票調査を行った。まず、各社のヒアリング対象者の所属する、もしくはそれに比較的近いホワイトカラーの部門を選び、さらにその中において、組織単位を一つまたは複数選び、その組織単位の構成員に対して、原則として、全数調査を行った。各社において選ばれた組織単位数は3から9まで幅があるので、各社の調査対象者数には90人から358人まで開きがあるが、総組織単位数は30ヶ所、総調査対象者数は1,017人、組織単位当りの平均調査対象者数は33.9人となっている。このような方法によって調査対象に選ばれた6社1,017人に対して、1991年8月28日(水曜日)に各社一斉に質問調査票が配布され、記入してもらった上で、9月2日(月曜日)までに回収するという形で、質問票調査が行われた。その結果、907人から質問調査票が回収できた。回収率は89.2%であった。回収された質問調査票は、あらかじめ決められた指示に従って、各社の担当者によって点検された上で、筆者がクリーニングを行った。
調査の第3段階については、後の§7.2.cで述べることにして、まずは質問票調査の結果について述べることにしよう。
調査データの分析は鍵となる次のYes-No形式の質問を中心に行なわれた。
Ⅳ7. 指示が出されても、やり過ごしているうちに、立ち消えになることがある。
1. Yes 2. No
この質問に対しては、597人(66.3%)がYes、303人(33.7%)がNoと答えた。つまり、3分の2人がやり過ごしを経験していることになる。このうち、Yesと答えた人の比率をやり過ごし比率と定義すると、年齢・職位階層別のやり過ごし比率は表7.2のようになる。この表7.2によると、年齢でいうと「30代」、職位でいうと「課長」のやり過ごし比率が高くなっていることがわかる。「30代の課長」ともなると、80%以上の人が指示をやり過ごしているうちに、その指示が立ち消えになることを経験している。第1段階のヒアリング調査の結果から、今回の調査対象企業に関していえば、組織の中で、実は一番忙しいのが、この「30代」「課長」という階層の人たちであるということがわかっていたので、これはゴミ箱モデルのシミュレーションによる知見、すなわち、問題の負担の大きいときには、問題の見過ごし、やり過ごしによる決定が多くなるという結論と合致しているといえる。
表7.2 年齢・職位階層別のやり過ごし比率
| 年齢 | 職位 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1. 部長 | 2. 課長 | 3. 係長・主任 | 4. 一般 | 全体 | ||||||
| 1. 20-24 | 100.0 | (3) | 47.3 | (55) | 50.0 | (58) | ||||
| 2. 25-29 | 100.0 | (4) | 73.7 | (19) | 65.5 | (142) | 67.3 | (165) | ||
| 3. 30-34 | 87.0 | (23) | 75.8 | (66) | 65.3 | (75) | 72.6 | (164) | ||
| 4. 35-39 | 75.0 | (4) | 82.5 | (57) | 60.7 | (61) | 69.6 | (23) | 71.0 | (145) |
| 5. 40-44 | 72.4 | (29) | 68.6 | (51) | 58.8 | (51) | 73.9 | (23) | 66.9 | (154) |
| 6. 45-49 | 81.8 | (22) | 50.0 | (26) | 50.0 | (42) | 66.7 | (6) | 58.3 | (96) |
| 7. 50-54 | 64.3 | (14) | 75.0 | (16) | 37.0 | (27) | 50.0 | (4) | 54.1 | (61) |
| 8. 55- | 33.3 | ( 3) | 50.0 | (2) | 50.0 | (10) | 100.0 | (5) | 60.0 | (20) |
| 全体 | 72.2 | (72) | 73.7 | (179) | 60.9 | (279) | 63.7 | (333) | 65.6 | (863) |
次に、この質問Ⅳ7とそれ以外の74の質問項目との間の相関をとり、その相関の高かった質問項目の上位10項目の質問文を相関係数の絶対値順に並べると、次のようになる。(2×2クロス表なので、クラマーのV係数とピアソンの積率相関係数rとは一致する。詳しくは高橋(1992b)を参照のこと。)
| VI11. | 基準・規程・マニュアルがあるにもかかわらず、有効には利用されていない。 |
| V3. | チャンスがあれば転職したいと思う。 |
| IV15. | 複数の系統から指示を受けることがある。 |
| VI13. | 長期的展望に立った仕事というより、短期的な数字合わせになりがちである。 |
| V15. | 自分の仕事上の成果に対する上司の評価は、適切で公平だと思う。 |
| IV4. | 互いに納得のいくまで議論ができる雰囲気がある。 |
| IV2. | 本音の議論は、就業時間中というより、社外で行うことが多い。 |
| III13. | 評価は、業績、貢献度でというより、上司の好き嫌いで判断される傾向がある。 |
| IV5. | 議論を議論のままで終らせずに、委員会の組織化や根回し等、実行に向け乗り出すことが多い。 |
| VI10. | 上司から仕事上の目標をはっきり示されている。 |
この他にも、福利厚生面の充実との間にも相関が見られたが、これについては3重クロス表を作ってみると、疑似相関であるらしいことがわかったので、このリストからは除いてある。(より具体的には、調査対象企業を公益事業とそれ以外の非公益事業とに分けた上で、それぞれクロス表を作って調べてみると、相関係数はそれぞれかなり小さくなり、しかも、非公益事業では指示のやり過ごしが多く、福利厚生面での充実が立ち後れているのに対して、公益事業では、福利厚生面でも充実しているし、指示のやり過ごしも比較的少ないということがわかった。したがって、指示のやり過ごしと福利厚生という直接的には本来無関係なはずの変数が、実はともに企業の業種、業態、市場環境と密接に結び付き、これらが先行変数となっているために、疑似相関が見られると考えられる。高橋(1992b)も参照のこと。) これら10の質問項目と質問Ⅳ7との相関係数及び会社別に見た各質問に対するYes比率は表7.3によって示されている。
表7.3 やり過ごし(質問IV7)と相関の高かった上位10項目(相関係数(V係数)の絶対値順)
| やり過ごし(質問IV7)との相関 | 会社別に見た各質問に対するYes比率 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 相関の高かった上位10項目 | 相関係数 | A社 | B社 | C社 | D社 | E社 | F社 | 全体 | χ2 |
| IV7. 指示やり過ごし可 | 1.000 *** | 62.3 | 81.1 | 53.2 | 54.5 | 60.6 | 60.0 | 66.3 | 51.721 *** |
| VI11. 基準有効利用まだ | 0.234 *** | 64.7 | 79.6 | 52.2 | 51.2 | 68.5 | 36.9 | 64.4 | 76.260 *** |
| V3. 機会があれば転職 | 0.202 *** | 28.1 | 52.2 | 31.3 | 19.2 | 46.5 | 46.4 | 40.1 | 56.788 *** |
| IV15. 複数系統から指示 | 0.198 *** | 67.6 | 75.5 | 65.2 | 53.3 | 63.0 | 52.4 | 66.1 | 29.247 *** |
| VI13. 短期的数字合わせ | 0.197 *** | 85.9 | 88.0 | 81.3 | 67.8 | 81.9 | 78.6 | 82.3 | 26.498 *** |
| V15. 上司の評価は適切 | -0.195 *** | 65.9 | 74.3 | 72.1 | 79.3 | 72.0 | 63.4 | 72.1 | 9.593 + |
| IV4. 納得いくまで議論 | -0.188 *** | 31.2 | 46.7 | 36.0 | 53.7 | 46.5 | 57.6 | 45.0 | 23.984 *** |
| IV2. 本音の議論は社外 | 0.186 *** | 63.2 | 49.2 | 53.6 | 38.8 | 32.3 | 57.6 | 48.9 | 33.709 *** |
| III13. 上司の好嫌で評価 | 0.173 *** | 54.0 | 32.1 | 44.5 | 29.8 | 40.9 | 58.3 | 40.4 | 37.428 *** |
| IV5. 議論は実行に直結 | -0.170 *** | 30.8 | 37.1 | 44.1 | 55.0 | 57.5 | 38.8 | 42.5 | 31.127 *** |
| VI10. 上司から目標明示 | -0.169 *** | 65.4 | 66.0 | 57.7 | 65.3 | 68.5 | 50.6 | 63.7 | 10.207 + |
さらに各変数を標準化した上で主成分分析を行なうと、各主成分に対する固有値は 2.568, 1.257, 0.961, 0.951, 0.902, 0.765, 0.728, 0.647, 0.634, 0.587 となり、第三主成分以下は1に満たないので、第一主成分、第二主成分だけを考えることにする。対応する固有ベクトルによって求めた重み係数は表7.4に示されているが、これによると、第一主成分は、上司の好き嫌いで評価され、上司の評価は適切さに欠けており、納得のいくまで議論が行なわれず、あいまいなままで、上司からの目標明示がないというように、「上司のあいまい性」を表している。それに対して、第二主成分は、基準・規程・マニュアルがあるにもかかわらず、有効に利用されておらず、複数系統からの指示があり、しかも長期的展望に立った仕事というよりも短期的数字合わせに終ることも多いなど、ゴミ箱モデルが示唆している本来のあいまい性を表している。これを「上司のあいまい性」と区別するために「状況のあいまい性」と呼ぶことにしよう。こうしたことから、今回の調査対象企業にとっては、やり過ごしの要件としては、ゴミ箱モデル本来の「状況のあいまい性」だけではなく、「上司のあいまい性」も重要であったことがわかる。
表7.4 主成分分析
| やり過ごし(質問IV7)と相 関の高かった上位10項目 | 固有ベクトル | |
|---|---|---|
| 第一主成分 | 第二主成分 | |
| VI11. 基準有効利用まだ | 0.283 | 0.480 |
| V3. 機会があれば転職 | 0.215 | 0.325 |
| IV15. 複数系統から指示 | 0.205 | 0.453 |
| VI13. 短期的数字合わせ | 0.316 | 0.351 |
| V15. 上司の評価は適切 | -0.374 | 0.259 |
| IV4. 納得いくまで議論 | -0.369 | 0.279 |
| IV2. 本音の議論は社外 | 0.294 | -0.293 |
| III13. 上司の好嫌で評価 | 0.376 | -0.310 |
| IV5. 議論は実行に直結 | -0.321 | -0.059 |
| VI10. 上司から目標明示 | -0.354 | 0.074 |
| 固有値 | 2.568 | 1.257 |
そこで、各社ごとに第一主成分、第二主成分の平均得点を求めて、それをもとに各社をプロットしてみると、図7.1が得られる。これによると、やり過ごし比率が81.1%と最も高かったB社は、「上司のあいまい性」、「状況のあいまい性」ともに高かったのに対して、やり過ごし比率が60%台の3社については、A社、F社は「上司のあいまい性」が高く、E社は「状況のあいまい性」が高いというように、ややタイプの異なっていることがわかった。
図7.1 主成分得点による6社の位置づけとやり過ごし比率
上司のあいまい性も仕事のあいまい性もともに高く、6社中やり過ごし比率が81.1%と最も高かったB社について、調査の第3段階としてフォローアップのヒアリング調査を行なった。その結果、多くのやり過ごしの発生原因があげられた(狩谷他, 1992)。それらは、企業内におけるやり過ごしの実態を描写していて興味深い。これを「上司のあいまい性」「状況のあいまい性」といった切り口で次のように整理することができる。
さらに、状況のあいまい性の高いE社における第3段階のヒアリング調査から、やり過ごしの発生原因とその機能に関して、特に、その機能面を積極的に評価する興味深い結果が得られた(狩谷他, 1992)。つまり「状況のあいまい性」に対応した「オーバーロード状況におけるスクリーニング機能」である。
E社の調査対象部門は業務量と要員のバランスを欠いていて、慢性的にオーバーロードの状態で仕事をしている。このことが図7.1でのE社の位置を決定づけているといっていい。このような状況で上司の指示命令のすべてに応えることは不可能である。部下は、自ら優先順位をつけ、上司の指示命令を上手にやり過ごすことで、時間と労力を節約し業務をこなしている。それができない部下は「言われたことをやるだけで、自分の仕事を管理する能力がない」「上からの指示のプライオリティづけができない」という評価をされることになる。実際に、次のような評価基準を明かした管理者もいた。
しかし他方で、「上司のあいまい性」に対応した「バカ殿状況におけるフィルター機能」についても指摘があった。実はE社の今回の調査対象は、いわゆる本社の部門であったが、人事異動が頻繁に行なわれるE社では、支社・支店で自分の所掌業務に関しての専門知識を十分持ち合わせていない管理者も多い。こうした場合、その業務に長年従事し、「職人」としての専門知識をもつ部下にとっては、反論するのもばかばかしい指示が時としてなされる。しかし、面と向かって上司の指示がいかにナンセンスなものであるかを部下が立証しても、それを受け入れる度量の広さを上司が持ち合わせていない場合、職場の人間関係はぎくしゃくするだけなので、的外れな指示は部下のやり過ごしによって濾過され、上司に恥をかかせずに、正当な指示に対する業務だけがラインに流れることになる。管理者の気まぐれ的なわずかな変更も、支社・支店の現場を振り回すことになるので、そうした指示を出したがる上司に仕える部下は、指示をやり過ごすことで、リーダーの異質性の表出を抑え、組織行動の安定化をもたらしているともいえる。
その他、意図したわけではなく、不本意ながらもできなかった指示、あるいは忘れられた指示が時の経過とともに結果的にやり過ごされてしまう場合ももちろんあるとされている。しかし、スクリーニング機能、フィルター機能ともに、やり過ごしが部下の側の能力を発揮する場としての側面をもっていることを示唆している。このことは表7.2にもあったように、30代の課長にやり過ごしの経験が多いこととも符合している。B社でのヒアリング結果からもわかるが、ゴミ箱モデルが想定しているような「状況のあいまい性」がある場合には、やり過ごしは、部下が行使すべき「正当な」意思決定方法なのかもしれない。
またフィルター機能は、「上司のあいまい性」を回避する際に、やり過ごしが生じていることを示している。実際、図7.1でも上司のあいまい性が高いという特徴のあるA社については、第3段階のヒアリング調査の結果、たまたま現在の部長クラスの数人のキャラクター、パーソナリティーが、この調査結果に大きく影響しているらしいということがわかっている。このような場合、B社のヒアリング結果も示すように、組織運営上はやはり問題も多い。上司の人選等で改善、工夫の余地があるように思われる。
以上のことから、日本の企業では、やり過ごしの現象はごく普通に見られるということ、そして、それはゴミ箱モデルが明らかにしたように、あいまい性下の意思決定過程で発生しているということがわかった。さらに、やり過ごしは、中間管理職、特に30代の課長クラスが頻繁に経験しているということにも象徴されるように、問題の負担が大きすぎて、オーバーロード状況に陥っている組織を、ゴミ箱モデルが想定しているような「状況のあいまい性」の下で、できるだけ有効に機能させるという側面だけでなく、上司の不安定さや頼りなさに起因する「上司のあいまい性」を上手に回避することで組織行動を安定化させる側面ももっていることが明らかになった。シミュレーションでも明らかなように、やり過ごしは、人的条件を一定にしておいても、高い「あいまい性」下では論理的に自然に発生する現象なのであるが、実際には「上司のあいまい性」が深く関与していることも明らかになったのである。これを是とするか非とするかで、本章の冒頭にもあるように、やり過ごしが良い現象か悪い現象か、評価が分かれることになる。
ゴミ箱モデルは「あいまい性」で呼ばれるような状況、すなわち問題の大きさが人間の問題解決能力、合理性を超えてしまったような状況に発生するであろう組織的現象や事態を予想し、その発生メカニズムを説明するためのモデルである。その意味では、本章で特に重点的に取り上げた「やり過ごし」の現象は、組織という装置をもってしても、人間が対処しきれないような状況に直面したときに、人間がいかにしてその事態を乗り切るのか、そして人間はいかにして合理的な意思決定を行いうるのかを端的に表しているといえる。
これまで決定理論と組織論について考えてきたが、本書の最後に、組織の理論の中でも、決定理論のモデルが明示的かつ直接的に取り入れられている分野である動機づけのモデルについて考えてみよう。ここでは、代表的な2モデル
VroomやAtkinsonのモデルは認知的モデル(cognitive model)とも呼ばれ、人間が複数の代替的行為コースの中から行う選択が、行動と同時に生起する心理学的事象と法則的に関連していると仮定している。選択はそうした諸力の相対的強度に依存するものと考えるのである。この考え方は、基本的に決定理論の考え方と類似したものである。ここでは、両者を比較検討することで、実際に組織の中で行なわれる意思決定が決定理論やゲーム理論で考えられているように、本質的に期待効用原理によるものと考えてしまってよいのかどうかを考察してみることにしよう。
そこでまず、Vroom (1964, pp.14-18 邦訳pp.15-20)も参考にしながら、ここで扱う二つのモデルを構成する共通で主要な3概念を決定理論と関係づけて、まとめておこう。
以上のような3概念の共通性を念頭に置いた上で、まずは期待効用原理そのものともいえるVroomのモデルから見てみることにしよう。
Vroom (1964)のモデルは期待理論(expectancy theory)とも呼ばれ、ある特定の行為を行わせようとする動機づけに関心を向けた。いま結果 j の誘意性すなわち効用を Vj とし、pi( j) を行為 i が結果 j をもたらす主観確率とする。このとき、ある人に行為 i (i=1, ..., l) を遂行するように作用する力(force) Fi は、
Fi=fi (Σj=1m pi( j) Vj), i=1, ..., l (8.1)
となるとされる(Vroom, 1964, Proposition 2)。ただし、fi'>0 で fi は単調増加関数である。
後述するAtkinson型のモデルとの決定的な違いは、結果の誘意性 Vj, j=1, ..., m の値の決まり方である。Vroomは、結果の誘意性はそれと結び付いた他の結果の誘意性から導き出されると考えていた(Vroom, 1964, Proposition 1)。例えば図8.1のように、(8.1)式の中にある誘意性を第1次の結果 j の誘意性 V1j とすると、これは第2次の結果kの誘意性 V2k とその結果 k の獲得に対する第1次の結果 j の手段性(instrumentality) Ijk から、次の(8.2)式のように求められると考えた。
V1j=gj (Σk=1nIjkV2k), j=1, ..., m (8.2)
ただし、-1≦Ijk≦1。また gj'>0 で gj は単調増加関数である。
図8.1 Vroom型の動機づけモデル
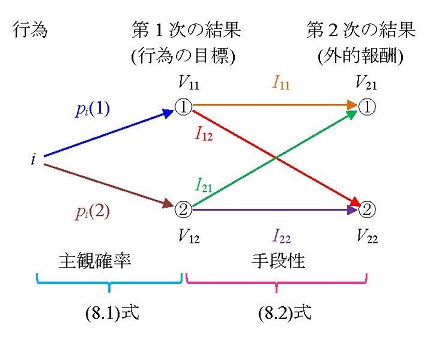
実は、Vroom (1964)自身は第1次の結果と第2次の結果という区別をしていないが、両者を区別しておかないと、誘意性の間にはこの(8.2)式が与えられているために、誘意性はその連立方程式を代数的に解くことによって求められるべきものであるということになりかねない。そこで、一般には第1次の結果と第2次の結果とを区別しておく。第1次の結果の複合体がいわゆる行為の目標に相当しており、第2次の結果は外的報酬に相当したものであると考えられている(Deci, 1975, p.119 邦訳p.134)。Vroom理論の解説や解釈も実質的におおむねこの区別を行っている。いずれにせよ、図8.1にも示されるように、 (8.1)式の中の結果の誘意性は、その結果と結び付いた他の外的報酬のようなものの誘意性から、主観確率 pi( j) とは独立に導き出されると考えられているのである。
それでは、Atkinson (1957)の動機づけモデルはどうであろうか。実は、Vroomのいうところの誘意性つまり効用がどのように決められるかという点で、Atkinsonは別の考え方をしていた。Vroomのモデルでは、期待効用原理と同様に、外的報酬の効用のように、効用はそれをもたらす確率とは独立に決められていたのに対して、Atkinsonのモデルでは、効用はそれをもたらす確率と連動して決まると考えたのである。Vroomの考えた効用は、期待効用原理で考えられていたくじの賞金の効用のようなものであるが、Atkinsonはそうは考えなかった。
まず、Isj を目標 j の成功の誘因価(incentive value of success)とし、Ifj を目標 j の失敗の誘因価(incentive value of failure)とする。ここで、成功の誘因価とは人が目標jを達成した際に感じるプライドで、その目標が達成困難なほど高い誘因価をもつ。他方、失敗の誘因価とは失敗に伴う恥や困惑といった不快の情緒であり、負の値をとるが、その目標の達成が容易なものであったほど、失敗したときのダメージはひどく、失敗の誘因価の絶対値は大きくなる。
また、Ms を成功への動機(motive to approach success)とし、Mf を失敗回避動機(motive to avoid failure)とする。両方とも比較的安定したパーソナリティー的特性で、その値は各個人については状況にかかわらず定数であると考えられる。そして、成功の効用、失敗の効用は対応する誘因価 Isj、Ifj とパーソナリティー的特性である動機 Ms、Mf のそれぞれの積で決まると考えたのである。
以上のことから、あとは成功の確率と失敗の確率がわかれば、期待効用が求められるわけで、目標 j の達成状況に接近したり回避したりする合成的モティベーション(resultant motivation) Rj は
Rj=p( j)Ms Isj+(1-p( j))Mf Ifj (8.3)
と表される。ここで、p( j) は目標 j の成功の主観確率である。
ここまではVroom型のモデルつまり期待効用原理とほぼ同じである。ここから先の誘因価の定義つまり効用の定義が、Vroom型のモデルとは本質的に異なる。これまでの話からもわかるように、成功の確率 p( j) は目標 j の成功の容易性を表していることになるし、他方、1-p( j) は目標 j の成功の困難性と考えられる。Atkinsonは、成功の誘因価は達成が困難であった方が高く、失敗の誘因価は達成が容易だったはずのものほど負の低い値をとるという誘因価のもっている意味から、誘因価 Isj、Ifj がそれぞれこの目標 j の成功の困難性、容易性の線型関数になると仮定した。そして、その線型関数という関係をさらに単純化して、誘因価と目標 j の成功の確率 p( j) との間に次のような関係を仮定するのである。
Isj=1-p( j), Ifj=-p( j)
この関係を用いれば、合成的モティベーションを表す(8.3)式は
Rj=(Ms-Mf) p( j)(1-p( j)) (8.4)
となり、成功への動機 Ms と失敗回避動機 Mf という二つのパーソナリティー的特性を表す定数と目標 j の成功の確率 p( j) によって、合成的モティベーション Rj が決まることになる。この (8.4)式の中の個人ごとに定まる定数である Ms-Mf は、チャレンジの際の成功への動機から失敗回避動機を引いたものであり、この変化を求める傾向を個人の変化性向(propensity to change)とよぶこともある(高橋, 1993a)。
このモデルでは、誘因価が成功の確率によって決まるということを仮定したことで、「目標達成」ということのもたらす満足は、目標達成それ自体にのみ関係し、目標達成以外には明白な報酬がまったくないことになる。このことは、Vroom型のモデルと比べて際だった特徴になっている。当該活動の他には明白な報酬がまったくないのに活動に従事するわけであり、期待効用原理で考えたように賞金目当てにくじを引くわけではない。あえて言えば、くじを引くこと自体が目的となっている。このように、Atkinson型のモデルでは後述する内発的動機づけだけが問題になっていることになる。
外的報酬による動機づけを考えたVroom型のモデルでは、もし同じ外的報酬 k をもたらすパスに、容易なパスと困難なパスの二つのパスがあるときには、人は容易なパス、すなわち、確率 pi( j) と手段性 Ijk の大きいパスを選ぶことになるだろう。なぜなら、外的報酬の期待値が高くなるからである。しかし、内発的な動機づけを考えたAtkinson型のモデルでは、より困難なパスを選ぶかもしれない。なぜなら、合成的モティベーションを表す(8.4)式の Rj の式からも明らかなように、個人の変化性向が正、つまり、Ms-Mf>0 ならば、p( j)=1/2 のときに最大の内的報酬が得られるからである。したがって、外的報酬による動機づけは、目標成功の困難性が低いほど大きくなるが、他方、内発的動機づけは、目標の困難性が一定の最適水準に高まるまで増大するのである(Deci, 1975, p.117 邦訳p.132)。つまり、Vroom型のモデルではできるだけ容易な道へと向かってしまうのに対して、Atkinson型のモデルでは、個人がある程度は困難なことにチャレンジするように動機づけられることになると結論するのである。
このように、この2タイプの動機づけモデルによって導かれる結論は異なる。それでは、実際には、仕事をする際の満足感である職務満足は、一体どこから来ているのだろうか。Vroomの考えたように、くじの期待効用のごときものなのだろうか。それともAtkinsonの考えたように、くじの期待効用とは異なる内発的なものなのだろうか。
Herzbergの動機づけ衛生理論(motivation-hygiene theory)はヒントを与えてくれる。Herzbergらは、米国ピッツバーグ(Pittsburgh)市の企業9社の技術者と会計担当者、約200人を対象にした横断的な面接調査を行なった。この面接調査では、彼らの職務について例外的に良い感じをもった時、あるいは例外的に悪い感じをもった時を思い出してもらい、その時にどんな事象が起こったのかを詳細に話してもらうという方法がとられた(Herzberg et al., 1959, ch.3, pp.141-142)。その結果、次のような事実発見が得られたという(Herzberg et al., 1959, p.80)。
Herzberg et al. (1959, pp.113-114)は、これらの2組の要因は二つの分離したテーマを有していると考えた。つまり、職務満足をもたらす1の満足要因(satisfier)は自分の行っている職務そのものと関係していると考えられるが、職務不満足をもたらす2の不満足要因(dissatisfier)は自分の職務ではなく、それを遂行する際の環境、条件と関係しているというのである。そして、1の満足要因は動機づけ要因(motivators)と呼ばれ、2の不満足要因は、もっぱら職務不満足を予防するための環境的要因なので、衛生要因(factors of hygiene)と呼ばれることになる。これが動機づけ衛生理論の概要である。
この動機づけ衛生理論に対して、その後、Herzberg自身のものも含め、多くの追試が行われ、Herzberg (1966, chs.7-8)で多数紹介されている。そのうち、復元調査だけでも9研究が取り上げられており、もともとの調査も入れて、17母集団に対する10研究で、重複しているものも入れて100以上の要因が調べられ、そのうち、動機づけ衛生理論の予想と違う結果になったのはわずか3%にも満たないことが紹介されている(Herzberg, 1966, p.125邦訳p.141)。以上のことから、Herzbergの動機づけ衛生理論はかなり真憑性が高いと考えるべきであろう。
動機づけ衛生理論の真憑性が高いとすると、Vroom型の期待理論で第2次の結果(外的報酬)として動機づけ理論の中で位置づけられるべき給与や作業条件などが、実際には衛生要因にすぎなかったということになる。それに代わって見いだされた動機づけ要因について、Herzberg et al. (1959, p.114)は、仕事において自らの先天的潜在能力に応じて、現実の制限の内で、創造的でユニークな個人として自分の資質を十分に発揮したいという自己実現(self-actualization)の個人的欲求を満たすからこそ満足要因になるのだと主張している。こうしたことを明らかにしてくれるのが、内発的動機づけの理論である。
内発的に動機づけられた活動とは、Atkinson型のモデルのところでも触れたように、当該の活動以外には明白な報酬がまったくないような活動のことである。見た目には、つまり外的には何も報酬がないのに、その人がその活動それ自体から喜びを引き出しているようなとき、そう呼ばれる。Vroom型のモデルで考えられていたように、その活動が外的報酬に導いてくれる手段となっているからその活動に従事するのではない。その活動それ自体が目的となって、その活動に従事しているような活動を内発的に動機づけられた活動というのである(Deci, 1975, p.23 邦訳p.25)。
Deci (1975, p.61 邦訳p.68)はこの内発的動機づけ(intrinsic motivation)を考察し、「内発的に動機づけられた行動は、人がそれに従事することにより、自己を有能(competent)で自己決定的(self-determining)であると感知することのできるような行動」であると定義した。Atkinson (1957)の考えた達成動機づけも、環境との関係において自らが有能で自己決定的であることを感じたいという基本的な動機づけから分化したものであり、内発的動機づけの一つの特殊ケースとなる(Deci, 1975, p.107 邦訳p.120)。有能さと自己決定に対する内発的欲求は、出生時から既に存在しているのである(Deci, 1975, pp.82-84 邦訳pp.92-94)。(ここで、Maslowによる自己実現の欲求の位置づけとはその位置づけが根本的に異なっていることには十分な注意が必要である。Maslow (1943)は人間の欲求は最低次欲求から最高次欲求まで、
という順序で、階層的に配列されていると仮定した上で、低次の欲求は満足されると強度が減少し、欲求階層上の1段階上位の欲求の強度が増加するというように、欲求の満足化が低次欲求から高次欲求へと逐次的・段階的に移行していくという、いわゆる欲求階層説(need hierarchy theory)を主張し、そのときの最高次の欲求を自己実現の欲求とした(Maslow, 1943)。しかし、Maslowの欲求段階説に対しては、これまで数多くのさまざまな検証が試みられているものの、その試みはことごとく失敗していると言われ(Wahba & Bridwell, 1976)、Maslowの考えた自己実現の位置づけに科学的根拠はない。)
ここで有能さ(competence)の概念について説明を加えておこう。この概念は、もともとはWhite (1959)によるもので、日常的用法よりも広義に、生物学的意味で有機体がその環境と効果的に相互に作用する能力を指している。Whiteは広範な文献サーベイを行い、見る、つかむ、はう、歩く、考える、目新しいものや場所を探求する、環境に効果的な変化を生み出すといった行動は、それによって、動物や子供がその環境との間に効果的に相互に作用することを学習するプロセスを構成するという共通の生物学的意味をもっていると考えた。この共通の性質を指すために、有能さという用語が選ばれたのである。
つまり、自己の環境を処理し、効果的な「変化」を生み出すことができたとき、有能さを感じるのであり、DeciはWhiteの定義したこの有能さという用語を選ぶことで、変化性向の概念を考察していたことになる。人は自己の環境を自分で処理し、効果的な「変化」を生み出すことができるときに、有能であると感じるのであり、それはまさに自己決定的であると感じていることにほかならない(Deci, 1975, p.61 邦訳p.68)。そして、そうした有能さと自己決定(self-determination)の感覚に対する一般的欲求(Deci, 1975, p.62 邦訳p.70)こそが、個人の「変化」性向なのである。このように有能さはWhiteの定義まで遡れば、自己決定的であるということと同義になるが、有能さには日常の用法での意味が重ねられてしまうので、ここでは用いず、自己決定的という用語のみを用いることにしよう。
この変化性向がある程度の大きさでは存在しているために、人は、
という内発的に動機づけられた行動をとるのである(Deci, 1975, pp.61-63 邦訳pp.69-70)。そしてもし、ある人の自己決定の感覚が高くなれば、彼もしくは彼女の満足感は増加し、逆に、もし、自己決定の感覚が低くなれば、彼もしくは彼女の満足感は減少すると考えるのである(Deci, 1975, Proposition II)。
内発的動機づけの理論が正しければ、次の仮説が検証されてしかるべきである(高橋, 1993a, 仮説5(b))。
仮説8.1 (自己決定仮説). 組織の中での個人の自己決定の感覚が高いほど、職務満足感は高くなる。
この仮説の検証を行うためには、自己決定の感覚がなんらかの形で測定されなければならない。論理的にこれらを表す質問項目と考えられるものの中から、さらに高橋(1993a, ch.4)でも取り上げられているような主成分分析の結果も検討しながら絞り込みを行って、次の5問が選ばれた。
| D1 | トップの経営方針と自分の仕事との関係を考えながら仕事をしている。 |
| D2 | 上司からの権限委譲がなされている。 |
| D3 | 自分の意見が尊重されていると思う。 |
| D4 | 21世紀の自分の会社のあるべき姿を認識している。 |
| D5 | 良いと思ったことは、周囲を説得する自信がある。 |
これらの質問に、Yesならば1点、Noならば0点を与えて、ダミー変数化したうえで、5問を単純に加えた合計点を自己決定度(DINDEX)として定義することにしよう。自己決定度は0~5の整数値をとることができる。高橋(1993b)にしたがって、1990年、1991年、1992年の22社の調査データをもとにして仮説8.1の自己決定仮説を検証してみよう。これらの調査は、いずれも日本生産性本部の経営アカデミー『人間能力と組織開発』コースを舞台として8月末から9月初めにかけて行なわれた質問票調査である。このうち1990年の調査では、日本企業9社のホワイトカラー部門の正社員959人に対して9月5日~10日に質問票調査が行なわれ、853人から質問調査票が回収できた。回収率は88.9%であった。1991年の調査では、日本企業6社のホワイトカラー部門の正社員1017人に対して8月28日~9月2日に質問票調査が行なわれ、907人から質問調査票が回収できた。回収率は89.2%であった。1992年の調査では、日本企業7社のホワイトカラー部門の正社員847人に対して9月2日~7日に質問票調査が行なわれ、740人から質問調査票が回収できた。回収率は87.4%であった。
まず自己決定度の平均、標準偏差は表8.1のようになった。また、職務満足については、多元的概念で、しかもそれがどんな次元から構成されているのかについては、多くの研究者の間で必ずしも意見の一致はないとされているので(坂下, 1985, p.140)、ここでは次のYes-No二者択一形式の質問Q8.1で直接的に聞いてみることにする。
Q8.1 現在の職務に満足感を感じる。 1. Yes 2. No
この質問Q8.1でYesつまり満足感を感じると答えた人の比率を満足比率と呼ぶことにすると、表8.2、図8.2のように、自己決定度が上がるにつれて、満足比率もまた上昇するというようなきれいな直線的関係が得られる。図8.2の直線は回帰分析で求めたもので、その結果は表8.3に示されている。これによると、自己決定度3で満足比率はほぼ50%になり、自己決定度が1上がるごとに満足比率が約10%上昇する関係のあることがわかる。
表8.1 自己決定度
| 自己決定度 | ||||
|---|---|---|---|---|
| 会社数 | N | 平均 | 標準偏差 | |
| 1990年 | 9 | 831 | 2.72 | 1.66 |
| 1991年 | 6 | 889 | 3.22 | 1.46 |
| 1992年 | 7 | 716 | 2.77 | 1.46 |
| 全体 | 22 | 2436 | 2.92 | 1.55 |
表8.2 自己決定度と満足比率(1990~92年; N=2429)
| 質問Q8.1 職務満足 | 自己決定度 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 全体 | ||
| 1. Yes | 1990年 | 20 | 42 | 50 | 71 | 94 | 113 | 390 |
| 1991年 | 6 | 29 | 40 | 97 | 133 | 140 | 445 | |
| 1992年 | 8 | 32 | 51 | 74 | 80 | 86 | 331 | |
| 小計 | 34 | 103 | 141 | 242 | 307 | 339 | 1166 | |
| 2. No | 1990年 | 78 | 90 | 93 | 70 | 63 | 44 | 438 |
| 1991年 | 35 | 61 | 99 | 92 | 86 | 68 | 441 | |
| 1992年 | 40 | 67 | 110 | 98 | 47 | 22 | 384 | |
| 小計 | 153 | 218 | 302 | 260 | 196 | 134 | 1263 | |
| 全体 | 187 | 321 | 443 | 502 | 503 | 473 | 2429 | |
| 満足比率 | 18.18 | 32.09 | 31.83 | 48.21 | 61.03 | 71.67 | 48.00 | |
図8.2 自己決定度と満足比率(1990~92年)
表8.3 満足比率を被説明変数とする回帰分析(1990~92年)
| 変数 | 回帰係数 | 標準誤差 | t | 有意確率 |
|---|---|---|---|---|
| 自己決定度 | 10.590 | 0.980 | 10.804 | p <0.001 |
| 定数 | 17.360 | 2.968 | 5.850 | p <0.01 |
既にモデルのところでも述べたように、Atkinson型のモデルでは、個人がより困難なことにチャレンジするように動機づけられるのに対して、Vroom型のモデルではできるだけ容易な道へと向かってしまう。実際、Vroom型のモデルでは、職務誘意性は作業者が外的報酬を獲得できる程度の仕事をする確率とは関係するかもしれないが、たいていの場合、作業者の潜在的可能性をはるかに下回る業績レベルで十分に外的報酬を獲得できるので、その場合、とても効率的に生産活動を行っているとはいいがたい。
実は、既に、Vroom自身が広範な調査研究のサーベイの結果を次のように発見としてまとめていた(Vroom, 1964, ch.8):
そして、これらの発見は、職務遂行が目的達成の手段であるばかりでなく、目的そのものでもあることを示しており、個人は職務遂行に対する外的に媒介された結果とは無関係に、効率的遂行からは満足を引き出し、非効率的遂行からは不満足を引き出すことを示唆しているとしたのである(Vroom, 1964, pp.266-267 邦訳pp.304-305)。
しかも、金銭や賞賛のような外的報酬はまさに「外的」存在である。たとえ満足をもたらすとしても、満足は報酬の後にやってくることになる。このように外的報酬には満足を後に押しやってしまう効果があるために、外的報酬が内発的動機づけを制約する大きな顕現性(salience)とインパクトをもっているということをDeci (1975, Proposition I)は主張している。実際、内発的動機づけと外的報酬による動機づけとは付加的関係にはないということが、多数の実験研究から実証されている(Deci, 1975, ch.5.)。これらの実験では、内発的動機づけの測度として、
を採用しているが(Deci, 1975, pp.148-149 邦訳pp.166-167)、どちらの測度であれ、多くの場合、外的報酬は内発的動機づけを低下させているのである。例えば、大学生に興味のもてるパズルを解かせたときに、金銭的報酬を与えた試験群の方が、金銭的報酬を与えなかった統制群よりも、1のパズルに費やした時間の量が減ってしまったことが報告されている。
つまり、人間は期待効用原理で想定しているように、外的報酬という賞金のために、くじを引くがごとく仕事をし、働いているわけではない。いかに精緻な理論であっても、期待効用原理で、人間の意思決定、特に動機づけを説明し尽くすことはできない。組織の中の日常的な意思決定が決定理論的な意味で合理的に行われているために、通常なかなか表に顔を出さないのであるが、われわれを仕事に動機づけているのは、決定理論的な意味での合理的な判断ばかりではないはずである。人間にとっての仕事は単にくじを引く以上の何かである。仕事によって成長し、仕事によって直接満足感を得る。たとえ決定理論的な合理性の限界をやや逸脱しようとも、人間はそんなチャレンジの機会を求めているのである。